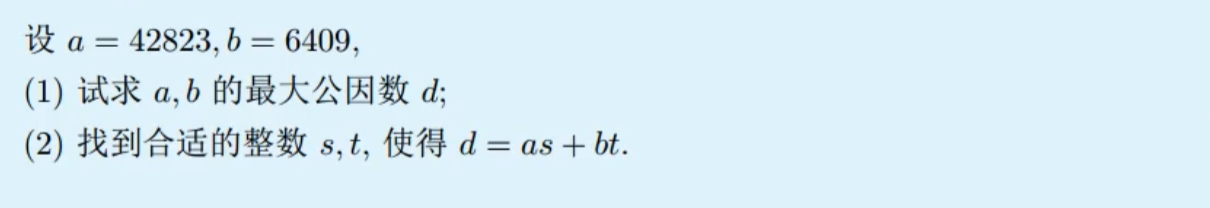数论基础

• 整除与带余除法是数论的基础，贯穿整个数论，对应教材初等数论闵嗣鹤第四版，学习课程是按照这本书来的

• 但是上图的书太薄了，如果是硬看书的话还是看国外的这本书

• 对于个人的博客，顺序按照个人认为比较合理的顺序进行排序。

整除和带余除法

整除

• 这里先介绍一下整除的定义，然后一些整除的命题和定理也进行归纳。

定义：

• 先介绍一下整除的定义：

$$\begin{array}{l} 设a，b∈Z，且b≠0。\\ 若存在q∈Z，有a = qb，则称b是a的因数（或约数），或a是b的倍数，或b能整除a，或a能被b整除。记作b|a。 \\若对任意的q∈Z，有a≠qb，则称a不能被b整除，记作b∤a。 \end{array}$$

命题：

命题1：

$$\begin{array}{l} 设a，b∈Z，且b≠0，则有：\\ 1.~~ b|0 (即零是任何非零整数的倍数)\\ 2.~~1|a (即1是任何整数的因数)\\ 3. ~~当a≠0时，a|a (任何一个非0整数都是它自身的因数) \end{array}$$

命题2：

$$\begin{array}{l} 设a，b，s∈Z\\ 1. ~~若b|a，则b|as。\\ 2. ~~b|a当且仅当 -b|a~~(即a的因数总是成对出现)。\\ 3. ~~b|a当且仅当 b||a|~~(即a与|a|的所有因数相同)。 \end{array}$$

命题3：

$$\begin{array}{l} 1. ~~若c|a，c∤b，则c∤(a+b)或c∤(a-b)\\ 2. ~~若b|a，c≠0，则bc|ac，反之若bc|ac，则b|a\\ 3. ~~若b|a，c|d则bc|ad\\ 4. ~~若a=b+c，d|a，d|b，则d|c \end{array}$$

命题4：

$$\begin{array}{l} 1.若n是正整数,a≠b,则a-b|(a^n-b^n)\\ 2.若n是正奇数,a≠-b,则a+b|(a^n+b^n)\\ 3.若n是正偶数，a≠-b,则a+b|(a^n-b^n) \end{array}$$

命题5（重要）：

(a,b)表示a,b两个数的最大公因数，[a,b]表示a,b两个数的最小公倍数。

对于命题5，这边先要介绍两个关于最小公倍数和最大公因数的定理。

定理1：注意这里的s、t可以是正的也可以是负的

$$已知(a,b)=x，则存在s,t∈Z,有sa+tb=x$$

定理2：

$$对于[a,b]和(a,b)，满足关系:[a,b] = \frac{ab}{(a,b)}$$

命题5如下：

$$\begin{array}{l} 1.若c\mid ab且(b,c) = 1，则c\mid a\\ 2.若b\mid a，c\mid a且(b，c)=1，则bc\mid a\\ 3.若b\mid a，c\mid a则[b，c]\mid a \end{array}$$

定理：

定理1(整除的传递性)：

$$设a，b，c∈Z，b，c≠0，则若b|a，c|b，则c|a。$$

定理2：

$$设a，b∈Z，都是m的倍数，则a+b或a-b也是m的倍数。$$

定理3：

$$设a_1,a_2,......,a_n∈Z都是m的倍数,q_1,q_2,......,q_n∈Z则q_1·a_1+q_2·a_2+......+q_n·a_n也是m的倍数 \\即若m|a_i(i=1,2,......,n),q_i∈z,则m|(q1·a1+......+q_n·a_n)$$

带余除法

• 带余除法的定义同时也是一个定理

• 所以这边先介绍一下带余除法的定义（定理）

$$设a，b∈Z且b＞0，则存在唯一的两个整数q和r，使得a=bq+r\\ 其中0≤r＜b$$

• 由这个定理可以得到一个推论即：这边将b>0替换成了b≠0

$$设a，b∈Z且b≠0，则存在唯一一对整数q和r，使得a=bq+r\\ 其中0≤r＜ \left | b \right |$$

在上面的定理和推论中，q叫做a被b除的不完全商，r叫做a被b除的余数。

最大公因数与辗转相除法

例题

• 在介绍最大公因数与辗转相除法之前，先来介绍一下最大公因数的求法

题目1：

​ 方法一：因数分解法

$$a=216=2^3*3^3\\ b=128=2^7\\ 所以(a,b)=2^3$$

​ 方法二：辗转相除法

$$216÷128=1···88\\ 128÷88=1···40\\ 88÷40=2···8\\ 40÷8=5···0\\ 所以最后(a,b)=8\\ \\ 还可以写成这样\\216=128*1+88 \\128=88*1+40 \\88=40*2+8 \\40=8*5+0 \\所以(a,b)=8$$

题目2：

​ 这题只能使用辗转相除法，因为这俩个数都是质数。

$$983=547*1+436\\ 547=436*1+111\\ 436=111*3+103\\ 111=103*1+8\\ 103=8*12+7\\ 8=7*1+1\\ 7=1*7+0\\ 所以(983,547)=1$$

题目3：

​ 这题同样使用两种方法

​ 方法1：

$$72=2^3*3^2\\ 48=2^4*3\\ 54=3^2*2*3\\ 所以(72,48,54)=6$$

​ 方法2：这题是3个数的最大公因数，使用辗转相除法，我们先要求其中俩个数的最大公因数，再将该数与第三个数求最大公因数。

$$72=48*1+24\\ 48=24*2+0\\ (72,48)=24\\ 54=24*2+6\\ 24=6*4+0\\ 所以(72,48,54)=6$$

最大公因数1

• 接下来介绍一下最大公因数的定义

定义1：

$$设整数a_1,a_2,...,a_n是n(n≥2)个整数\\ 如果整数d是它们中每一个因数,则称d为a_1,a_2,....a_n的公因数。\\$$

定义2：

$$整数a_1,a_2,...,a_n的公因数中最大的一个称为它们的最大公因数, \\记作(a_1,a_2,...,a_n).$$

定义3：

$$如果(a_1,a_2,...,a_n)=1,则称a_1,a_2,...,a_n互质或互素.\\ 如果a_1,a_2,...,a_n中任意两个整数互质，则称它们两两互质。$$

• 接下来是几个命题

命题1：该命题讨论的是公因数存在性问题。

$$\begin{array}{l} a_1,a_2,...,a_n∈Z的公因数必定存在\\ 若a_1,a_2,....,a_n不全为零,则(a_1,a_2,...a_n)必定存在.\\ 当a_1,a_2,....,a_n不全为零时,(a_1,a_2,...,a_n)>0 \end{array}$$

说明：

1. 该点说明，在理论证明的时候，我们只需要考虑不全为零的最大公因数
2. 在具体计算时，我们只考虑都不为零的整数的最大公因数
3. 两两互质蕴含互质，但反之不成立。

注解1：这个命题可以做为最大公因数的一个证明方法

$$\begin{array}{l} 设a_1,a_2,...,a_n为n个不全为零的整数，则(a_1,a_2,...,a_n)=d当且仅当\\ (1)d\mid a_i(i=1,2,...,n);\\ (2)若d' \mid a_i(i=1,2,...,n),则d'≤d. \end{array}$$

注解2：该注解也给出了最大公因数的一个证明方法，本质上该方法是注解1得到的。

$$\begin{array}{l} d=(a_1,a_2,...,a_n)当且仅当\\ (1)d\mid a_i(i=1,2,...,n);\\ (2)若d'\mid a_i(i=1,2,...,n),则d'\mid d(d>0) \end{array}$$

在证明d’=d时就可以利用d|d’,d’|d以及，d，d‘＞0，即可得到d=d’

命题2:

$$若b \mid a且a>0,则b≤a.$$

​ 通过这个命题，还有一个推论：

$$若b\mid a且a≠0,则\mid b \mid ≤ \mid a\mid$$

• 接下来给出最大公因数的几个性质定理：

定理1：由定理1就可以得到，如果要求一些数的公因数或者最大公因数，那么只要求这些数对应整数的公因数和最大公因数即可。

$$\begin{array}{l} 设a_1,a_2,...,a_n为n个不全为零的整数，则\\ (1)a_1,a_2,...,a_n与\left | a_1 \right |,\left | a_2 \right |,...,\left | a_n \right |的公因数相同。\\ (2)(a_1,a_2,...,a_n)=(\left | a_1 \right |,\left | a_2 \right |,...,\left | a_n \right |) \end{array}$$

定理2：

$$\begin{array}{l} 若b>0,且b∈Z，则:\\ (1)0与b的公因数就是b的因数，反之，b的因数也是0与b的公因数\\ (2)(0,b)=b \end{array}$$

定理2推论:

$$若b≠0,b∈Z，则(0,b)=\left | b \right |$$

辗转相除法

• 之前例题介绍了辗转相除法的具体过程，接下来介绍一下概念和具体定理。

定理3（延续最大公因数的定理1和定理2）:

$$设a,b,c是三个不全为零的整数，且a=bq+c(q≠0), 则a,b与b,c有相同的公因数,从而有(a,b)=(b,c)$$

定理4：在介绍定理4之前先具体说一下辗转相除法。

$$设a,b∈Z_+由带余除法：\\ a=bq_1+r_1 (0≤r_1<b).\\若r_1=0,则(a,b)=b,~~~~~若r_1≠0,则由定理3,(a,b)=(b,r1)\\ (r1≠0),b=r_1q_2+r_2(0≤r_2＜r_1)\\ 若r_2=0，则(a,b)=(b,r_1)=r_1,~~~~若r_2≠0,则由定理3,(a,b)=(b,r1)=(r_1,r_2) \\.........\\ r_{n-1}=r_nq_{n+1}+r_{n+1},~~~~~r_{n+1}=0 \\则(a,b)=(b,r_1)=...=(r_{n-1},r_n)=(r_n,r_{n+1})=(r_n,0)=r_n$$

从而引出定理4：

$$若a,b∈Z,则(a,b)=r_n$$

再利用最大公因数的定理1，就可以将该式子转换为

$$若a,b∈Z,则(a,b)=(\left | a \right |,\left | b \right |)=r_n$$

推论:

$$a,b的公因数与它们的最大公因数(a,b)具有相同的因数。$$

最大公因数2

• 接下来的定理就是一些最大公因数的运算性质了，这种运算性质可以进行抽象，抽象之后就是近世代数要研究的内容了。

定理5:定理5的运算性质就很想向量的内积的一些运算性质，可以进行类比记忆

$$\begin{array}{l} 设a,b是任意两个不全为零的整数，则\\ (1)若m∈Z_+，则(ma,mb)=m(a,b);\\ (2)若\delta是a，b的一个公因数，则(\frac{a}{\delta},\frac{b}{\delta} )=\frac{(a,b)}{\delta}\\ 特别地,(\frac{a}{(a,b)},\frac{b}{(a,b)})=1 \end{array}$$

注解4:

$$(a,b)=d当且仅当存在唯一的一对互质的整数，a_1,b_1使得a=da_1,b=db_1$$

定理6：就是例题中第3题所示的求三个数的最大公因数。由该定理就可以得到例题第3题的解法

$$\begin{array}{l} 设a_1,a_2,...,a_n是不全为零的整数(可以假定它们都是正整数)，且\\ (a_1,a_2)=d_2,~~(d_2,a_3)=d_3~~,...,~~(d_{n-2},a_{n-1})=d_{n-1},(d_{n-1},a_{n})=d_n,\\ 则(a_1,a_2,...,a_n)=d_n \end{array}$$

最大公因数3

• 这里介绍一下最大公因数的进一步的性质。先来介绍一个定理，该定理比较重要，由该定理可以导出著名的裴蜀定理。

定理1:

$$\begin{array}{l} 若a,b∈Z_+,则满足Q_ka-P_kb=(-1)^{k-1}r_k~~(k=1,2,...,n)\\ 其中\\ P_0=1,P_1=q_1,P_k=q_kP_{k-1}+P_{k-2}\\ Q_0=0,Q_1=1,Q_K=q_kQ_{k-1}+Q_{k-2}\\ (k=2,3,...,n) \end{array}$$

推论1:上面定理引出的该推论就是著名的裴蜀定理。该定理在之前的证明中有使用过。

$$\begin{array}{l} 若(a,b)=d,则存在s,t∈Z有as+bt=d. \end{array}$$

命题1:推理1的逆命题是不成立的，但是如果加了一些条件就会满足了。

$$\begin{array}{l} 设a,b,d∈Z，d>0,若存在s,t∈Z,有as+bt=d,且d是a,b的公因数,则(a,b)=d. \end{array}$$

推论2:

$$\begin{array}{l} 设a,b∈Z,则(a,b)=1,当且仅当存在s,t∈Z，有as+bt=1 \end{array}$$

定理2：

$$\begin{array}{l} 设a,b,c∈Z且(a,c)=1，则\\ (1)ab,c与b,c有相同的公因数\\ (2)(ab,c)=(b,c)\\ 这里b,c中至少有一个不为零 \end{array}$$

推论3：

$$\begin{array}{l} 若(a,b)=1,c\mid ab,则c\mid b \end{array}$$

推论4：

$$\begin{array}{l} 设a_1,a_2,...,a_n,b_1,b_2,...,b_m是两组整数\\ 如果前一组的任意一个数与后一组中任意一个都互质,则a_1a_2...a_n与b_1b_2...b_m互质 \end{array}$$

• 这里来个例题：

• 接下来介绍一下其他推论、定理和命题

最小公倍数

• 接下来介绍一下最小公倍数的定义和几个性质定理

定义：

$$\begin{array}{l} 若e是所有a_1,a_2,...,a_n的倍数，则称e为a_1,a_2,...,a_n的公倍数\\ 在所有公倍数中的最小正数,叫做a_1,a_2,...,a_n的最小公倍数,记为[a_1,a2,...,a_n] \end{array}$$

注解:由定义引出了证明最小公倍数的方法

$$\begin{array}{l} [a_1,a_2,...,a_n]=e当且仅当\\ (1)a_i\mid e(i=1,2,...,n);\\ (2)若a_i\mid e',则e≤e' \end{array}$$

定理1：

$$\begin{array}{l} [a_1,a_2,...,a_n]=[\left | a_1 \right |,\left | a_2 \right |,...,\left | a_n \right |] \end{array}$$

定理2：

$$\begin{array}{l} 设a,b∈Z_+,\\ (1)a,b的所有公倍数就是[a,b]的所有倍数;\\ (2)[a,b]= \frac{ab}{(a,b)},(或[a,b](a,b)=ab.)\\ 特别地,若(a,b)=1,则[a,b]=ab \end{array}$$

定理3：

$$\begin{array}{l} 若[a_1,a_2,a_3,...,a_n]=m,[a_1,a_2]=m_2,[m_2,a_3]=m_3,...[m_{n-1},a_n]=m_n,则m=m_n \end{array}$$

多项式带余除法

• 最小公倍数这边引出了多项式
• 下面给出多项式的定义并且引出多项式的带余除法

定义：

$$\begin{array}{l} 设n∈Z_+,a_0,a_1,...,a_n∈R,a_n≠0,则称\\ P(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\\ 为一个n次多项式，简称多项式。 \end{array}$$

多项式带余除法

$$\begin{array}{l} 设P(x),M(x)是任意两个多项式,P(x)的次数大于M(x)的次数,则存在唯一的一对多项式Q(x),R(x)使得 \\P(x)=M(x)Q(x)+R(x) \\其中R(x)的次数小于M(x)的次数 \end{array}$$

算数基本定理

质数和合数

• 质数和合数在数论中是非常重要的

定义1：质数和合数的定义：

$$\begin{array}{l} 设p是一个大于1的整数，若它的正因数只有1及它本身，\\则称p为一个质数(或素数),否则称为合数。 \end{array}$$

注1：负数、0和1既不是质数也不是合数。

推论1：

$$\begin{array}{l} a是合数当且仅当存在整数1<a_1,a_2<a,有a=a_1*a_2 \end{array}$$

• 介绍完定义后，接下来介绍一下质数和合数相关的定理

定理1：

$$\begin{array}{l} 设a是大于1的整数,则a的除1外的最小正因数p一定是质数,并且当a为合数时,p≤\sqrt{a} \end{array}$$

定理2：

$$\begin{array}{l} 设a∈Z,p是一个质数,则p \mid a或(p,a)=1 \end{array}$$

推论2：

$$\begin{array}{l} 设a_1,a_2,...,a_n∈Z,p是质数\\ 若p\mid a_1a_2....a_n,则p能整除某一个a_i \end{array}$$

算数基本定理

定理3：

$$\begin{array}{l} 任意大于1的整数都能表示为若干质数的乘积\\ 即若a>1,则a=p_1p_2...p_n,p1 \leq p_2 \leq ....\leq p_n,其中p_i都是质数 \end{array}$$

推论3：

$$\begin{array}{l} 设a是大于1的整数,则a能唯一地写为a=p^{\alpha_1}_1p_{2}^{\alpha_2}....p_i^{\alpha_i}....p_k^{\alpha_k} \\其中\alpha_i ＞0,i=1,2,3,...,k~且~p_i<p_j \\称上式为a的标准分解式. \end{array}$$

注解1：对于推论3，我们可以如下变形

$$\begin{array}{l} 在应用中,为方便计算，有时我们插进若干质数的零次幂,从而a可以表示为下面的形式\\ a = p_1^{\alpha_1}p_2^{\alpha_2}...p_l^{\alpha_l},\alpha_i \geq 0,i=1,2,3,...,l \end{array}$$

推论4：

$$\begin{array}{l} 设a是大于1的整数,且a=p^{\alpha_1}_1p_{2}^{\alpha_2}....p_i^{\alpha_i}....p_k^{\alpha_k},其中\alpha_i ＞0,i=1,2,3,...,k \\则a的正因数d可以表示为如下形式:\\d=p_1^{\beta_1}p_2^{\beta_2}...p_l^{\beta_k},0\leq \beta_i\leq \alpha_i，i=1,2,3,...,k \\而且当d可以表示成上述形式时,d是a的正因数 \end{array}$$

注解2：对于推论4，有如下结论

$$\begin{array}{l} 设a = p_1^{\alpha_1}p_2^{\alpha_2}...p_k^{\alpha_k},\alpha_i > 0,i=1,2,3,...,k,\\则a的正因数的个数有(\alpha_1+1)(\alpha_2+1)(\alpha_3+1)···(\alpha_k+1)个 \end{array}$$

取整函数[x]

• 先来了解一下取整函数的定义

定义：

$$\begin{array}{l} 设x∈R,定义[x]等于不超过x的最大整数,称函数[x]为取整函数或高斯函数. \\另外也称[x]为x的整数部分,\{x\}=x-[x]为x的小数部分 \end{array}$$

• 了解定义后对于取整函数有如下的基本性质

$$\begin{array}{l} 函数[x]，{x}具有下列性质: \\(1)~x = [x]+{x}; \\(2)~[x]≤x＜[x]+1,~~~x-1＜[x]≤x,~~~0≤\{x\}＜1; \\(3)~设n∈Z,则[n+x]=n+[x]; \\(4)~[x]+[y]≤[x+y],~~~\{x\}+\{y\}≥\{x+y\} \\(5)~~~~[-x] = \begin{cases} -[x]-1, & \text{if } x ∉ Z, \\ -[x], & \text{if } x ∈ Z. \end{cases} \\(6)~(带余除法)设a,b∈Z,b＞0,则\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~a=b[\frac{a}{b}]+b\{\frac{a}{b}\},0≤b\{\frac{a}{b}\}≤b-1 \\(7)~若a,b∈Z_+,则b的倍数中小于等于a的正整数的个数为[\frac{a}{b}]; \\(8)~若x≤y,则[x]≤[y]. \end{array}$$

• 现在来介绍一些相关定理,这些定理是可以用基本性质推导出来的。

定理1：

$$\begin{array}{l} 在n!的标准分解式中素因数p(p≤n)的指数h,有: \\~~~~~~~~~~~~~h=[\frac{n}{p}]+[\frac{n}{p^2}]+....=\sum_{r=1}^\infty[\frac{n}{p^r}] \end{array}$$

推论1：

$$\begin{array}{l} n!=\prod_{p≤m}p^{\sum_{r=1}^\infty[\frac{n}{p^r}]} \\其中\prod_{p≤n}表示展布在不超过n的一切素数上的乘积式. \end{array}$$

推论2：

$$\begin{array}{l} 贾宪数(组合数)\frac{n!}{k!(n-k)!}(0≤k≤n)是整数,记作C^k_n~或者记作\binom{n}{k} \end{array}$$

推论3：

$$\begin{array}{l} 若f(x)是一个n次整系数多项式,f^{(k)}(x)(k≤n)是它的k阶导数, \\则\frac{f^{(k)}(x)}{k!}是一个(n-k)次整系数多项式. \end{array}$$

定理2:

$$\begin{array}{l} 任何k个连续整数的乘积一定能被k!整除. \end{array}$$

不定方程

• 不定方程初高中都有接触过，接下来直接给出定义再给出几个例子。

定义1：不定方程

$$\begin{array}{l} 未知数必须受到某种限制(如整数,正整数或有理数等)的方程,称为不定方程 \end{array}$$

例子

$$\begin{array}{l} 例1:~~x^2+y^2=z^2,其中x,y,z是正整数这就是一个不定方程 \\例2:~~11x+5y=1028,其中x,y是整数,这样也就是一个不定方程 \end{array}$$

二元一次不定方程

• 了解了不定方程之后，接下来看二元一次不定方程的定义

定义2：二元一次不定方程

$$\begin{array}{l} 设a,b,c∈Z,ab\neq0，则称式子\\ ~~~~~~~~~~~~~~~~~ax+by=c\\ 为关于变量x,y的二元一次不定方程 \end{array}$$

• 了解了二元一次不定方程的概念之后，接下来一定是研究该方程如何解

定理1：二元一次不定方程的通解

$$\begin{array}{l} 设二元一次不定方程:~~ax+by=c(a,b,c∈Z,ab\neq0) \\有一整数解x=x_0,y=y_0,且(a,b)=d,~a=a_1d,~b=b_1d, \\则此不定方程的一切整数解可以表示为: \\x=x_0-b_1t,y=y_0+a_1t~~其中t∈Z \end{array}$$

注意：该定理中的(a1,b1)=1，具体参考最大公因数2的注解4

证明

• 证明这个定理需要证明两个地方：

$$\begin{array}{l} 证明第一个地方:\\x=x_0-b_1t,y=y_0+a_1t~~一定是ax+by=c的解 \\证明第二个地方:\\ ax+by=c的整数解,总可以表示成x=x_0-b_1t,y=y_0+a_1t \end{array}$$

• 证明过程如下：

$$\begin{array}{l} 证明1:将x=x_0-b_1t,y=y_0+a_1t代入ax+by=c可得\\ a(x_0-b_1t)+b(y_0+a_1t)\\ =ax_0-ab_1t+by_0+a_1bt \\ \because ax_0+by_0=c \\ \therefore ax_0-ab_1t+by_0+a_1bt=c-ab_1t+a_1bt \\又知道(a,b)=d,~a=a_1d,~b=b_1d \\ \therefore c-ab_1t+a_1bt\\=c+t(a_1b-ab_1) \\=c+t(a_1b_1d-a_1b_1d) \\=c \\ \therefore x=x_0-b_1t,y=y_0+a_1t~~一定是ax+by=c的解 \end{array}$$

$$\begin{array}{l} 证明2:设\begin{cases} x=x_1 \\ y=y_1 \end{cases} 是ax+by=c的任意一个整数解 \end{array}$$