椭圆曲线加密

• 参考博客：ECC椭圆曲线详解(有具体实例) - Yumeka - 博客园 (cnblogs.com)
• [ECC椭圆曲线加密算法—加解密（SageMath实现） - lnjoy - 博客园 (cnblogs.com)](https://www.cnblogs.com/lnjoy/p/ecc.html#:~:text=简介. ECC椭圆曲)
• 椭圆曲线 (sagemath.org)
• 椭圆曲线 - 杰哥的知识库

前言

• 椭圆曲线，英文名称为Elliptic Curve。是代数几何中的一种曲线，椭圆曲线常用于现代密码学。

• 椭圆曲线加密，英文名称为Elliptic Curve Cryptography，才是我们经常所的ECC。

• 以下为几个常见的椭圆曲线加密的实际应用：

  • ECDH，即椭圆曲线迪菲-赫尔曼密钥交换
  • ECDSA，即椭圆曲线数字签名算法
  • ECIES，椭圆曲线集成加密方案
  • Elliptic Curve PGP，即椭圆曲线PGP加密
  • 在比特币和区块链中也使用ECC

• 这里先来介绍几个椭圆曲线的常见型式。椭圆曲线方程常见的型式有：Weierstrass标准方程、Montgomery曲线、Edwards曲线。其中Weierstrass标准方程是椭圆曲线中加密的最常见的方程型式。接下来逐个介绍一下这些方程的型式。

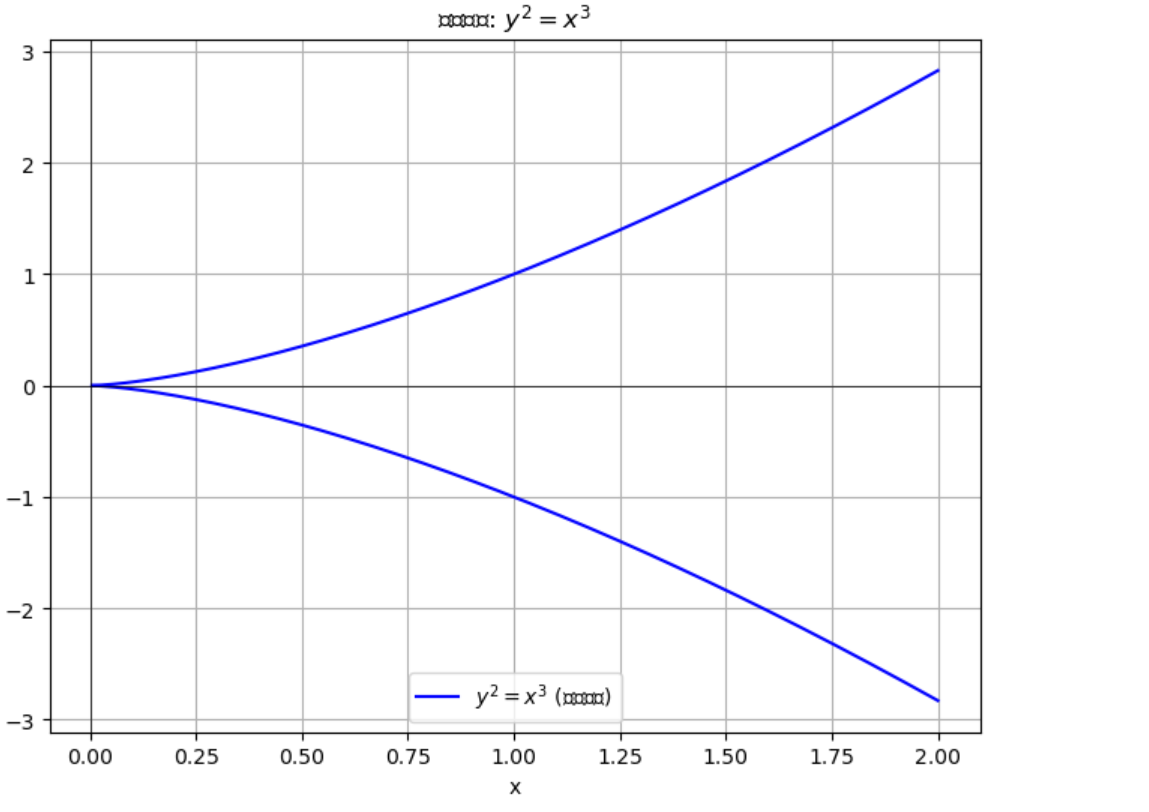
型式1(Weierstrass标准方程——简化形式)：

$$\begin{array}{l} 椭圆曲线的标准方程型式如下:\\ y^2=x^3+ax+b\\ 其中：\\ x和y是椭圆曲线上的点坐标\\ a和b是定义椭圆曲线的常数,且该常数要满足条件:4a^3+27b^2≠0\\ 即这个条件确保曲线没有奇点(如尖点或自交点) \end{array}$$

型式2(Montgomery曲线)：

$$\begin{array}{l} 该曲线的形式如下:\\ By^2=x^3+Ax^2+x \end{array}$$

型式3(Edwards曲线)：

$$\begin{array}{l} x^2+y^2=1+dx^2y^2 \end{array}$$

椭圆曲线基础

• 虽然椭圆曲线有椭圆两个字，但是和椭圆的关系并不大，所以这里就不多介绍椭圆。

椭圆曲线的定义

• 椭圆的定义是采用Weierstrass标准方程定义的
• 定义如下：

$$\begin{array}{l} 在\mathbb{R}^2上的曲线(即在平面上的曲线)，曲线上每一点(x,y)满足:\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y^2=x^3+ax+b\\ 要求4a^3+27b^2≠0，这种型式叫做Weierstrass型式 \\该型式的齐次方程为:\\ ~~~~~~Y^2Z+a_1XYZ+a_3YZ^2=X^3+a_2X^2Z+a_4XZ^2+a_6Z^3 \end{array}$$

椭圆曲线上的运算

• 我们在椭圆曲线上定义了加法运算、乘法运算。首先要明白，这个运算并不是数与数的加法运算，而是椭圆曲线上的点的加法运算。

• 椭圆曲线上的点有一个比较奇特的地方，就是经过一些操作，椭圆曲线上的点满足群的运算性质。即满足群的定义：封闭性、结合律、单位元、逆元（如果是没有学过一点抽像代数就比较难理解，这就好比人为自定义的一个运算，比如小学我们学习乘法，3个相同的数相加就可以表示为这个数乘3，所以椭圆曲线上的加法运算、乘法运算只是人为定义，并且满足一定性质的运算。）

• 接下来介绍一下我们是如何定义椭圆的上的加法等运算。这里先用一个比较直观的椭圆曲线去理解椭圆曲线的上定义的运算。

运算过程

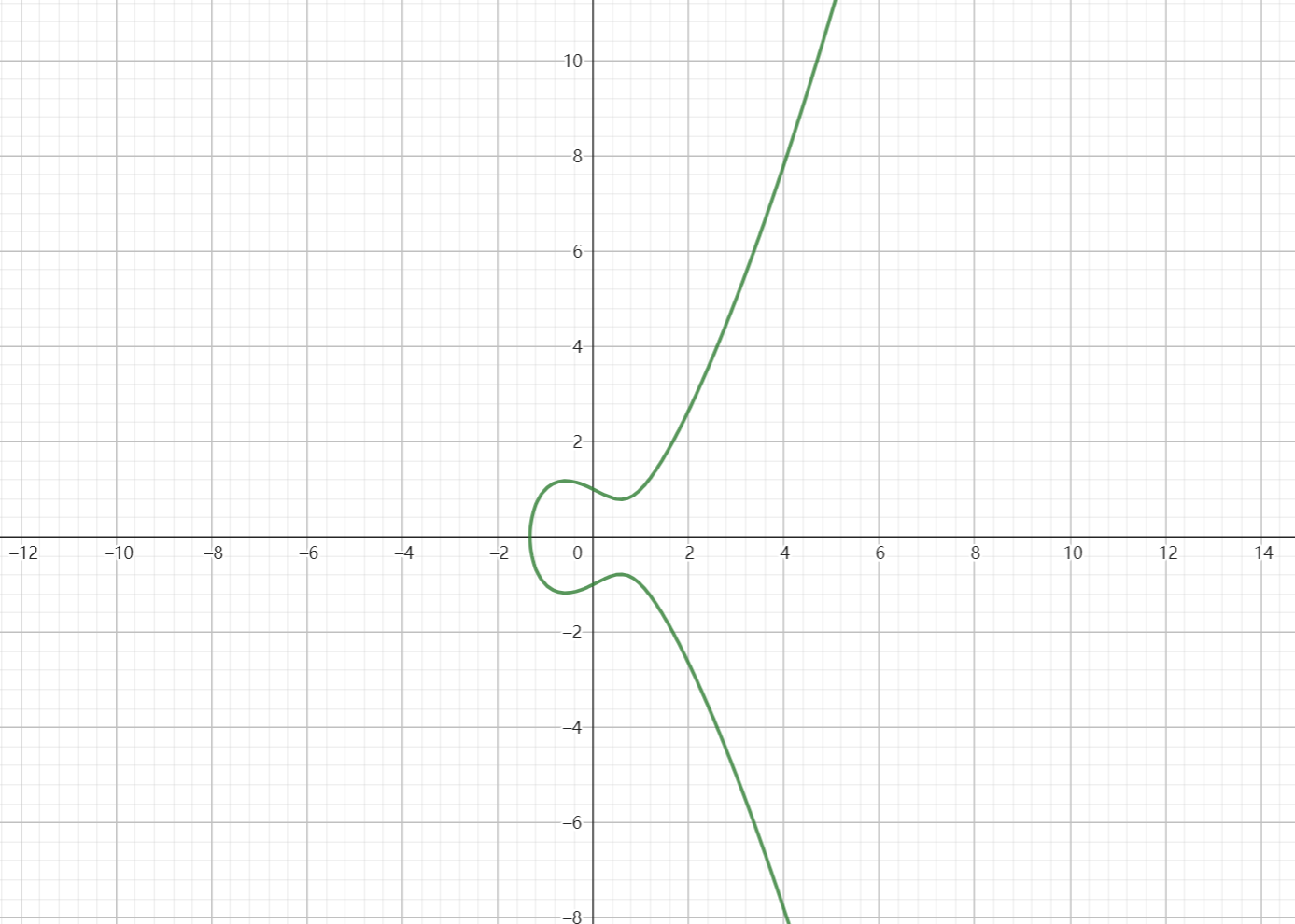
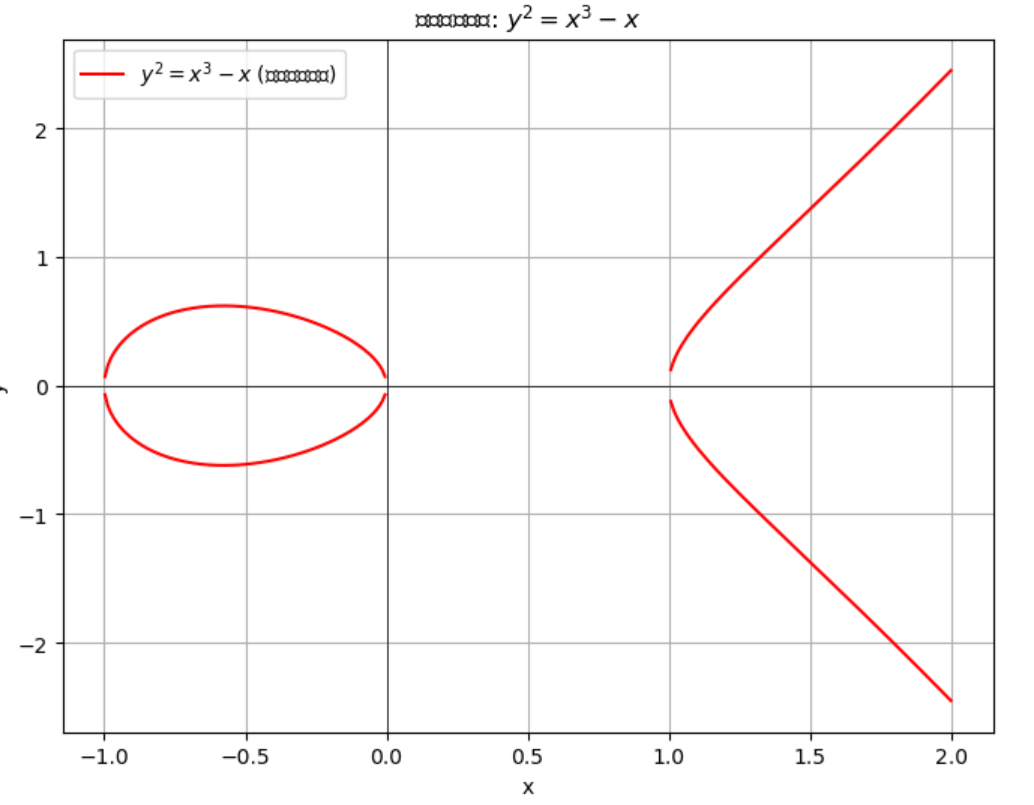
• 这边使用了GeoGebra画出了没有奇点的椭圆曲线，该椭圆曲线的方程和图像如下：

$$y^{2}=x^3-x+1$$

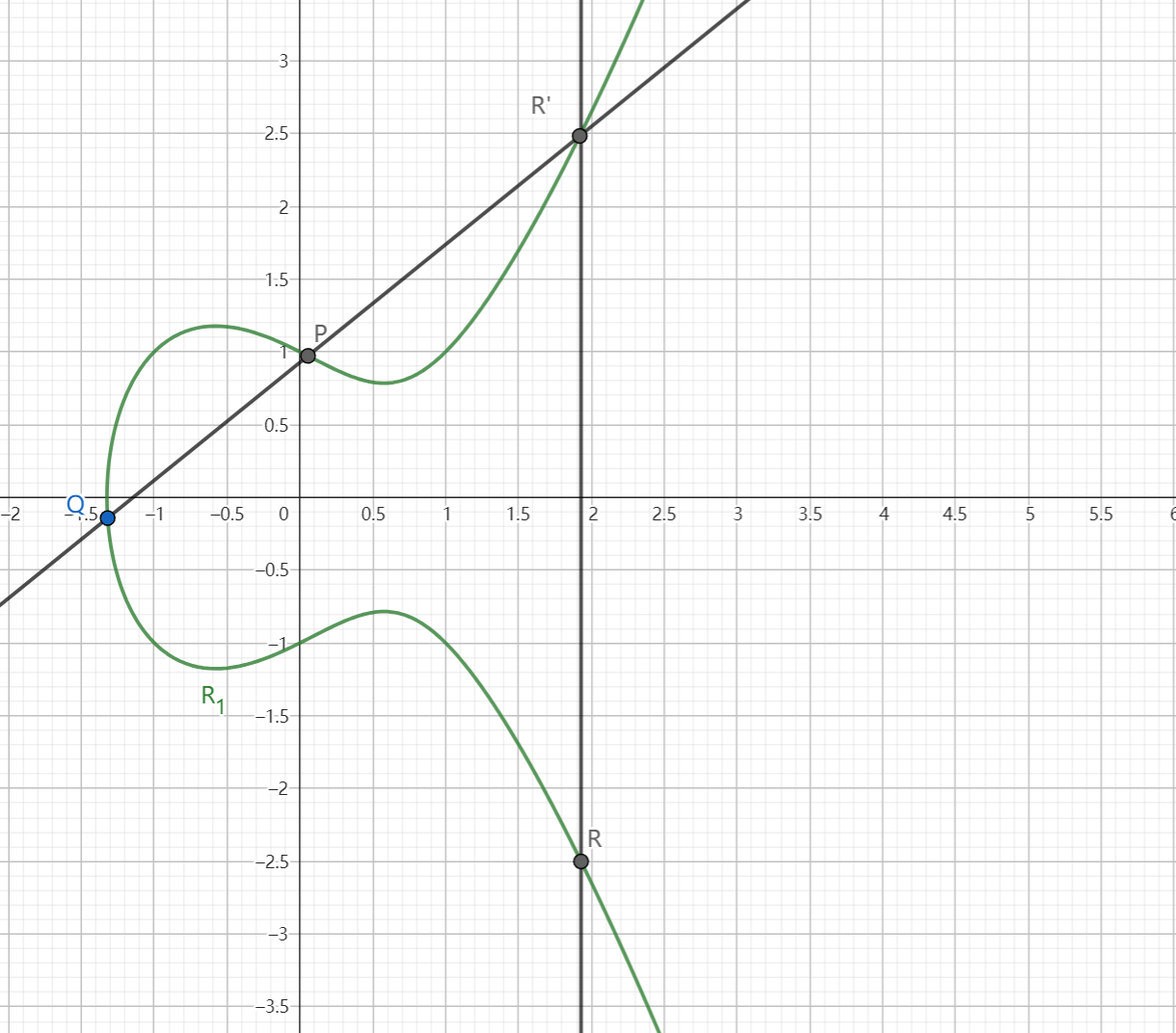
• 我现在任意取椭圆曲线上的两点P、Q(若P、Q两点重合，则作P点的切线)，作直线交于椭圆曲线的另一点R'，过R'做y轴的平行线交椭圆曲线于R，则我们定义P+Q=R。这就是椭圆曲线上的加法，并且这个加法同样满足交换律、结合律，即P+Q=Q+P=R,(P+Q)+C=P+(Q+C)=D。具体加法过程如下图所示：

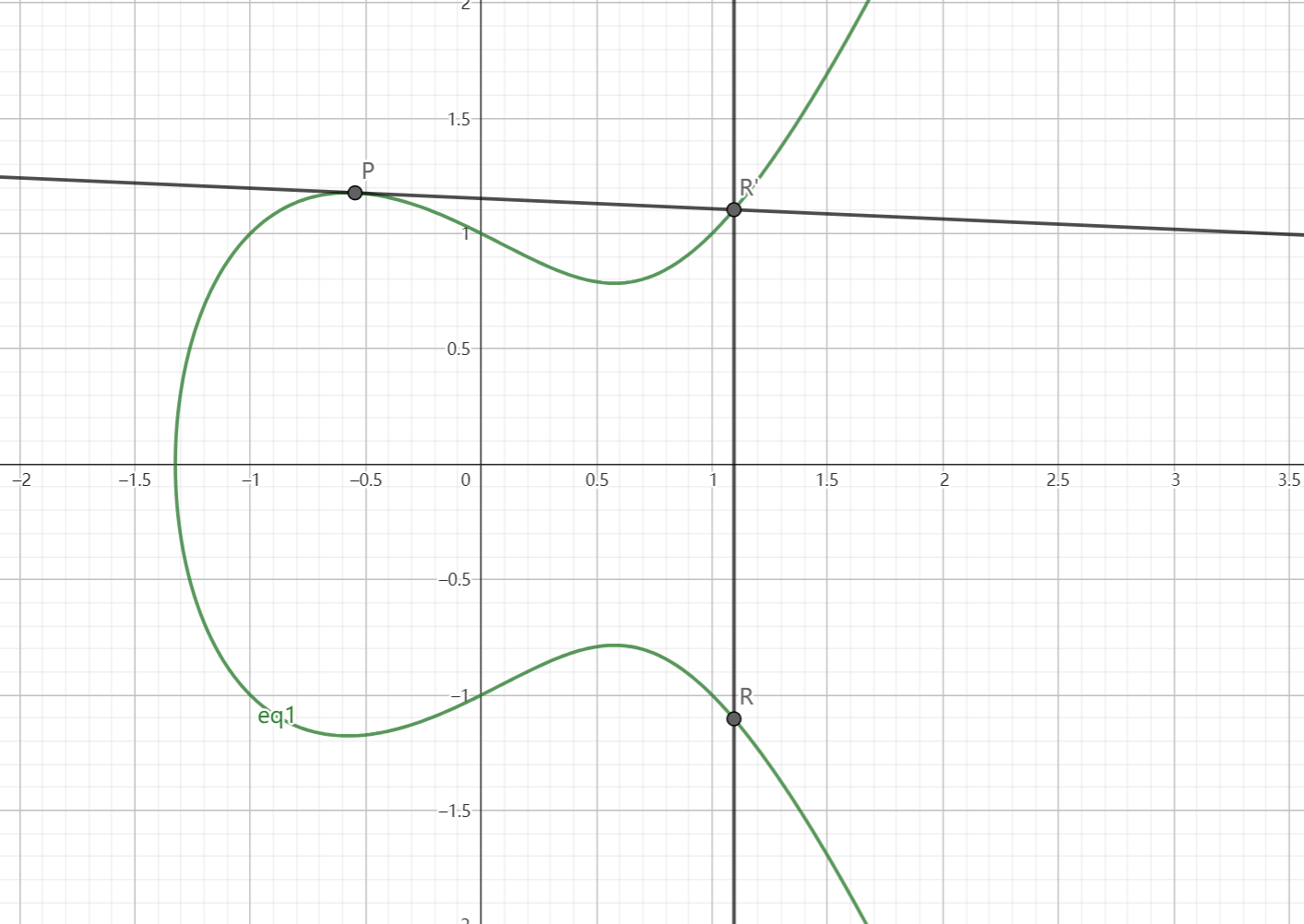
• 上图介绍了椭圆曲线的加法，接下来介绍一下椭圆曲线的乘法，假设P是椭圆曲线上的一个点，则椭圆曲线上的2P=P+P即，当上图的Q与P重合的时候，过点P做切线，然后交椭圆曲线为另一个点R'，过R'做y轴的平行线，交椭圆曲线为R则R这个点就是P+P=R的结果，下面为具体的图片

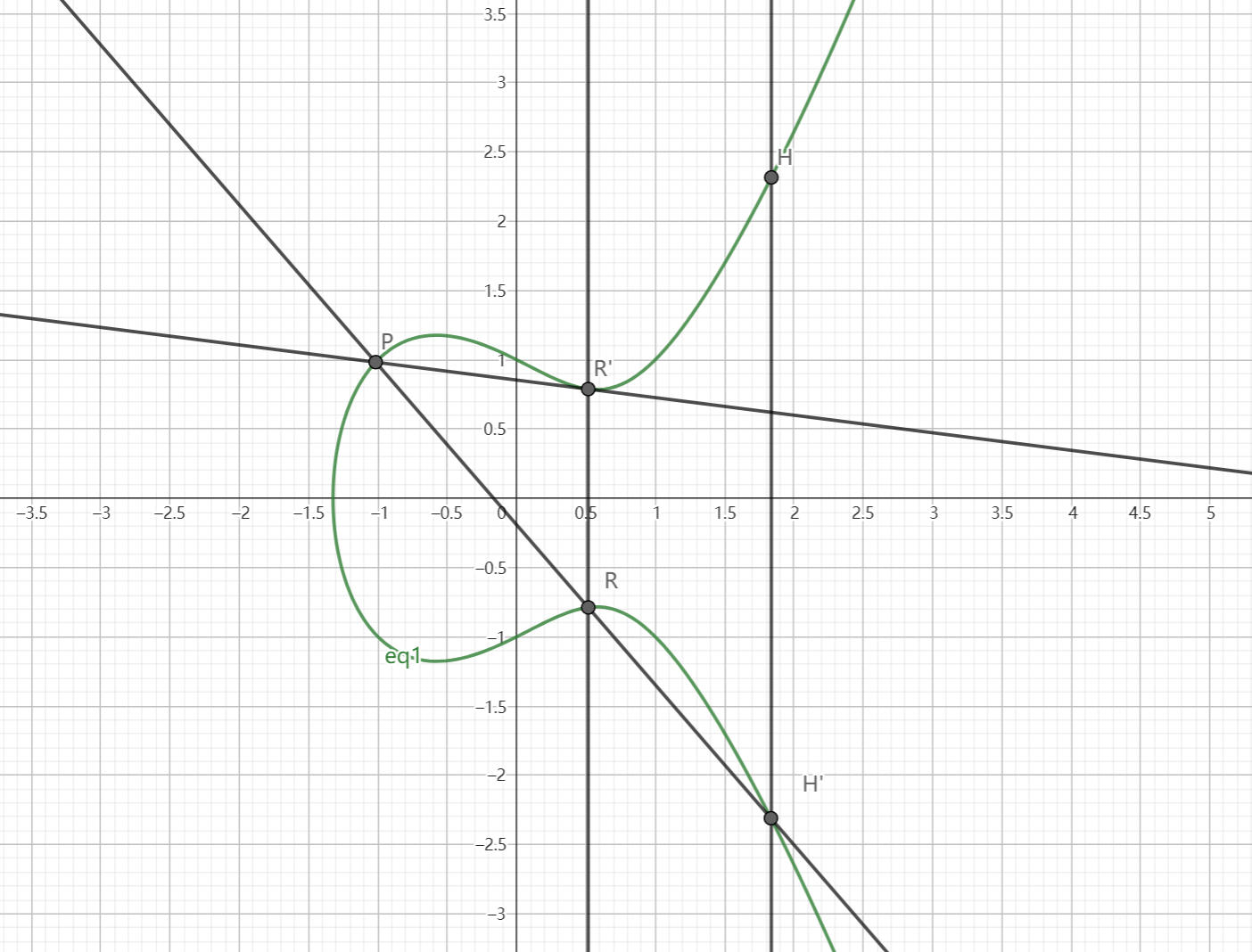
• 这样我们就可以引出3P的运算，3P=P+P+P=2P+P。
  • 所以我们就可以先求得2P的结果即点R
  • 然后我们再过点P和R做一条直线，交椭圆曲线为另一个点H'
  • 最后过H'做y轴的平行线，该平行线交椭圆曲线为H点，H点即为所求。
  • 具体图像如下图所示,图中的H点即为所求，即3P=H

运算定义

• 举了个实例后就可以更明白椭圆曲线的加法和乘法运算了。
• 接下来就具体说明一下椭圆曲线的加法的定义：

$$\begin{array}{l} 在椭圆曲线上，可以定义点之间的加法运算，满足: \\(1)单位元O为无穷点 \\(2)对于曲线上两点P和Q,取经过P和Q的直线，这条直线与椭圆曲线相交于最多三个点，\\其中两个点是P和Q， 如果第三个点存在且不和P、Q重合，记第三个点为R,\\那么满足P+Q+R=O，也就是P+Q=-R \\(3)对一点R=(x_p,y_p),其相反数-R=(x_p,-y_p),也就是沿X轴对称的点 \end{array}$$

有限域椭圆曲线

• 椭圆曲线是连续的，这并不适合加密。而通过上面的运算可以知道，对X、Y坐标的计算只涉及到了加减乘。所以可以把其坐标换到其他域上。
• 所以我们把椭圆曲线定义在有限域上。对于有限域，如果没有学抽象代数的话也并不是很理解有限域，对于有限域上的椭圆曲线，简单的理解为对椭圆曲线方程进行模运算。这里也给出有限域椭圆曲线的定义。

$$\begin{array}{l} 在有限域上，椭圆曲线的定义通常是给定一个特定的有限域\mathbb{F}_q和一个椭圆曲线标准方程\\ 对于有限域\mathbb{F}_q上的椭圆曲线,方程通常具有如下形式:\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y^2\equiv x^3 + ax+b(mod~q~)\\ 其中:\\ (1)a和b是给定的常数属于\mathbb{F}_q\\ (2)x和y是椭圆曲线上的点的坐标,它们的值属于有限域\mathbb{F}_q\\ (3)q是有限域的阶数,通常为素数p或素数的幂p^n \end{array}$$

注意：从有限域椭圆曲线的定义中可以得到x、y、a、b的取值只能在模数q的范围之内，且是一个正数。

• 下图是我生成的一个有限域上椭圆曲线的图像，该有限域椭圆曲线的图像和方程如下：

$$\begin{array}{l} y^2\equiv x^3 -x+1(mod~101~) \end{array}$$

• 从上方我们就可以发现，我们把之前连续的椭圆曲线，通过限制有限域，将图像变成离散。这样就更有利于加密，使得密文更不容易破解。

有限域上椭圆曲线的运算

• 有限域上椭圆曲线的运算其实和正常的椭圆曲线上的运算差别不大，只是多了一个取模的步骤。

(补充)特殊椭圆曲线图像

• 这时其中一种不平滑的椭圆曲线，这种椭圆曲线是奇异的

• 这是第二种奇异的椭圆曲线图，这里被挖掉了几个点

sage与椭圆曲线

• 在sage中有与椭圆曲线相关的类·，而在Python中没有，接下来就来介绍一下sage如何定义椭圆曲线和对椭圆曲线进行运算。

• 在sage中sage.schemes.elliptic_curves.constructor.EllipticCurveFactory中有定义椭圆曲线类。

• 在sage中的椭圆曲线方程默认为Weierstrass标准方程，即

$$y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$$

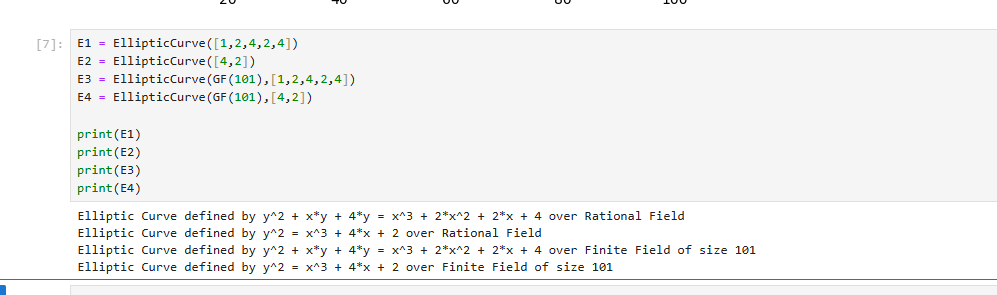
创建椭圆曲线类

• 我们可以使用EllipticCurve([a1,a2,a3,a4,a6])，定义一个正常的椭圆曲线。
• 我们还可以这样定义EllipticCurve([a4,a6])，定义一个a1,a2,a3都为0的椭圆曲线。
• 我们还可以使用EllipticCurve(GF(p),[a4,a6])或EllipticCurve(GF(p),[a,1,a2,a3,a4,a6])来定义一个有限域上的椭圆曲线，其中GF(p)一个有限域Fp

椭圆曲线点相关

• 椭圆曲线加密的是基于点的运算，所以ECC加密中，点的运算是很重要的。所以sage中椭圆曲线类也有相关方法去对椭圆曲线上的点进行操作

椭圆曲线加密

ECC保密通信算法

• A选定椭圆曲线E，并取椭圆曲线上的一点G作为基点
• A再选择一个私有密钥p，并生成公钥K=pG
• 然后A将椭圆曲线E、公钥K、基点G都传给B，自己则保留一个私钥p

from Crypto.Util.number import *
p = getPrime(256)
a = getPrime(256)
b = getPrime(256)
E = EllipticCurve(GF(p),[a,b])# 定义一个有限域上的椭圆曲线
G = E.random_point()          # 在该有限域上的椭圆曲线随机生成一个基点G
d = getPrime(256)             # 生成私钥
K = d*G                       # 生成公钥
print("有限域上的椭圆曲线方程为:",E)
print("私钥为:",d)
print("公钥为:",K)
print("基点为:",G)
"""
有限域上的椭圆曲线方程为: Elliptic Curve defined by y^2 = x^3 + 34074834305188571141621784296213127818605719682511236882697040475349160662918*x + 63132765410951845376834020294406549474122314748305927686818130532536873941891 over Finite Field of size 81030663492019274685634371044174577656868933015941657714008669865992779042659
私钥为: 99810097591477275848902367520793650692915987115714414713302591310302269523321
公钥为: (80717954411716455917392752597469377265534463105017126347424985504514145340030 : 14147750910960321057471889563638948577248840688236726694878310015967182371744 : 1)
基点为: (41277325230094923827769782781870562338415098379333818899654876460813430152803 : 33183583264342591073816729856317076097935781827230667008430557415668571274778 : 1)
"""

• B收到椭圆曲线E、公钥K、基点G后，先将消息M编码到椭圆曲线上一点M上，这个编码有很多种
• B这边还要生成一个随机数r
• B生成随机数后，计算C1 = M+r*K，C2=r*G
• B再将C1和C2传给A
• 这样A在收到B给的C1和C2就可以利用式子计算出M，M=C1-p*C2，数学推导过程如下

$$\begin{array}{l} C_1 = M+r*K\\ K=p*G\\ 所以有:C_1=M+r*p*G \\又已知:C_2=r*G \\所以:p*C_2=p*r*G \\所以:M=C_1-p*C_2 \end{array}$$

from Crypto.Util.number import *
flag = b'flag{you_know_yixixi}'
p = 81030663492019274685634371044174577656868933015941657714008669865992779042659
a = 34074834305188571141621784296213127818605719682511236882697040475349160662918
b = 63132765410951845376834020294406549474122314748305927686818130532536873941891
E = EllipticCurve(GF(p),[a,b])
G = (41277325230094923827769782781870562338415098379333818899654876460813430152803,33183583264342591073816729856317076097935781827230667008430557415668571274778)
G = E(G)
M1 = bytes_to_long(flag[:len(flag)//2])
M2 = bytes_to_long(flag[len(flag)//2:])
M = (M1,M2)          # 将消息编码到平面上一个点
K = (80717954411716455917392752597469377265534463105017126347424985504514145340030,14147750910960321057471889563638948577248840688236726694878310015967182371744)
# 使用公钥
G = E(G)
K = E(K)
r = getPrime(256) # 生成随机数r
print(r)
C1 = M[0]*G+r*K # 计算C1
C2 = M[1]*G+r*K # 计算C2
C3 = r*G   # 计算C3
print(C1)
print(C2)
print(C3)
"""
65964405526157595714499022295389061886508913366432486863319174824978859701519
(69151207374963881506229419807414044606562589019128390449154463436113810170056 : 34212945283157084946826868040823333490762807263420338368084079939026517093747 : 1)
(20052133424534836327031887427641190087578911424005778789411093448513364175045 : 79290733772592920486937801634073957445824487251333206942425193951959204643346 : 1)
(13873839514926178929123206541508951197152950503924156547704705249810871181474 : 16649925998290493656119874109251230518218117755115487436290837089158719083016 : 1)
"""

• 然后进行解密过程,由于映射方式选取的并不是特别好，所以最后解密只能使用爆破来得到明文。椭圆曲线对消息的不同映射对消息最后的恢复可能稍微有点影响。

from Crypto.Util.number import *
import libnum
p = 81030663492019274685634371044174577656868933015941657714008669865992779042659
a = 34074834305188571141621784296213127818605719682511236882697040475349160662918
b = 63132765410951845376834020294406549474122314748305927686818130532536873941891
E = EllipticCurve(GF(p),[a,b])
G = (41277325230094923827769782781870562338415098379333818899654876460813430152803,33183583264342591073816729856317076097935781827230667008430557415668571274778)
G = E(G)
d = 99810097591477275848902367520793650692915987115714414713302591310302269523321
C1 = (69151207374963881506229419807414044606562589019128390449154463436113810170056,34212945283157084946826868040823333490762807263420338368084079939026517093747)
C2 = (20052133424534836327031887427641190087578911424005778789411093448513364175045,79290733772592920486937801634073957445824487251333206942425193951959204643346)
C3 = (13873839514926178929123206541508951197152950503924156547704705249810871181474,16649925998290493656119874109251230518218117755115487436290837089158719083016)
C1 = E(C1)
C2 = E(C2)
C3 = E(C3)
D1 = C1 - p * C3
D2 = C2 - p * C3
for i in range(1,2**10):
    if a == D1:
        M1 = i
    if a == D2:
        M2 = i
print(libnum.n2s(int(M1)))
print(libnum.n2s(int(M2)))
"""
b'flag{you_k'
b'now_yixixi}'
"""

椭圆曲线题目

ECC_level_1

• 题目来源：攻防世界

已知椭圆曲线加密Ep(a,b)参数为
p = 15424654874903
a = 16546484
b = 4548674875
G(6478678675,5636379357093)
私钥为
k = 546768
求公钥K(x,y)
flag格式为cyberpeace{x+y的值}

• 了解了一下ECC保密通信算法，就可以知道公钥的值，直接使用sage跑出结果

p = 15424654874903
a = 16546484
b = 4548674875
E = EllipticCurve(GF(p),[a,b])
G = (6478678675,5636379357093)
G = E(G)
k = 546768
K = k*G
print(K)
a = 13957031351290
b = 5520194834100
a = a + b
print("cyberpeace{"+str(a)+"}")