高数下第八章
向量代数与空间解析几何
注:知识点的一些资料来源于网络,由于手打费时,而我做笔记主要是归纳题型,理清解题思路等等,敲知识点太慢了,就上网找了
向量及其线性运算
向量的概念
-
既有大小也有方向的量叫做向量‘。数学上通常用有向线段表示向量。
-
两个向量相等,它们的大小相等,且方向相同
-
-
-
-
单位向量:模等于1的向量是单位向量
向量的线性运算
向量加法
-
向量的加减法:三角形法则、平行四边形法则
-
-
向量数乘
- 向量数乘性质:结合律、分配律
- 两向量平行的充分必要条件
空间直角坐标系
- 看书没啥好记的
利用坐标向量的线性运算
- 空间向量坐标加减法
- 空间向量平行坐标对应成比例
- 向量的定比分点公式
向量的模、方向角、投影
- 有些是高中知识,但是有些符号定义与高中不一样

 3. 向量的投影
3. 向量的投影
- 投影的定义


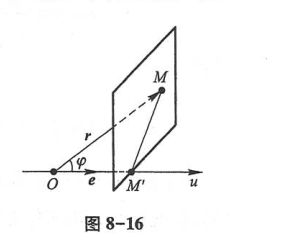
- 投影的性质

数量积 向量积 混合积
两向量的数量积
两向量的向量积

例题:


平面及其方程
- 平面的概念看一看
平面方程
- 点法式方程
- 一般式方程
- 截距式方程


两平面的夹角

平面束
- **定义:**空间中通过同一直线的所有平面的集合叫做有轴平面束,那条直线叫做平面束的轴
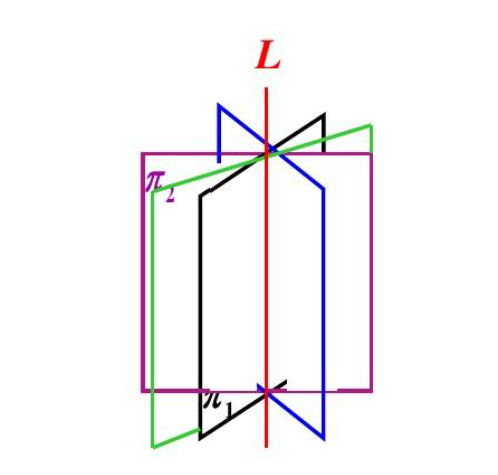
已知两平面\\ A_1x+B_1y+C_1z+D_1=0 \\A_2x+B_2y+C_2Z+D_2=0 \\相交于交线l
过l的平面束就可以表示为\\ A_1x+B_1y+C_1z+D_1+\lambda(A_2x+B_2y+C_2Z+D_2)=0\\ 注意:这里的平面束缺少平面A_2x+B_2y+C_2Z+D_2=0
空间直线及其方程
空间直线的方程
- 空间直线的一般方程
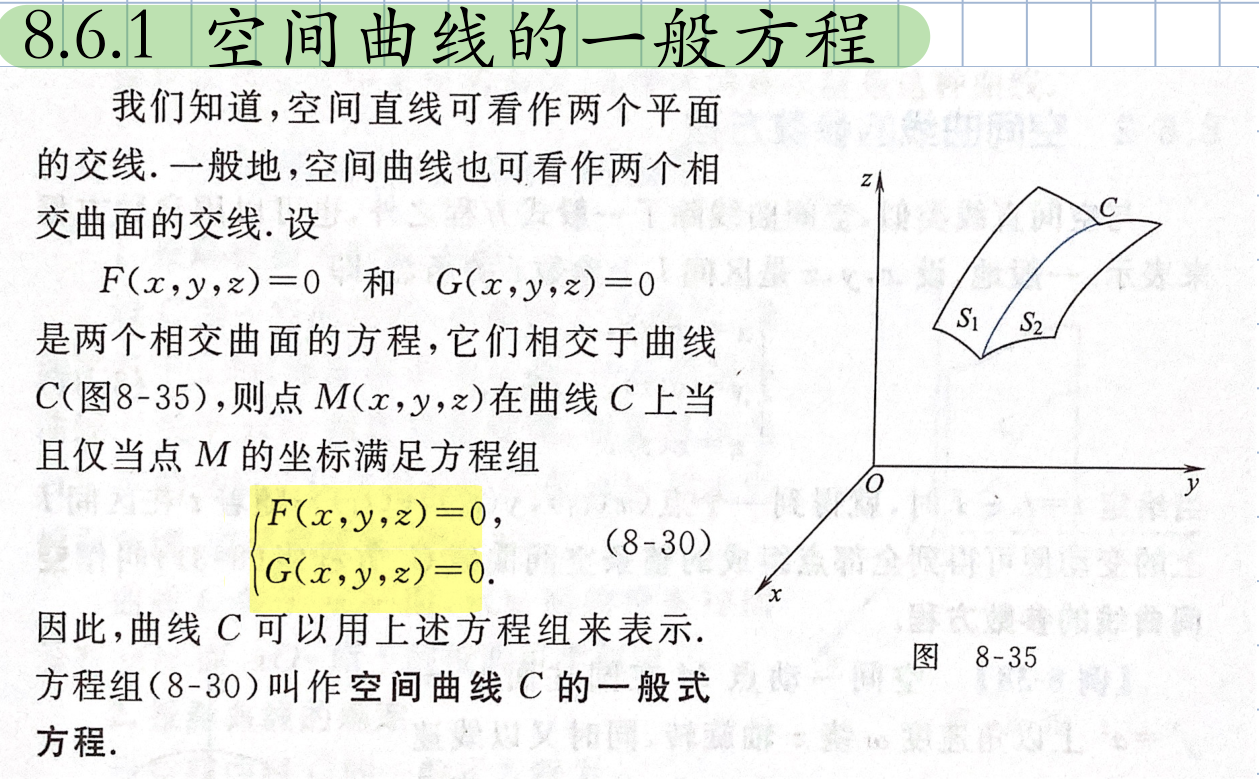
直线l可看成两平面的交线,则方程为:
- 对称式方程
- 参数方程
有
两直线的夹角

直线与平面的夹角

曲面及其方程

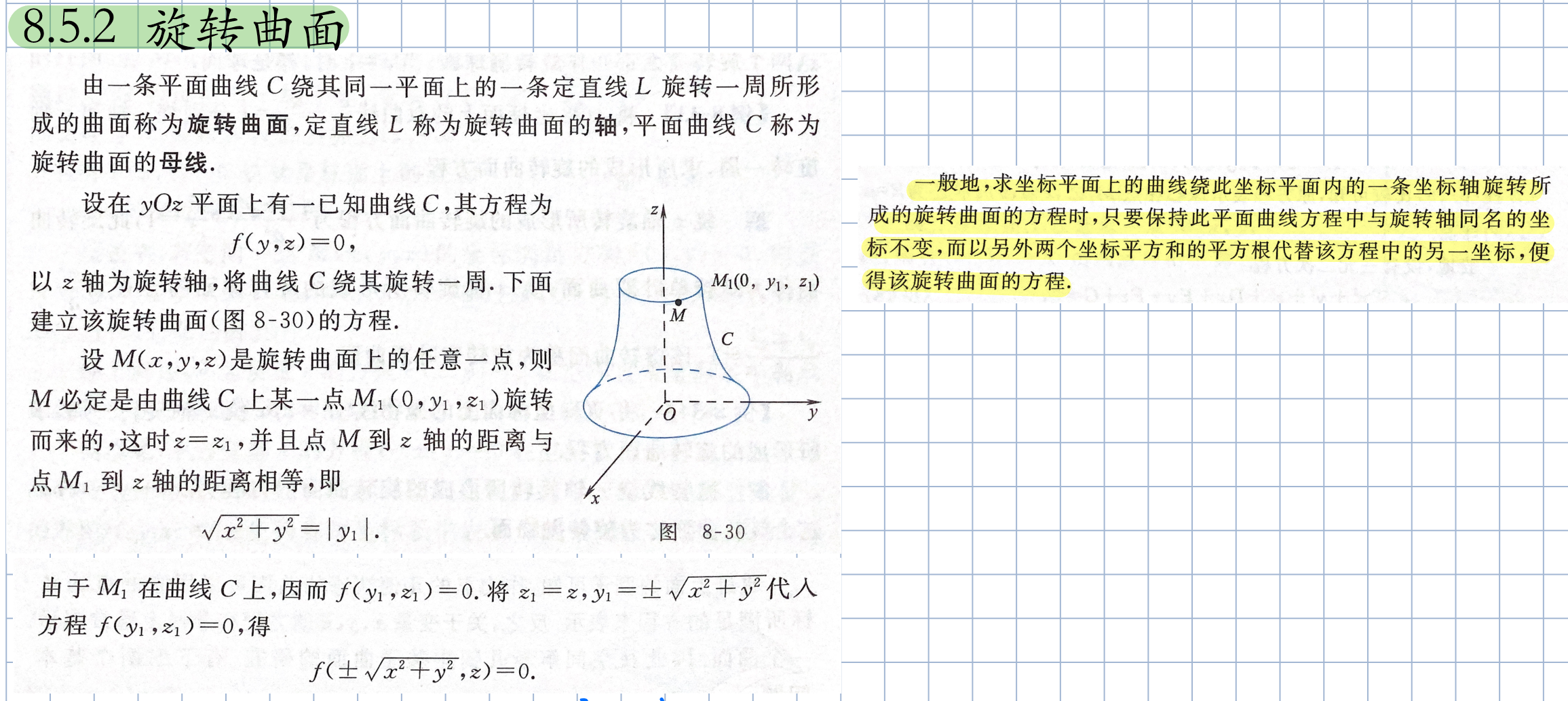
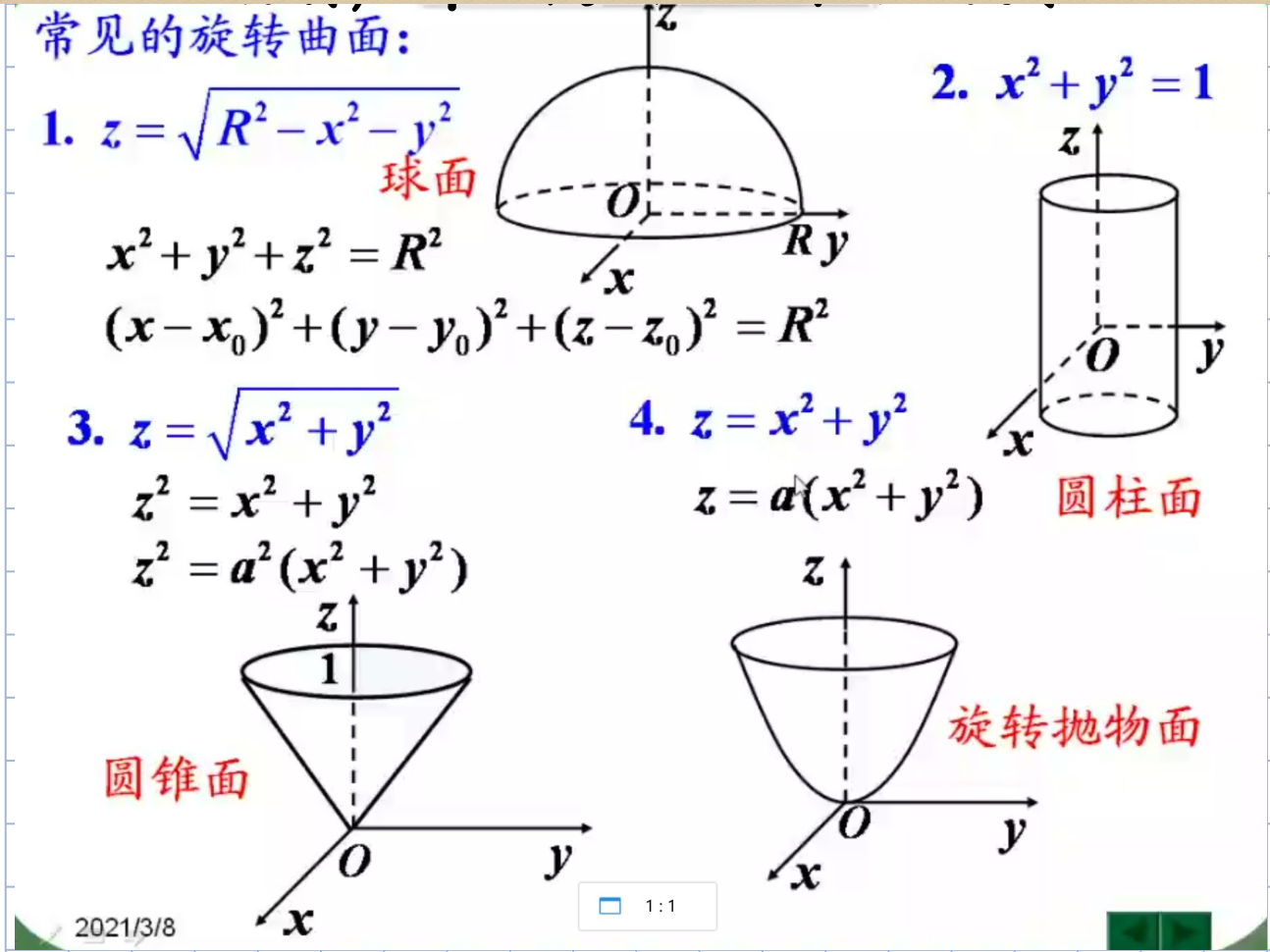
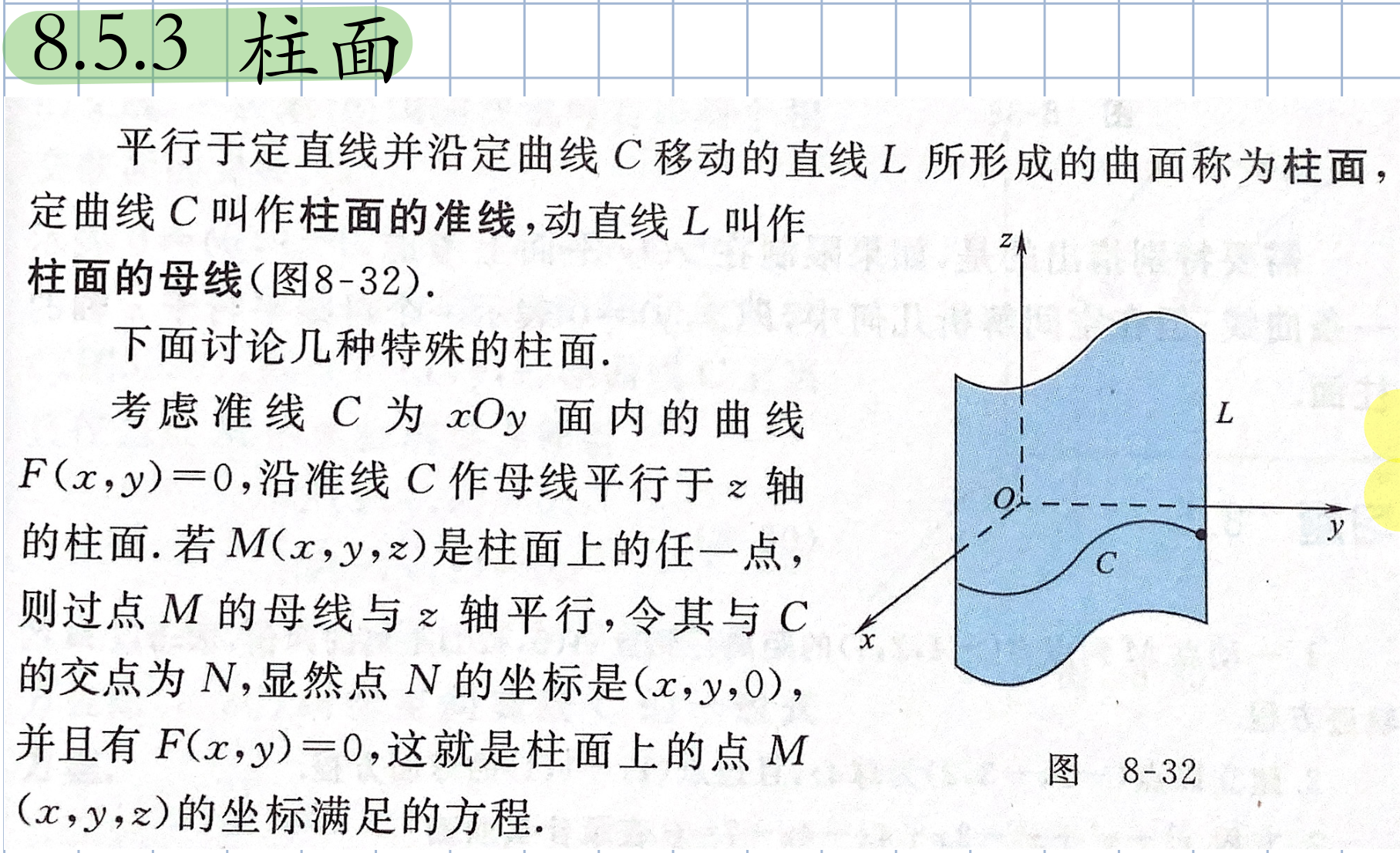
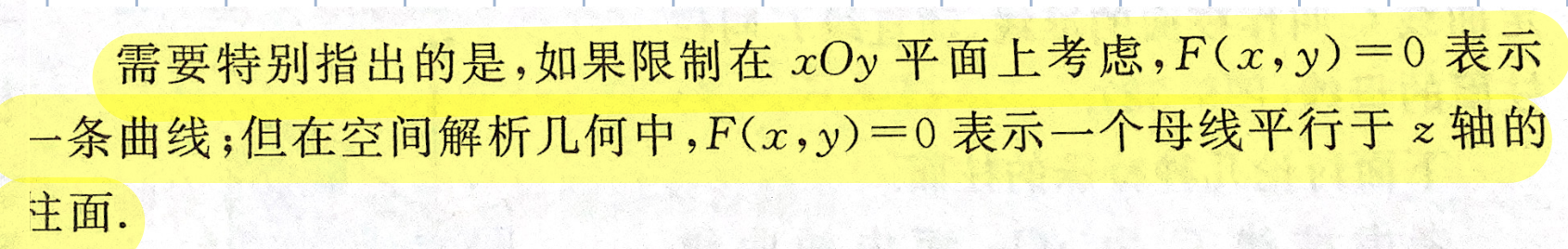
空间曲面及其方程
- 一般方程
- 参数方程
- 二次曲面

题型归纳
基本概念和判断
向量的运算与性质
向量的点乘运算
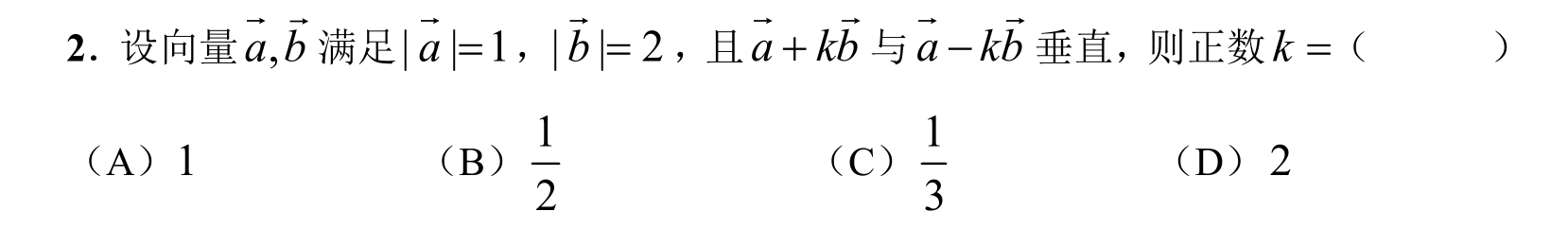
平面与直线的方程
求平面的方程
知识点
- 平面的方程的三种坐标表示(具体看前面知识点)
- 点法式:已知平面的法向量和平面上一点(常用)
- 平面上一条直线的方向向量垂直于平面的法向量(容易忘记该条件,在题目给出平面通过直线时要注意)
- 一般式:通过待定系数法,注意x,y,z前面的系数与平面法向量的关系
- 过原点的一般式表示
- 过x轴或y轴或z轴一般式的表示
- 平行x轴或平行y轴或平行z轴一般式的表示
- 截距式:知道平面与三个坐标轴的截距
- 点法式:已知平面的法向量和平面上一点(常用)
- 使用平面束求平面方程(涉及到直线方程)
题目1:点法式求平面方程


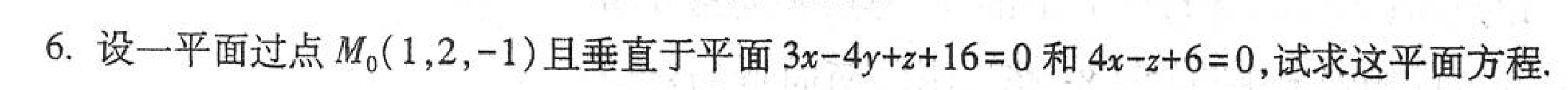

题目2:待定系数法求平面方程


题目3:平面束求平面方程


题目4:给出角度条件求平面方程


题目5:与直线相关的求平面方程
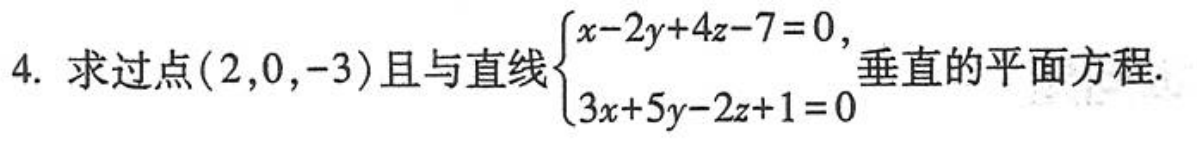



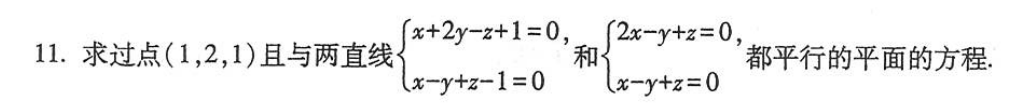


题目6:求切平面和法平面
-
这个内容与涉及到多元函数的几何意义
-
对于求曲线的法平面:都采用参数化法(与求切线和法线一样)
- 当曲线为均能用一个变量表示,那么就直接求导即可
- 当曲线为隐函数的时候,把x当做参数,分别求y关于x的导数,z关于x的导数,解方程得到两个导数
-
对于曲面的切平面:
- 当曲面均能用一个变量表示,那么就直接求导即可
- 直接将曲面方程当做关于x、y、z的多元函数,其x、y、z偏导的对应方程即为其对应法向量的坐标方程
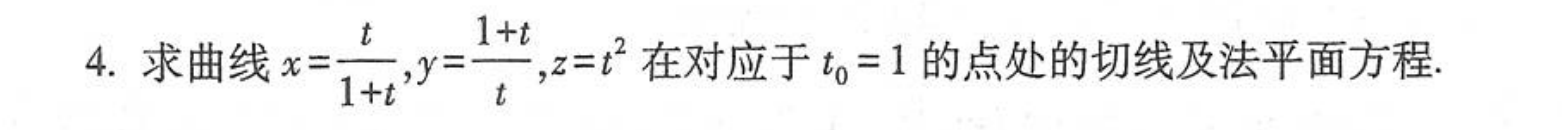
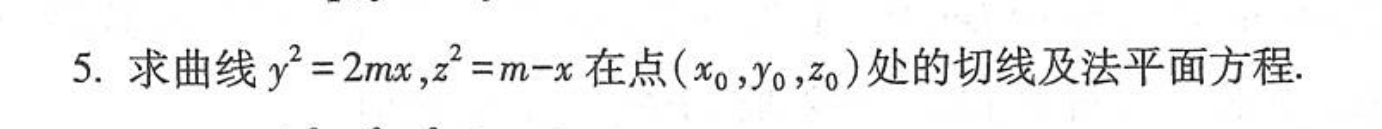
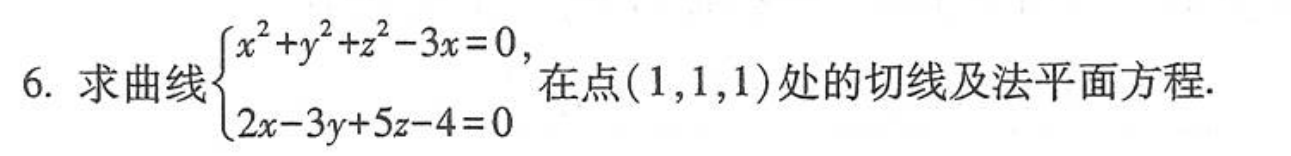

求空间直线的方程
知识点
-
利用点向式:直线上一点和直线方向向量
- 已知两个平面相交的交线为L,则这两个平面法向量的叉乘,是L的一个方向向量
-
利用一般式:两个平面相交所得交线
-
利用参数方程(不常用)
-
直线三个方程之间的相互转化
- 直线的一般方程转换为点向式方程:利用两个平面的法向量求直线的方向向量,再通过解方程确定直线上一点
- 点向式转换为参数方程,直接参考直线方程的内容
- 点向式转换为一般方程看下图



题目1:点向式求直线方程



题目2:与平面相关的求直线方程
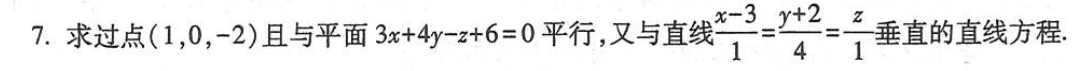

题目3:求切线和法线
- 对于求曲线的切线:都采用参数化法
- 当曲线为均能用一个变量表示,如下图问题1、2,那么就直接求导即可
- 当曲线为隐函数的时候,把x当做参数,分别求y关于x的导数,z关于x的导数,解方程得到两个导数
- 对于曲面的法线:都是参数化法
- 当曲面均能用一个变量表示,直接求导即可
- 直接将曲面方程当做关于x、y、z的多元函数,其x、y、z偏导的对应方程即为其对应法线方向向量的坐标方程



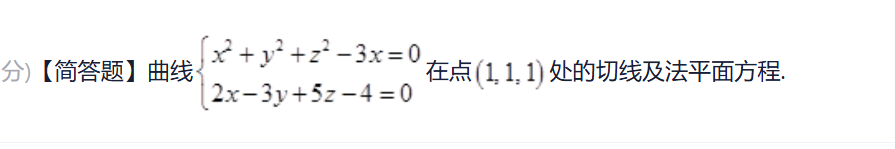
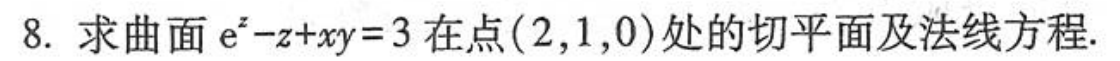
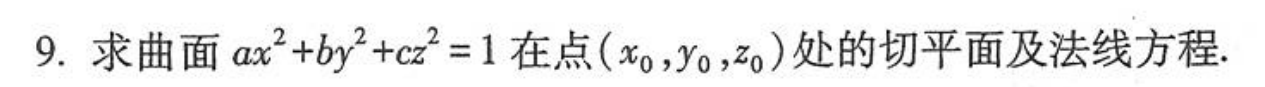
求直线与平面的交点
知识点
- 直线是点向式的情况:可以用参数方程求直线与平面的交点
- 直线是一般方程的情况:三个平面联立解方程得到交点
题目1:参数方程求交点

题目2:一般方程求交点
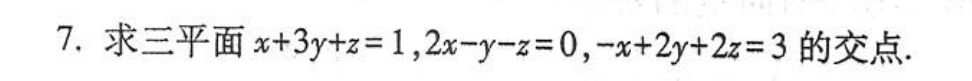

求投影问题
知识点
-
点到平面的投影:辅助直线法,利用平面法向量和点,得到过点且垂直于平面的一条直线,该直线与平面的交点就是点到平面上的投影
-
点到直线的投影:辅助垂面法,利用直线方向向量和点,得到过点且垂直于直线的一个平面,该平面与直线的交点就是点到直线上的投影
-
直线到平面的投影:
- 辅助平面法,利用直线的方向向量与平面的法向量叉乘得出辅助平面的法向量,再找一个交点得到辅助平面,辅助平面与平面相交即为投影线在面上的投影
- 辅助垂面法,利用平面束方程,求出过直线与平面垂直的平面,两平面的交线就是直线到平面上的投影
题目1:点到平面的投影


题目2:点到直线的投影
题目3:直线在平面上的投影直线


对称问题
- 对称问题在二维平面也属于是基础题
平面与直线的角
知识点
- 平面与平面的夹角:思路是求两个法向量之间的夹角余弦,公式如图
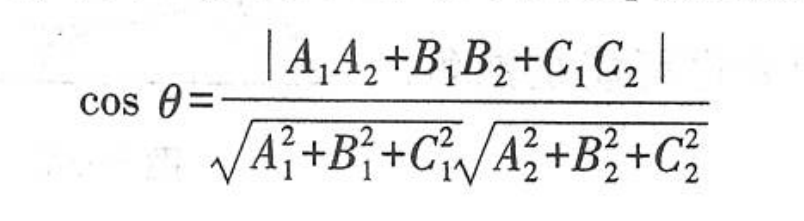
- 直线与直线的夹角:思路是求两个方向向量的夹角余弦,公式如图
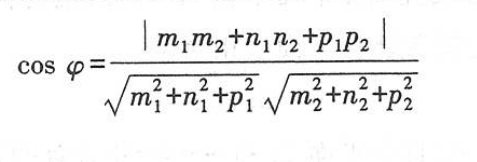
- 平面与直线的夹角:思路是求平面法向量和平面方向向量的夹角余弦,其值是平面与直线夹角的正弦

题目1:求平面与平面的夹角

题目2:求直线与直线的夹角


题目3:求直线与平面的夹角


平面与直线的距离
知识点
- 点到平面的距离:思路就是求向量在法向量上的投影,公式是二维点到直线的距离上升一个维度
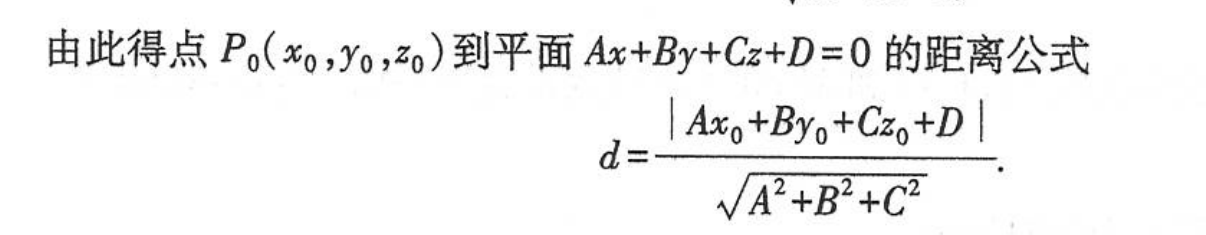
- 点到直线的距离:先求点在直线上的投影,再求两点距离即可。也可以套公式
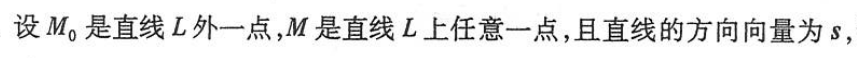
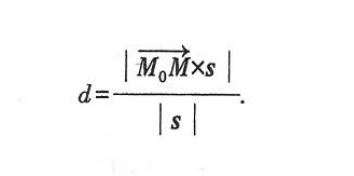
题目1:点到平面的距离
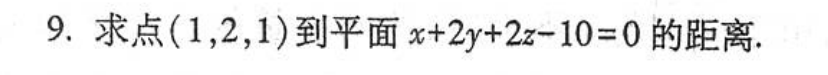

题目2:点到直线的距离


平移旋转问题
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 iyheart的博客!

