高数下第九章
- 注:知识点和例题来源于网络
多元函数微分发及其应用
多元函数的基本概念
多元函数的定义



多元函数的极限



多元函数的连续性


偏导数
偏导数及其计算法


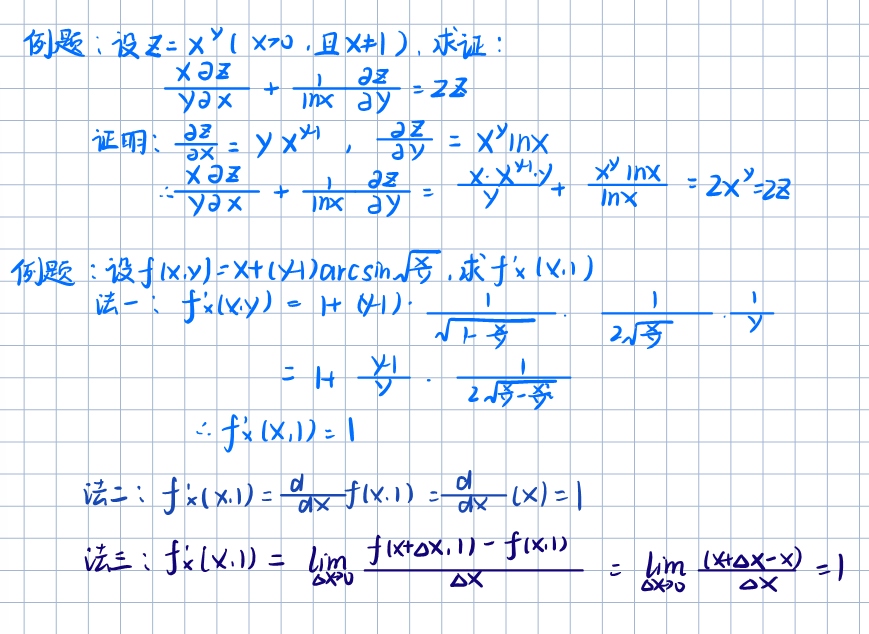


高价偏导数

全微分
全微分的定义

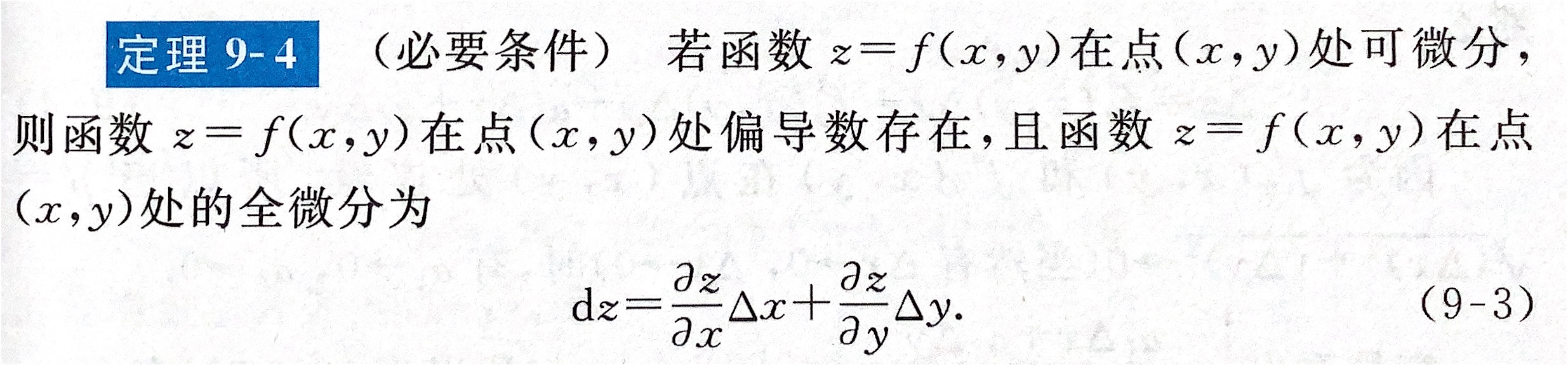

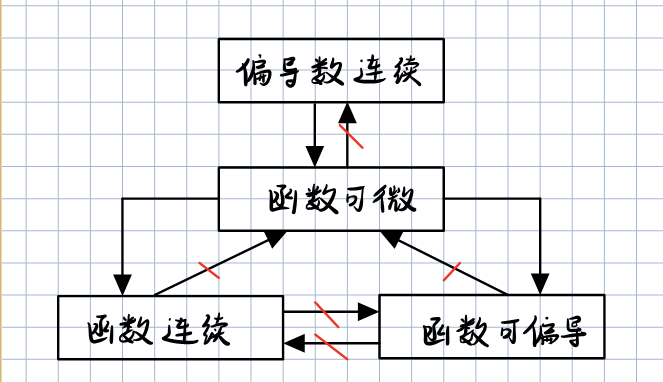


证明可微或不可微
-
证明可微:
- 从偏导数连续证明可微,判断二阶混合偏导是否相等,根据定理混合偏导相等即偏导数连续

- 利用可微的定义证明可微

- 证明不可微:
- 根据定义证明不可微分
- 偏导存在的逆否命题
- 原函数不连续
多元复合函数的求导法则
- 注意在多元复合函数求导的过程中先画图,找出中间变量和自变量
- 然后再记住单路相乘、异路相加、单路全导、叉路偏导(边做题边体会)
- 最后将所求得的式子的中间变量用自变量代换
例1:画出下面多元复合函数中自变量、中间变量、因变量的关系
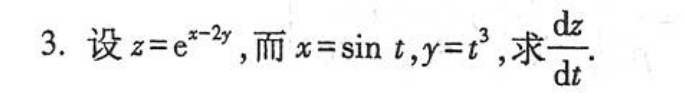

例2:画出下面多元复合函数中自变量、中间变量、因变量的关系
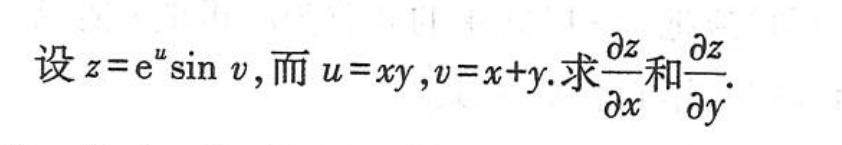
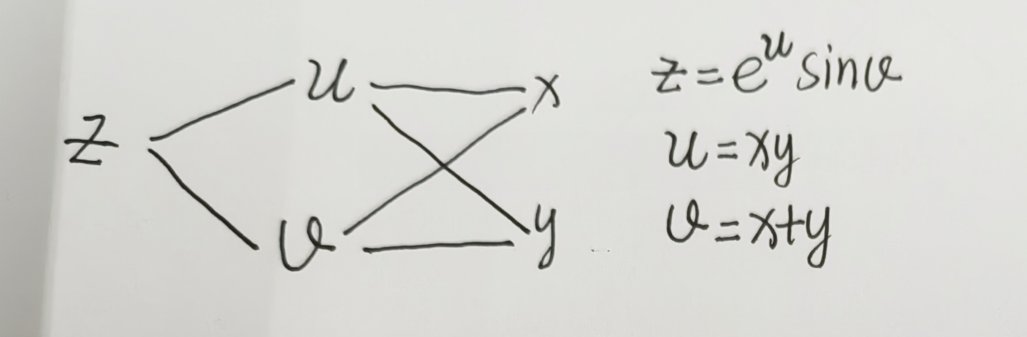
例3:画出下面抽象函数中因变量、中间变量、自变量的关系


一元函数与多元函数复合
知识点
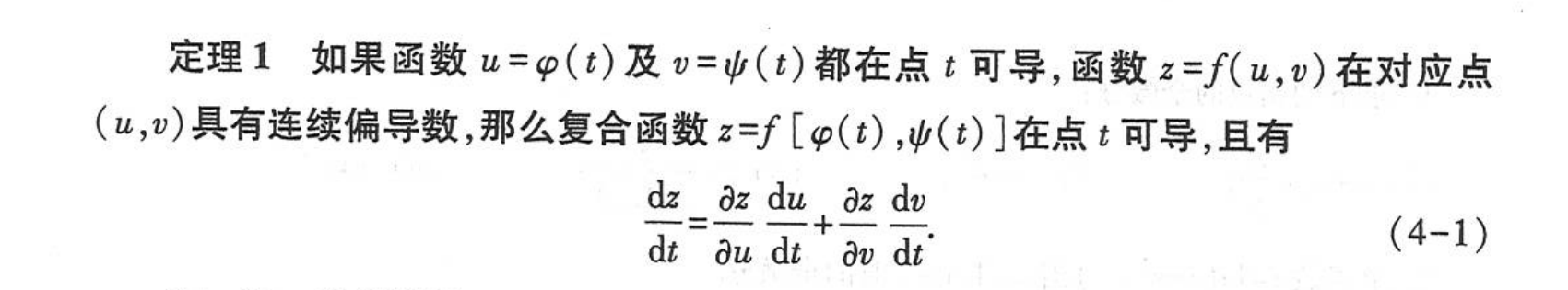
- 单路相乘,由上图z、x、t的关系可得一条从因变量到自变量的路线,通过因变量对中间变量的导数乘中间变量对自变量的导数即单路相乘
- 异路相加:由上图z、x、y、t的关系得,到自变量t由两条路,每条路都进行单路相乘后,再将两条路相加,即为异路相加
例题
例题1
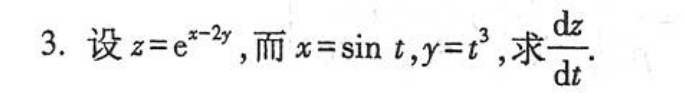
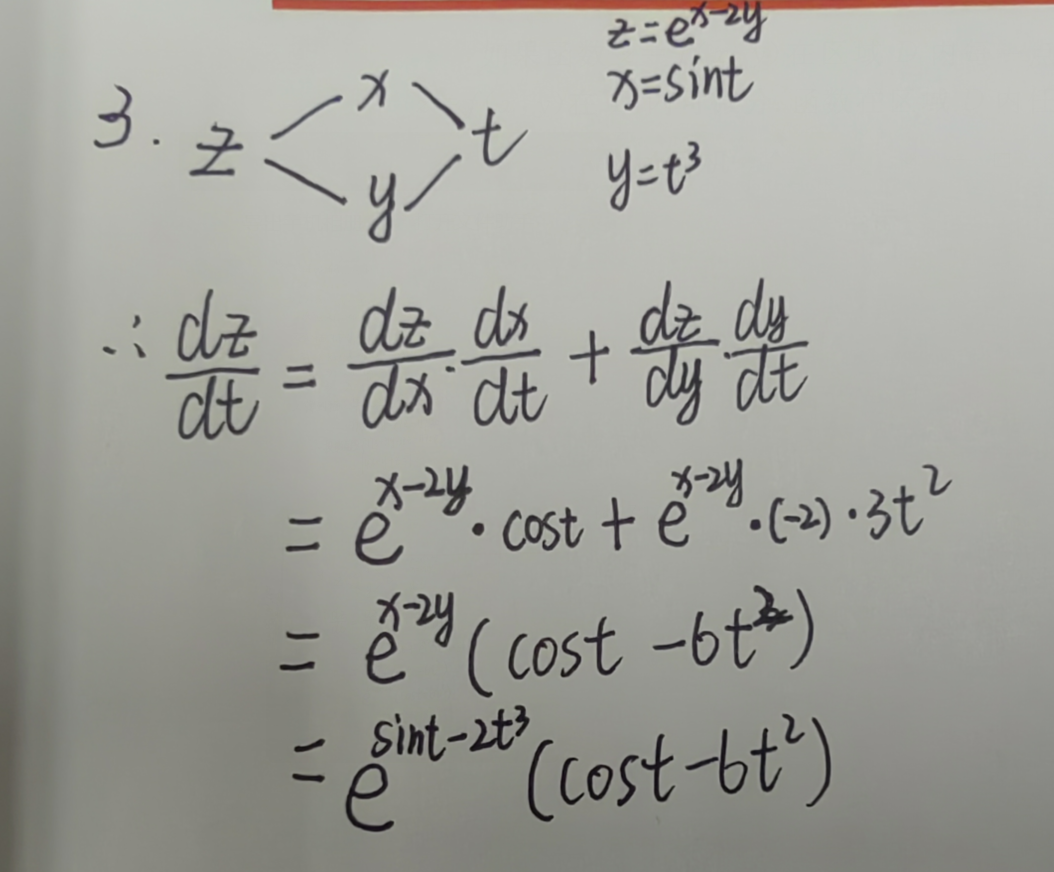
例题2
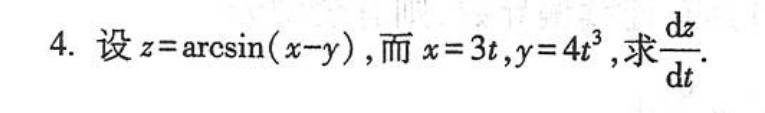
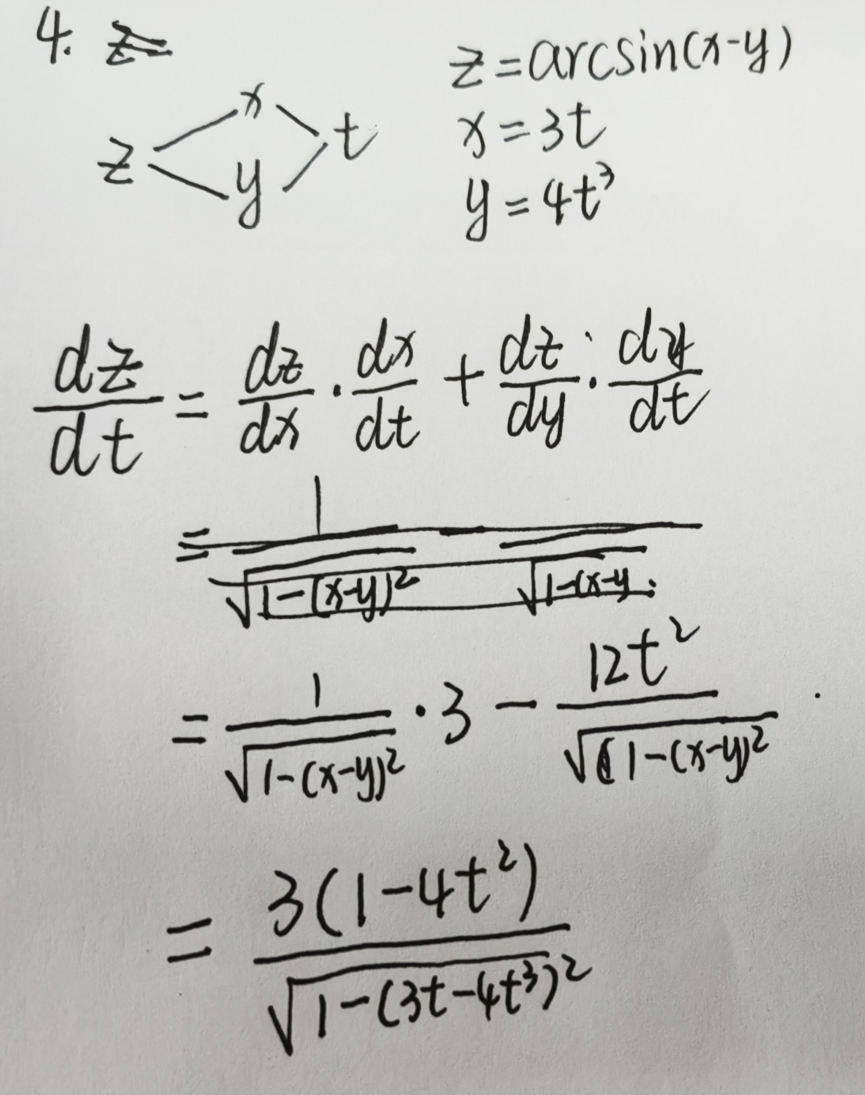
多元函数与多元函数复合
知识点


- 单路全导:如果在中间变量和自变量之间(因变量与中间变量之间)没有叉路,那么就是求自变量的全导数
- 叉路偏导:如果在中间变量和自变量之间有叉路(如下图例1所示u与x、y有叉路),那么就求偏导,走自变量x那条路就对x求偏导,走自变量y那条路就对y求偏导
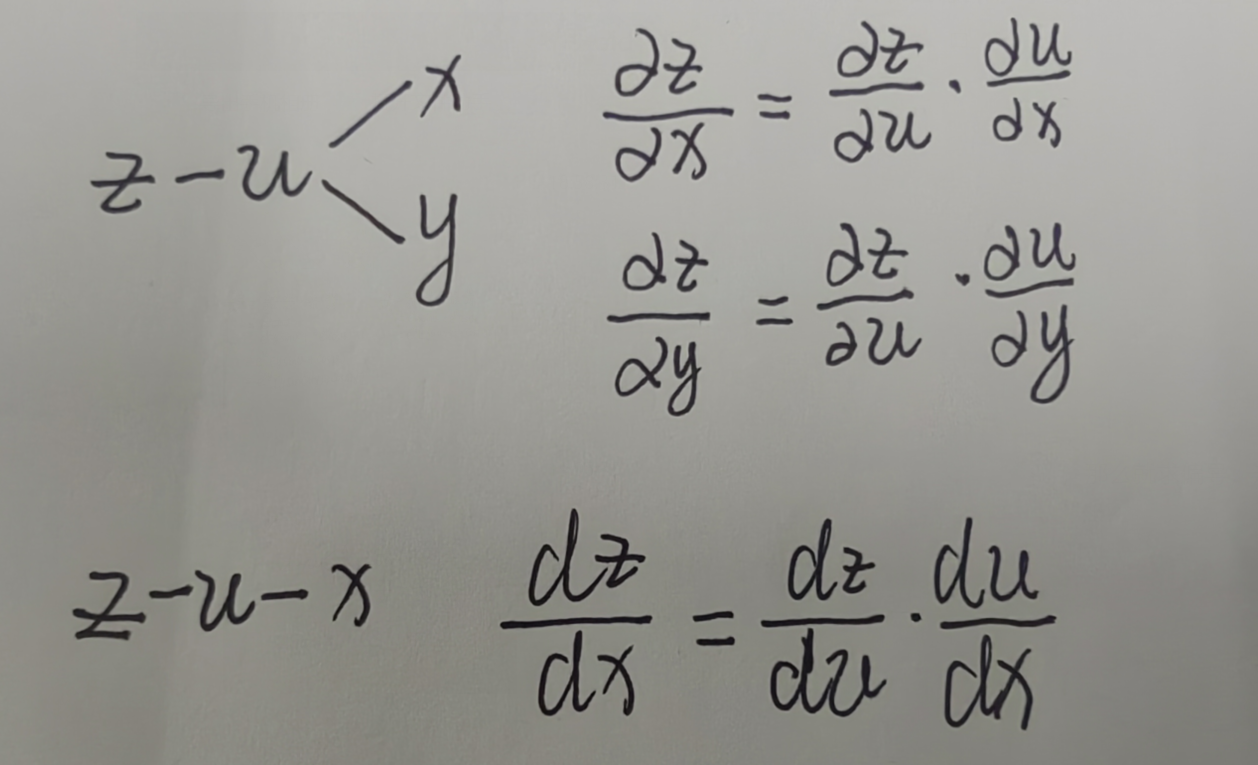
例题
例题1:
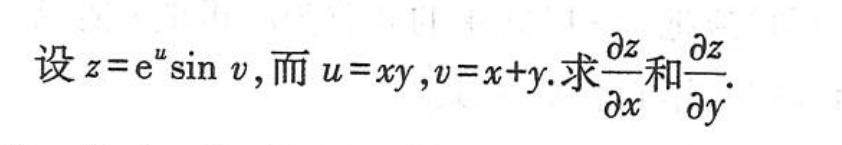
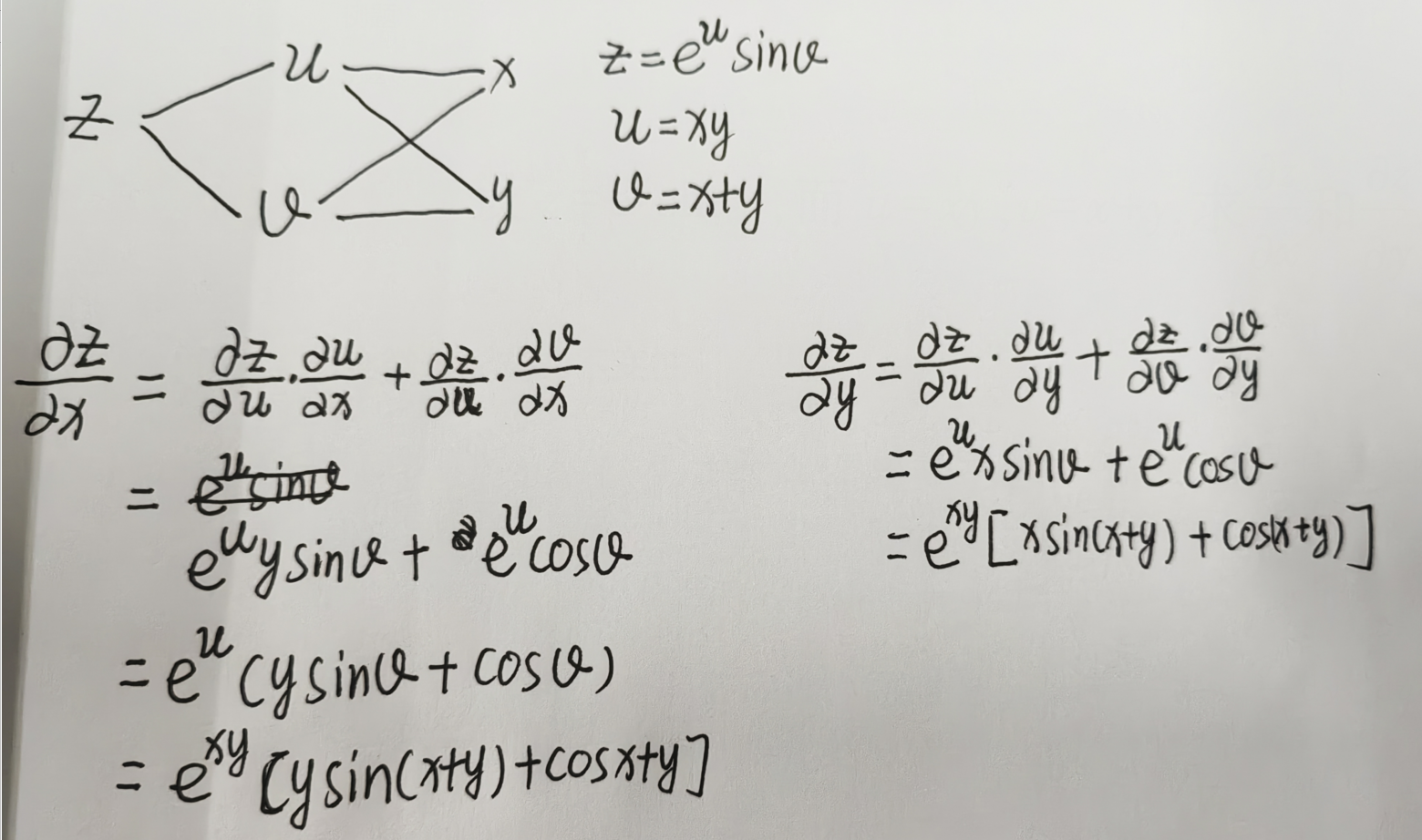
例题2:

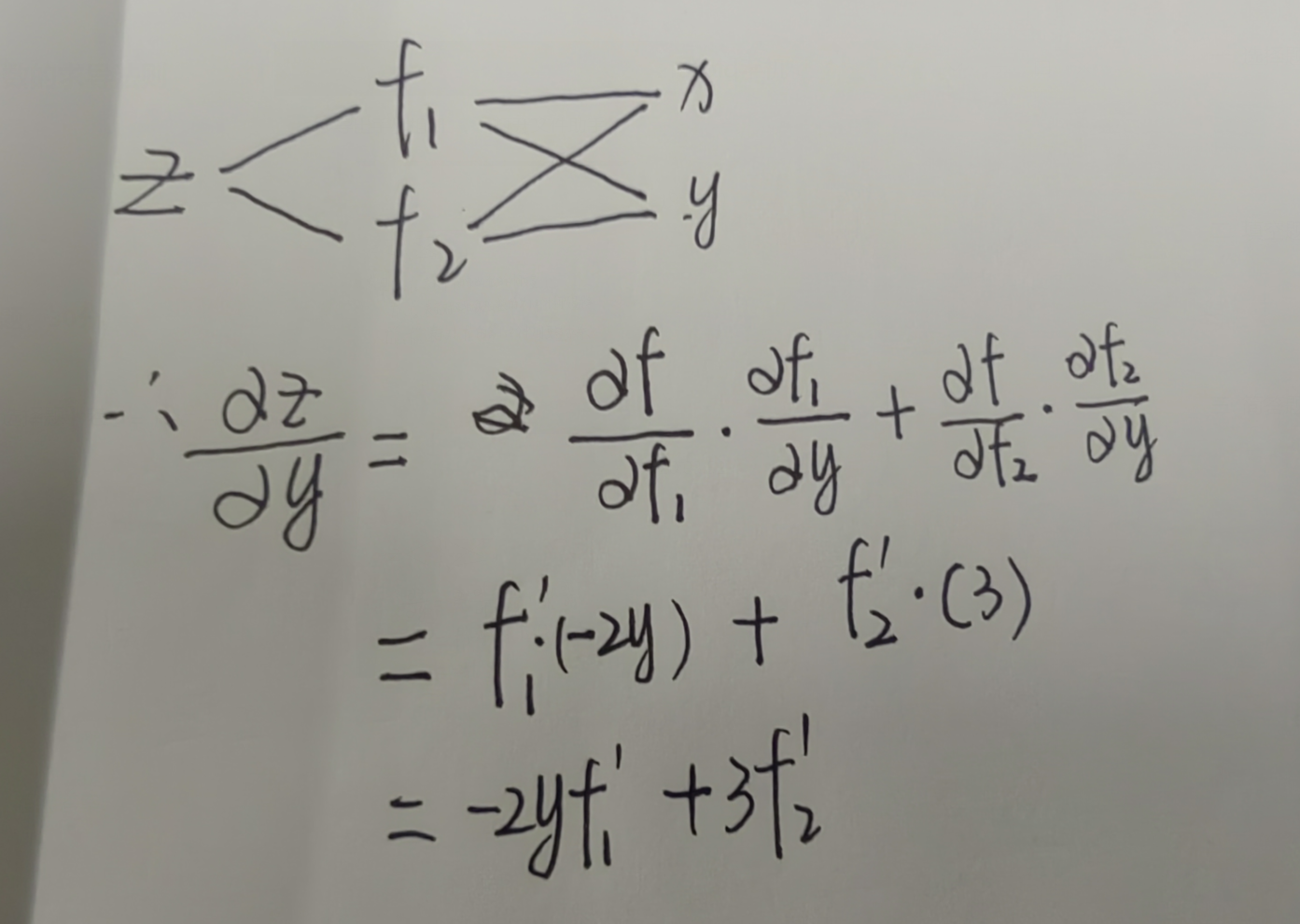
例题3:
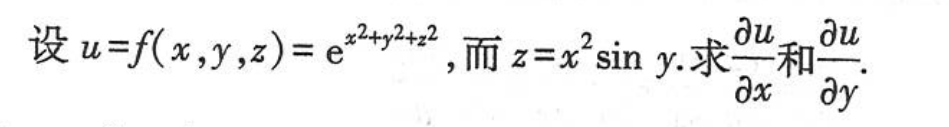

例题4:
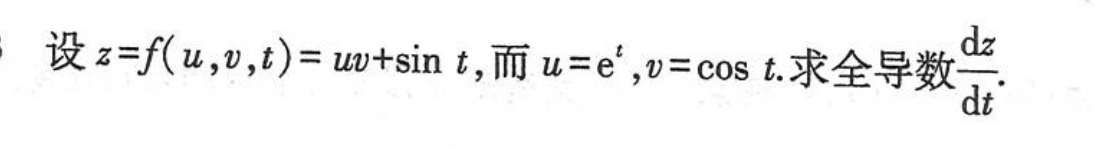
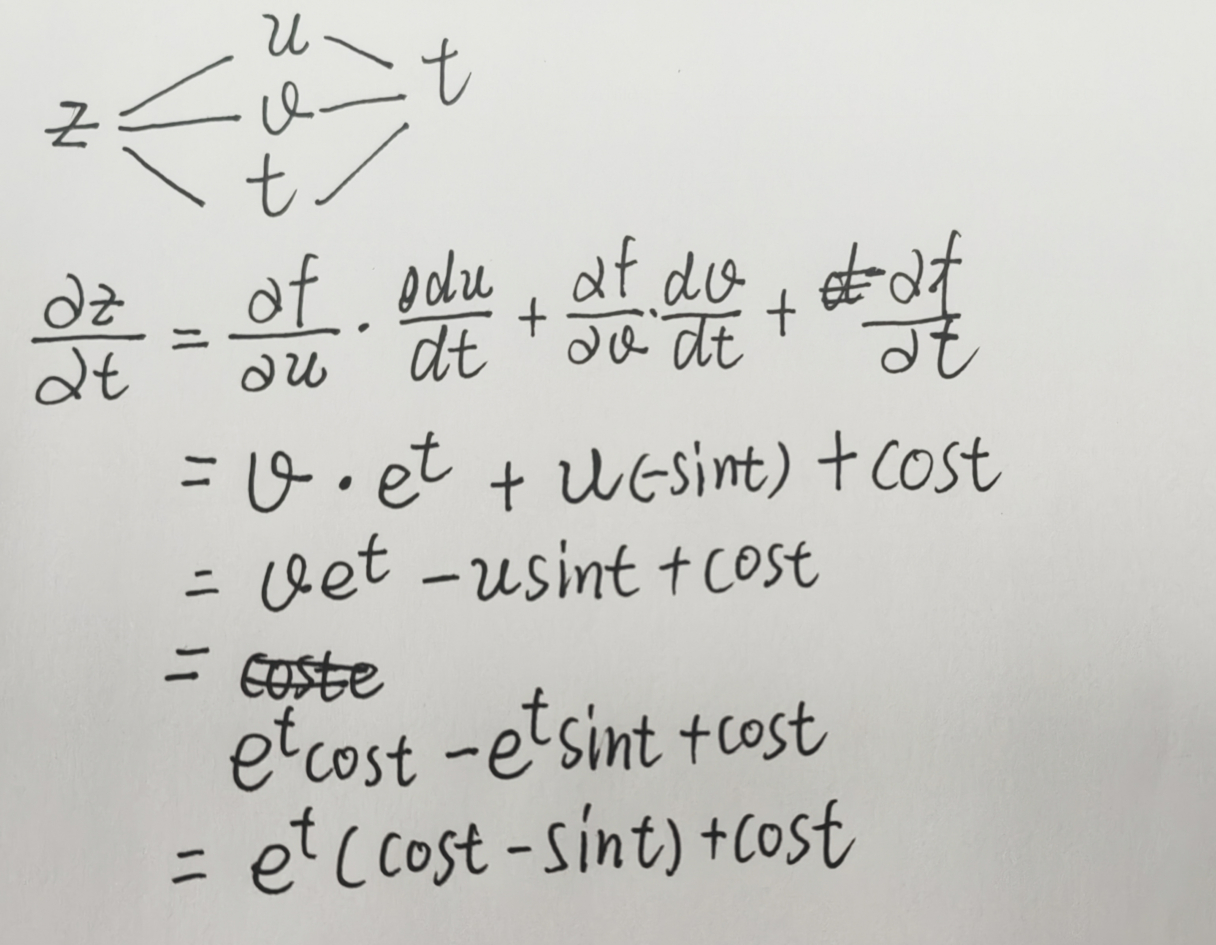
全微分形式的不变性


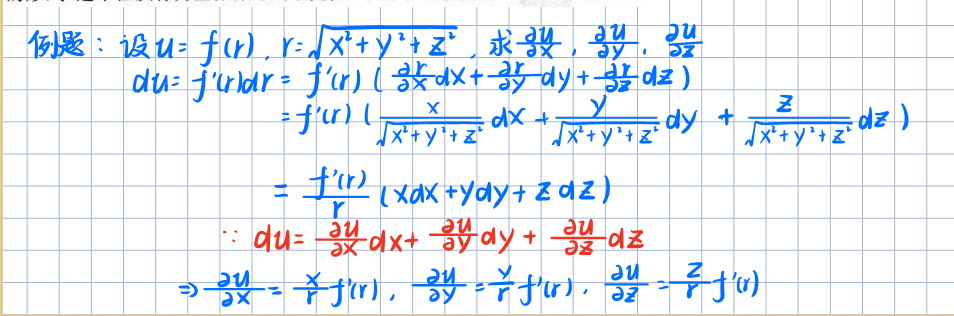
隐函数的求导公式






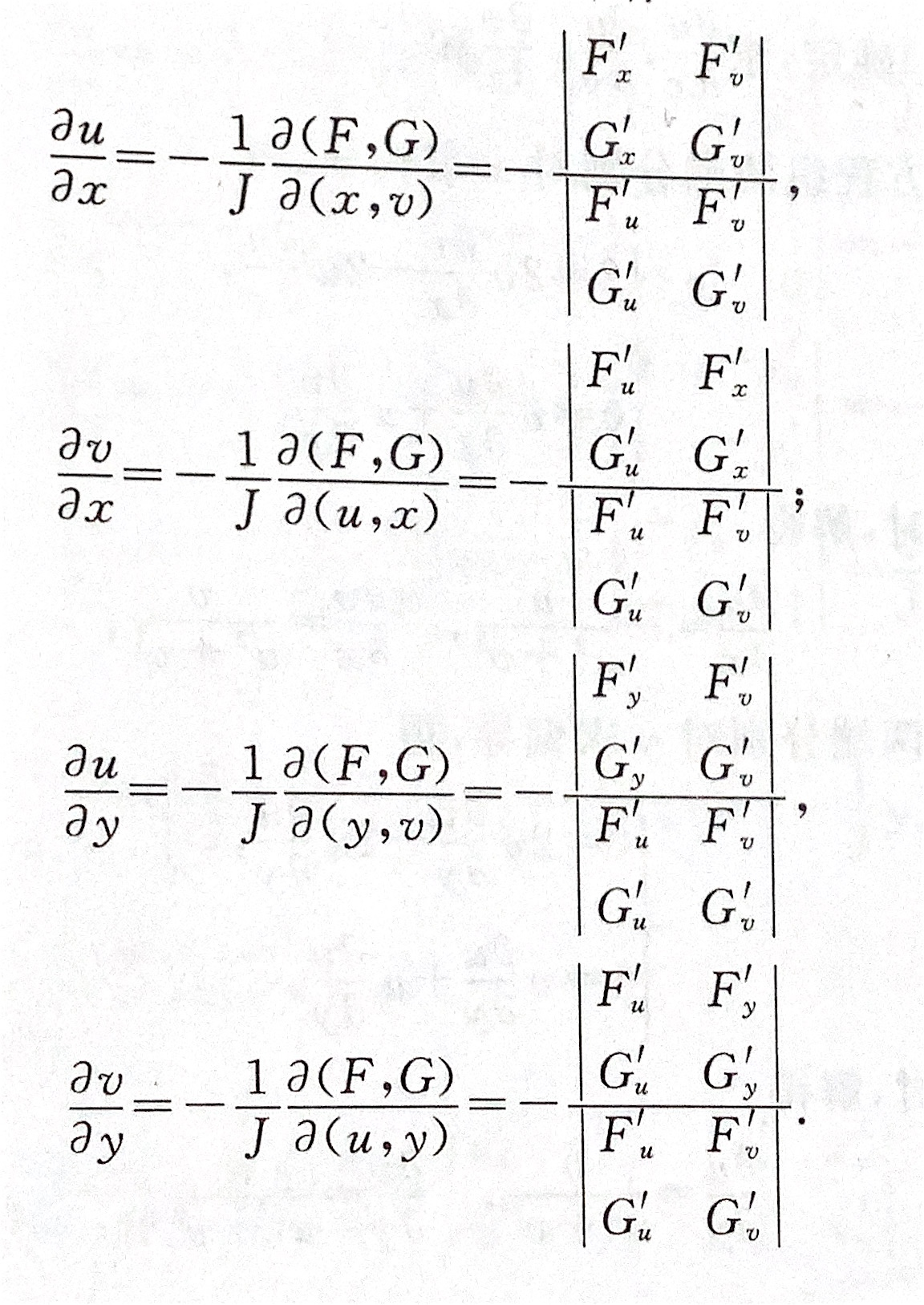

多元函数微分学的几何运用
空间曲线的切线与法平面
- 曲线方程为参数方程的情况
- 曲线方程为一般式的情况


曲面的切平面与法线

- 注:例题第一题中法线方程求错了
方向导数与梯度
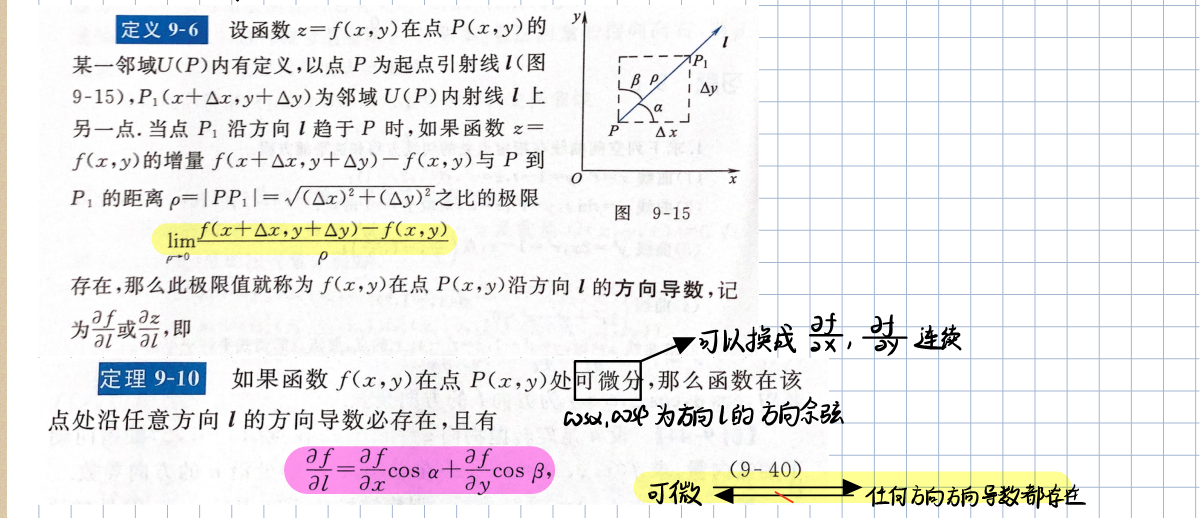




多元函数的极值及其求法
- 多元函数的极值




- 条件极值 拉格朗日乘数法





题型归纳
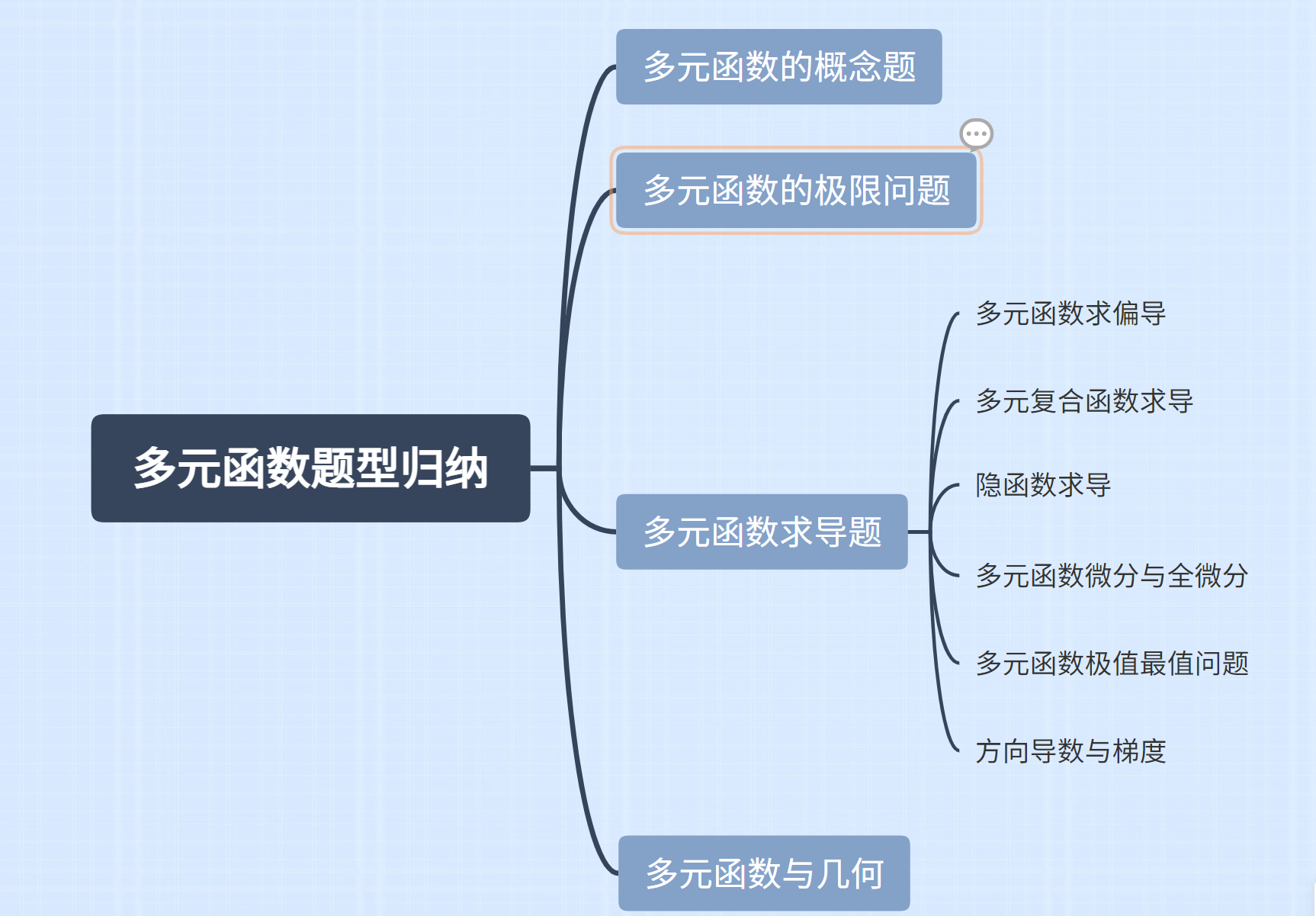
多元函数的概念
知识点:
- 知道多元函数连续、多元函数可偏导、多元函数可微、多元函数偏导数连续之间的充分必要关系

相关概念和关系的判断


判断是否连续
判断是否可偏导
判断可微
多元函数的极限问题
多元函数微分与全微分
多元函数求导问题
多元函数求偏导
多元复合函数求导
- 一元函数与多元函数复合:外层函数是多元函数,内层函数是一元函数
- 多元函数与多元函数复合:外层和内层函数均是多元函数
- 多元抽象复合函数的求导:抽象的多元函数复合
- 多元复合函数求二阶导(求一阶导的问题归类到前面3个问题中)
隐函数求导
- 公式法对隐函数求导(只适合隐函数求一阶导)
- 求导法对隐函数求导
- 方程组形式的隐函数求导
多元函数极值最值问题
知识点:
-
多元函数极值点的判别
-
求多元函数的极值
- 步骤1:
- 步骤2:
- 步骤3:
-
拉格朗日数乘法求多元函数的条件极值
方向导数与梯度(小题)
知识点:
- 方向导数是一个数
- 梯度是一个向量
多元函数与几何问题
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 iyheart的博客!
评论

