RC4加密

RC4加密现在虽然有在线网站可以一键解密，但是碰到一些变式就GG了，所以还是要学习一下具体的加密过程
RC4加密有几个特点：
- 是典型的对称加密，即加密和解密使用的是同一套算法，即知道密钥和密文就可以通过算法得到明文。
- RC4是流密码，一个字节一个字节的进行加密，与块加密区分开来
- 密钥长度可变，它以一个足够大的表S为基础，对表进行非线性变换，产生密钥流

加密过程

加密过程大致也就两步，初始化S表和密钥流的生成

初始化S表

对S表进行线性填充，一般为256个字节
用种子密钥填充另一个256字节的K表
- 如果种子密钥刚好等于256字节，那么就直接赋值给k表
- 如果种子密钥小于256字节，就循环赋值给k表，直到k表的256字节都被填充
用k表对S表进行初始置换，即通过算法将s表中的各个元素相互交换。下面给出一个例子：

密钥流生成

为每个待加密的字节生成一个伪随机数，用来异或。注：表S一旦完成初始化，种子密钥就不再被使用

maze问题

简介

maze问题，即迷宫问题，是ctf基础经典题目，基础题偏向娱乐，有难度的题就涉及到回溯算法了。
maz问题有以下特点
- 在内存中会布置一张“地图”，静态地图可能是在程序中的一些段中，而动态的地图会在内存中可能随机生成
- 将用户输入限制在少数范围内，比如“W”、“S”、“A”、“D”,表示前后左右，走迷宫，也可能会更多
- 一般只有一个迷宫路口和一个迷宫出口
地图：布置的地图可以由可显字符如“#”和"*"组合而成，通过查看字符串基本就知道是迷宫题目了，有时候地图是在运行的时候才加载到内存中，这个时候就需要使用动态调试的方法，将该地图提取出来
迷宫的特点：
- 一般情况下迷宫只有1个入口和1个出口，入口的位置一般在最左上角（0,0）位置，而出口在最右下角（max_X,max_Y）处，
- 有时候迷宫的出口也可能在正中心
- 出口一般用字符Y表示

方法

maze问题在逆向的过程中都会出现很多if语句、数组的大小和长度
通过if语句我们就可以判断什么地方是墙、什么地方是死路、什么地方才是正确的路径，还能确定终点和起点，还有一些字符对应的方向
而通过数组的我们可以了解到这个迷宫是几行几列的迷宫，进而更直观的看到迷宫的整体布局。
寻找顺序为：先找到迷宫，再找到限制字符，分析路径（在分析路径之前先确定迷宫是几行几列的），得出路径。（了解了方法就可以做level_1）的题目了

基础题目

题目1–level_1_maze

来源：2024baseCTF新生赛：基地：：CTF (basectf.fun)，（之后平台会关闭，可以到该平台复现https://gz.imxbt.cn/）
题目附件：https://wwsq.lanzoue.com/ia6fG29wjr8d 密码:h8bp
拿到附件直接使用IDA反编译看到main函数

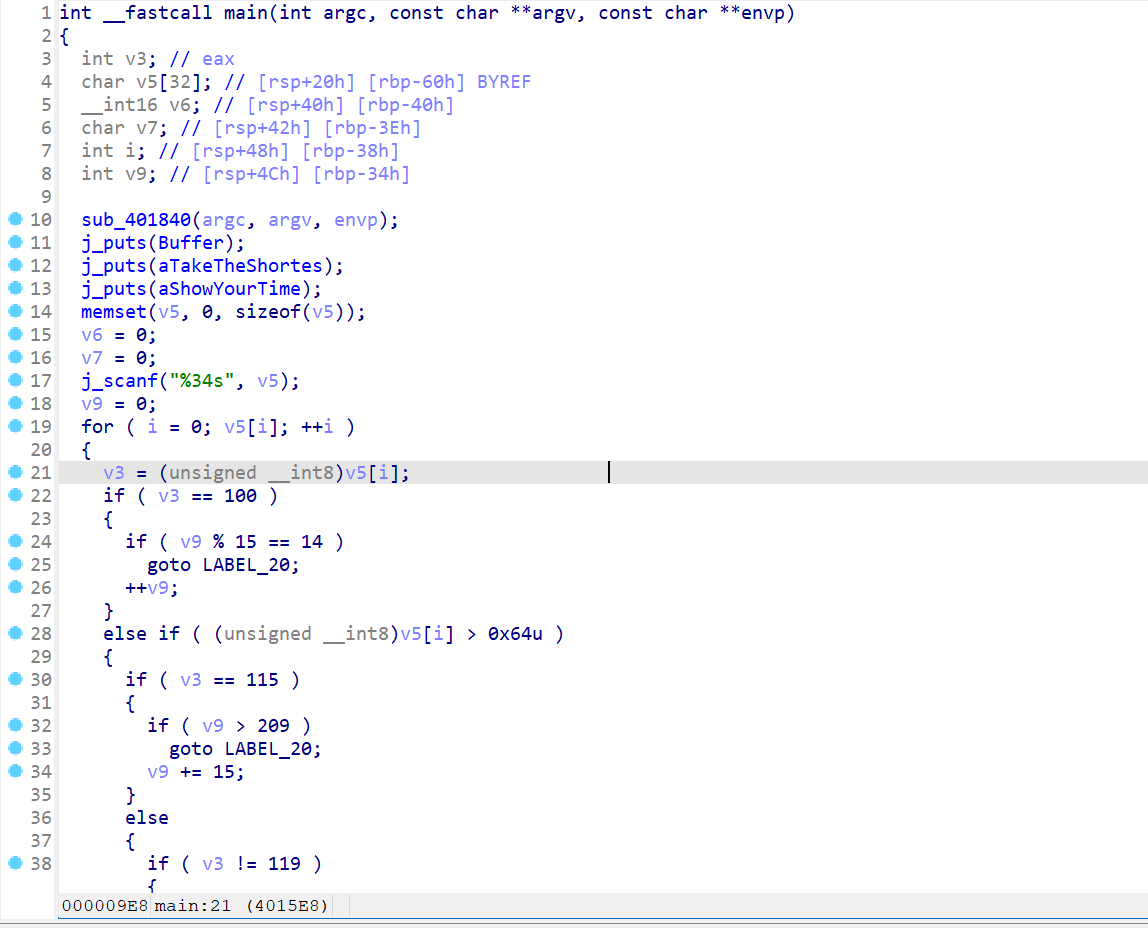
分析1

先使用shift + F12 按键查看一下程序中的字符串，发现字符串中给出了俩个关键信息
- 其中一个就是迷宫
- 而另一个是flag的格式

这时候我们就找到了迷宫，迷宫找到之后双击点击该迷宫的字符串，跳转到相应位置，将迷宫的这个字符串复制下来，先放到记事本里面，这样第一步找到迷宫就完成了

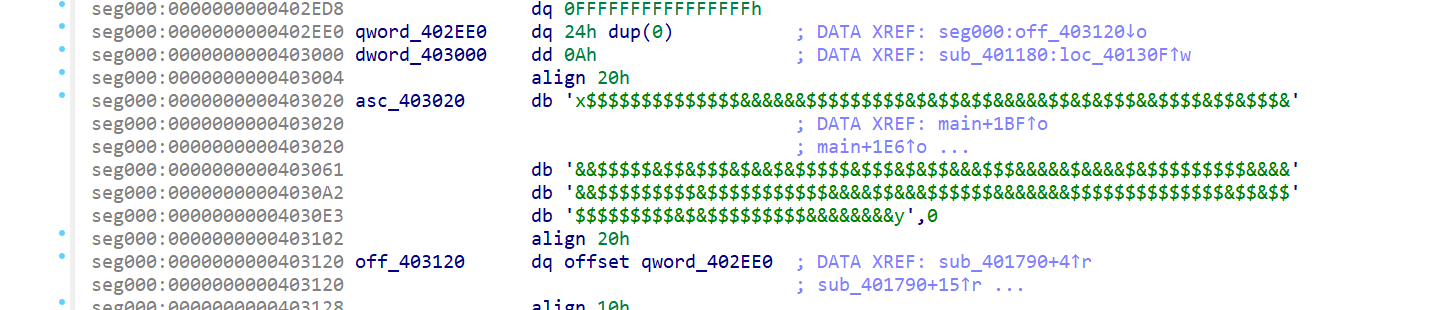
分析2

认真读懂代码，并将if判断等号右边的数字，使用快捷键R将其转化成字符
经过逆向分析发现限制的字符是a、d、w、s

然后又确定了$字符是墙，y字符是出口

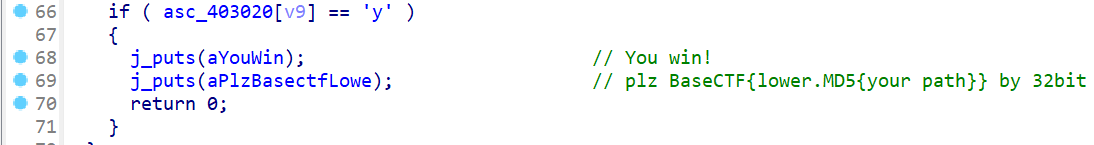
分析3

现在开始分析路径，在分析路径前，我们先要知道这个迷宫有几行几列，如何找，看awsd这几个if的判断后的操作，和一些相关的数组，从d这里可以判断d是向右走1格，而如果v9%15 = 14，就会提示出现边界，这就表明该迷宫有15列

if ( v3 == 'd' )
    {
      if ( v9 % 15 == 14 )
        goto LABEL_20;
      ++v9;
    }

LABEL_20:
        j_puts(aInvalidMoveOut);                // Invalid move: out of bounds!
        return -1;
      }

这里再对s进行分析,发现s是向下走一格

if ( v3 == 's' )
{
    if ( v9 > 209 )
      goto LABEL_20;
    v9 += 15;
}

接着分析a、w，得到a是向左一格w是向上一格
所以得到迷宫的列数为15，即一行有15个元素，这时我们再根据得到的迷宫字符串按照一行15个字符串就可以得到迷宫的分布图像了
为了方便我这里使用Python进行输出迷宫布局，得到如图所示的迷宫图

a = 'x$$$$$$$$$$$$$$&&&&&&$$$$$$$$$&$&$$&$$&&&&&$$&$&$$$&&$$$$&$$&$$$&&&$$$$$&$$&$$$&$&&$&$$$$$&$$$&$&$$&&&$$$&&&&&$&&&&$&$$$$$$$$$&&&&&&$$$$$$$$$&$$$$$$$$$$$&&&&$$&&&$$$$$$&&&&&&&$$$$$$$$$$$$$$&$$&$$$$$$$$$$$&$&$$$$$$$$$&&&&&&&&y'
print(len(a)//15) # 15
for i in range(15):
    print(a[0+i*15:15+i*15])

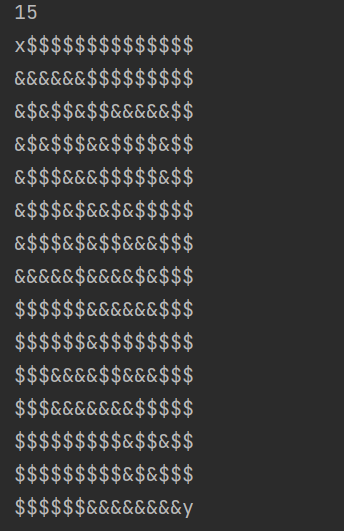
最后就是简单的走迷宫了，这题是比较基础，没有涉及到回溯算法，直接看图走即可，不用编写脚本，这里直接附上路径和flag

1 2	路径：sssssssddddwwwddsssssssdddsssddddd flag：BaseCTF{131b7d6e60e8a34cb01801ae8de07efe}

题目2–level_2_maze

本题的迷宫题目迷宫并没有直接放在程序段中，而是在程序运行的时候加载到内存中。所以本题需要进行动态调试。在做本题之前，先要学会IDA的动态调试。
题目来源：

进阶题目

题目3–level_3_maze

本题的迷宫题的进阶问题，并不是偏向娱乐的迷宫题目了，该题的迷宫是寻找最优路径，所以在此之前需要先完成level_2（因为有用上动态调试），还要学会编写深度优先搜索算法和广度优先搜索算法这样才会能编写脚本来算出最优路径

Z3约束求解器

参考来源：星盟安全Re系列教程

介绍

Z3约束求解器，全称为Z3 - Solver
- 是一个用于求解数学和逻辑问题的高性能库函数。它是由微软研究院开发的，提供了一个功能强大的求解器，可以解决各种形式的数学和逻辑约束问题
- Z3支持多种不同的问题领域，包括布尔逻辑、整数和实数的线性和非线性算术、位向量、数组、集合、函数等。它的主要应用领域包括软件验证、形式化验证、程序分析、人工智能和自动定理证明。
- 简单来说方便解方程，当一个方程有好几组解，可能只会输出一个解，在添加约束条件时，条件需要添加足够，需要添加多一点。

安装

Z3安装最简单直接使用pip install z3-solver

使用

创建声明

x = Int('x') 		#声明整数
x , y = Ints('x y') #批量声明，复数形式就行
x = Real('x') 		#声明实数
x = Bool('x')   	#声明布尔类型
x = BitVec('x',8)   #声明向量类型
a , b, c = Reals('a b c')  # 批量声明

常用API

1. 创建约束求解器
	solver = Solver()
2. 添加约束条件
	solver.add()
3. 判断解是否存在，在求解之前必须调用这个，否则报错
	solver.check()
4. 求解
	print(solver.model())

例：

# 求符合条件的整数x,y
# 其中 x > 2,y < 10 , x + 2*y == 7
# 尝试解题，看着上面的创建声明和调用API试着解决，不要看下面的代码
from z3 import *
x,y = Ints('x y')
solver = Solver()
solver.add(x > 2)
solver.add(y < 10)
solver.add(x+2*y==7)
solver.check()
print(solver.model())

题目

题目1–level_1_z3

本人建议不要做这题，跳到level2（此题以废但是不想删除写了这么久的文章，牢题目。约束条件太少能很快跑出来，但是得不到想要结果，约束条件稍微多一点跑不动（也可能是条件还不够多），当条件满足31个方程的时候，就直接sage解方程就行了），总之是不想再写一遍了。
本题其实是个misc题目，以此题来帮助练习z3的使用
题目来源：中国海洋大学的校赛题目
题目附件（如有侵权请在评论区留言，本人看到立马删除）：https://wwsq.lanzoue.com/i95Cy29x9ffe 密码:5m3d
当时做的挺牢的，“动帧格题目”，一张一张拍照，然后转文本，提取一闪而过的含有30几个未知数的个方程。
使用这个加载视频:https://app.clipchamp.com/ 然后逐帧找到，跳转出来的图片

将图片中的方程转换为文本，可以用图片识别工具或者AI进行

76*a1 + 23*a2 + 47*a3 + 95*a4 + 56*a5 + 94*a6 + 9*a7 + 89*a8 + 
1*a9 + 27*a10 + 64*a11 + 54*a12 + 77*a13 + 57*a14 + 11*a15 + 
80*a16 + 61*a17 + 98*a18 + 14*a19 + 72*a20 + 67*a21 + 98*a22 + 
66*a23 + 26*a24 + 11*a25 + 36*a26 + 94*a27 + 66*a28 + 99*a29 + 
64*a30 + 40*a31 = 171444

然后使用Python，先输出31个未知数

for i in range(1,32):
    print('a' + str(i),end=' ')
print('')
for i in  range(1,32):
    print('a' +str(i)+ ',',end=' ')
print()
for i in range(1,32):
    print('a' + str(i) + '<255' + ',',end=' ')

输出结果如下

a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20 a21 a22 a23 a24 a25 a26 a27 a28 a29 a30 a31

a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15, a16, a17, a18, a19, a20, a21, a22, a23, a24, a25, a26, a27, a28, a29, a30, a31

a1>255, a2>255, a3>255, a4>255, a5>255, a6>255, a7>255, a8>255, a9>255, a10>255, a11>255, a12>255, a13>255, a14>255, a15>255, a16>255, a17>255, a18>255, a19>255, a20>255, a21>255, a22>255, a23>255, a24>255, a25>255, a26>255, a27>255, a28>255, a29>255, a30>255, a31>255,

这里附上未完成的代码

for i in range(1,32):
    print('a' + str(i),end=' ')
print('')
for i in  range(1,32):
    print('a' +str(i)+ ',',end=' ')
print()
for i in range(1,32):
    print('a' + str(i) + '<128' + ',',end=' ')

from z3 import *
a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15, a16, a17, a18, a19, a20, a21, a22, a23, a24, a25, a26, a27, a28, a29, a30, a31 = Ints('a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20 a21 a22 a23 a24 a25 a26 a27 a28 a29 a30 a31')
solver = Solver()
solver.add(76*a1 + 23*a2 + 47*a3 + 95*a4 + 56*a5 + 94*a6 + 9*a7 + 89*a8 + 1*a9 + 27*a10 + 64*a11 + 54*a12 + 77*a13 + 57*a14 + 11*a15 + 80*a16 + 61*a17 + 98*a18 + 14*a19 + 72*a20 + 67*a21 + 98*a22 + 66*a23 + 26*a24 + 11*a25 + 36*a26 + 94*a27 + 66*a28 + 99*a29 + 64*a30 + 40*a31 == 171444)
solver.add(a1<128, a2<128, a3<128, a4<128, a5<128, a6<128, a7<128, a8<128, a9<128, a10<128, a11<128, a12<128, a13<128, a14<128, a15<128, a16<128, a17<128, a18<128, a19<128, a20<128, a21<128, a22<128, a23<128, a24<128, a25<128, a26<128, a27<128, a28<128, a29<128, a30<128, a31<128)
solver.add(49*a1 + 38*a2 + 20*a3 + 28*a4 + 36*a5 + 44*a6 + 85*a7 + 48*a8 +74*a9 + 73*a10 + 27*a11 + 99*a12 + 21*a13 + 72*a14 + 89*a15 +3*a16 + 3*a17 + 72*a18 + 71*a19 + 29*a20 + 92*a21 + 19*a22 +42*a23 + 87*a24 + 97*a25 + 36*a26 + 84*a27 + 56*a28 + 96*a29 +40*a30 + 82*a31 == 164206)
solver.add(a1>32, a2>32, a3>32, a4>32, a5>32, a6>32, a7>32, a8>32, a9>32, a10>32, a11>32, a12>32, a13>32, a14>32, a15>32, a16>32, a17>32, a18>32, a19>32, a20>32, a21>32, a22>32, a23>32, a24>32, a25>32, a26>32, a27>32, a28>32, a29>32, a30>32, a31>32)
solver.add(81*a1 + 88*a2 + 41*a3 + 98*a4 + 8*a5 + 70*a6 + 19*a7 + 85*a8 +
37*a9 + 64*a10 + 24*a11 + 96*a12 + 94*a13 + 78*a14 + 81*a15 +
38*a16 + 10*a17 + 87*a18 + 75*a19 + 35*a20 + 7*a21 + 98*a22 +
63*a23 + 37*a24 + 4*a25 + 40*a26 + 13*a27 + 83*a28 + 99*a29 +
61*a30 + 60*a31 == 171511)
solver.add(53*a1 + 39*a2 + 10*a3 + 36*a4 + 37*a5 + 42*a6 + 69*a7 + 66*a8 +
22*a9 + 33*a10 + 34*a11 + 4*a12 + 77*a13 + 94*a14 + 51*a15 +
87*a16 + 3*a17 + 34*a18 + 44*a19 + 17*a20 + 48*a21 + 31*a22 +
62*a23 + 15*a24 + 59*a25 + 39*a26 + 42*a27 + 48*a28 + 63*a29 +
44*a30 + 84*a31 == 131705)
solver.add(58*a1 + 53*a2 + 93*a3 + 4*a4 + 33*a5 + 76*a6 + 88*a7 + 7*a8 + 21*a9 + 24*a10 + 8*a11 + 35*a12 + 64*a13 + 54*a14 + 20*a15 + 1*a16 + 4*a17 + 42*a18 + 29*a19 + 96*a20 + 40*a21 + 22*a22 + 39*a23 + 47*a24 + 4*a25 + 42*a26 + 31*a27 + 69*a28 + 39*a29 + 6*a30 + 50*a31 == 114939)
print(solver.check())
a = solver.model()
print(a)

题目2–level_2_z3

题目来源：[GDOUCTF 2023]Check_Your_Luck | NSSCTF
这里附件就不给了
下载附件后打开一看直接给源码

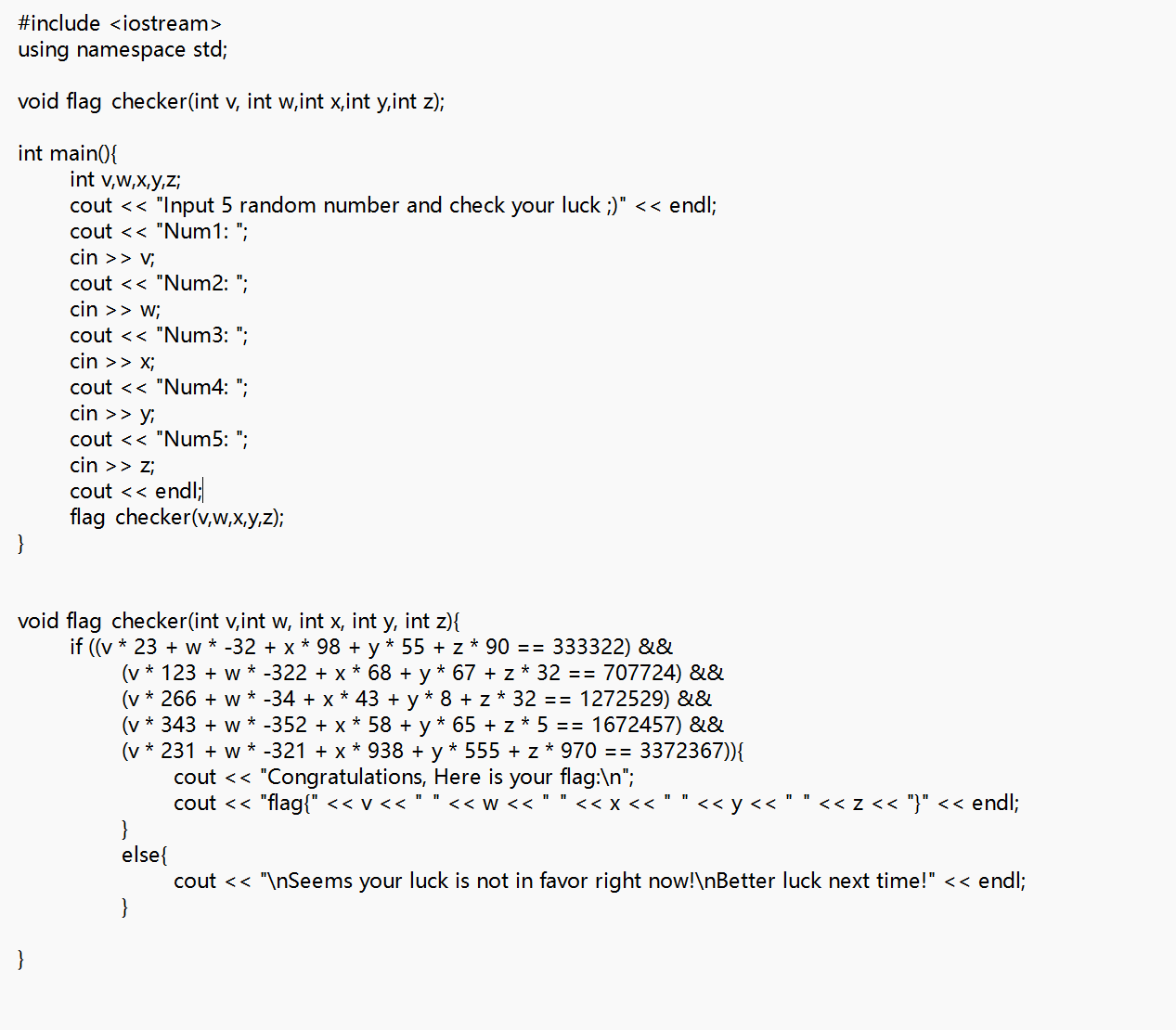
那直接就z3求解

from z3 import *
v,w,x,y,z = Ints('v w x y z')
solver = Solver()
solver.add(v * 23 + w * -32 + x * 98 + y * 55 + z * 90 == 333322)
solver.add(v * 123 + w * -322 + x * 68 + y * 67 + z * 32 == 707724)
solver.add(v * 266 + w * -34 + x * 43 + y * 8 + z * 32 == 1272529)
solver.add(v * 343 + w * -352 + x * 58 + y * 65 + z * 5 == 1672457)
solver.add(v * 231 + w * -321 + x * 938 + y * 555 + z * 970 == 3372367)
solver.check()
print(solver.model())
[x = 677, w = 123, z = 777, v = 4544, y = 1754]
NSSCTF{4544_123_677_1754_777}

angr框架

该框架就是自动逆向的一个工具，不需要手动逆向了（刚入门用不来QAQ，需要排错，还是自己手动逆吧）

介绍

angr框架是一个Python框架，angr是一个用于二进制分析工具
符号执行：
- 符号执行是一种软件测试技术
- 它不是简单地执行程序，而是在程序中的变量和表达式上使用符号值进行计算
- 在符号执行过程中，程序的每个路径都被探索，以确定输入值对程序行为的影响
- 这种技术可以帮助发现程序中的潜在错误和漏洞，同时也可以用于自动生成测试用例
安装命令pip install angr,在Linux下安装

使用

这里给出一个示例代码，仿照着写

import angr

# 创建一个angr项目，加载文件1并关闭自动加载库文件
project = angr.Project("./1",auto_load_libs=False)
# 设置文件1的初始状态为 OEP 开始运行
initial_state = project.factory.entry_state()
# 创建一个模拟器，并将设置好的初始状态添加到其中
simulation_manager = project.factory.simgr(initial_state)
# 运行模拟器，希望它走到0x400844，不希望它走到0x400855处
simulation_manager.explore(find=0x400844,avoid=0x400855)
# 如果找到可以到0x400844的路，则打印出输入 即打印出flag
if simulation_manager.found:
    print(simulation_manager.f)