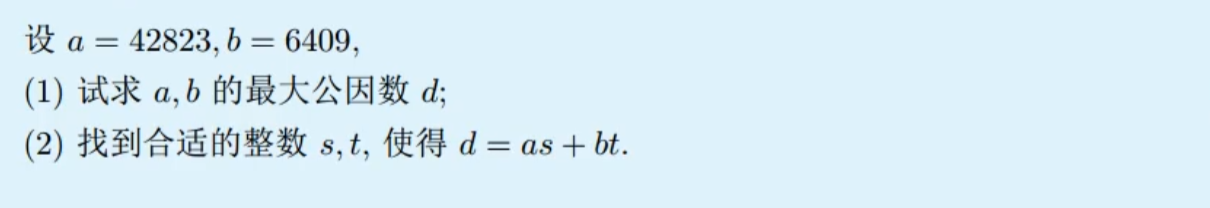• 整除与带余除法是数论的基础，贯穿整个数论，对应教材初等数论闵嗣鹤第四版，学习课程是按照这本书来的

image-20250122004858259

  • 但是上图的书太薄了，如果是硬看书的话还是看国外的这本书

image-20250126003007366

  • 对于个人的博客，顺序按照个人认为比较合理的顺序进行排序。

整除和带余除法

整除

  • 这里先介绍一下整除的定义，然后一些整除的命题和定理也进行归纳。

定义：

  • 先介绍一下整除的定义：

$$
\begin{array}{l}
设a，b∈Z，且b≠0。\
若存在q∈Z，有a = qb，则称b是a的因数（或约数），或a是b的倍数，或b能整除a，或a能被b整除。记作b|a。
\若对任意的q∈Z，有a≠qb，则称a不能被b整除，记作b∤a。
\end{array}
$$

命题：

命题1：
$$
\begin{array}{l}
设a，b∈Z，且b≠0，则有：\
1.~~ b|0 (即零是任何非零整数的倍数)\
2.~~1|a (即1是任何整数的因数)\
3. ~~当a≠0时，a|a (任何一个非0整数都是它自身的因数)
\end{array}
$$

命题2：
$$
\begin{array}{l}
设a，b，s∈Z\

  1. ~~若b|a，则b|as。\
  2. b|a当且仅当 -b|a(即a的因数总是成对出现)。\
  3. b|a当且仅当 b||a|(即a与|a|的所有因数相同)。
    \end{array}
    $$

命题3：

$$
\begin{array}{l}

  1. ~~若c|a，c∤b，则c∤(a+b)或c∤(a-b)\
  2. ~~若b|a，c≠0，则bc|ac，反之若bc|ac，则b|a\
  3. ~~若b|a，c|d则bc|ad\
  4. ~~若a=b+c，d|a，d|b，则d|c
    \end{array}
    $$

命题4：
$$
\begin{array}{l}
1.若n是正整数,a≠b,则a-b|(a^n-b^n)\
2.若n是正奇数,a≠-b,则a+b|(a^n+b^n)\
3.若n是正偶数，a≠-b,则a+b|(a^n-b^n)
\end{array}
$$

命题5（重要）：

(a,b)表示a,b两个数的最大公因数，[a,b]表示a,b两个数的最小公倍数。

对于命题5，这边先要介绍两个关于最小公倍数和最大公因数的定理。

定理1：注意这里的s、t可以是正的也可以是负的
$$
已知(a,b)=x，则存在s,t∈Z,有sa+tb=x
$$
定理2：
$$
对于[a,b]和(a,b)，满足关系:[a,b] = \frac{ab}{(a,b)}
$$

命题5如下：

$$
\begin{array}{l}
1.若c\mid ab且(b,c) = 1，则c\mid a\
2.若b\mid a，c\mid a且(b，c)=1，则bc\mid a\
3.若b\mid a，c\mid a则[b，c]\mid a
\end{array}
$$

定理：

定理1(整除的传递性)：
$$
设a，b，c∈Z，b，c≠0，则若b|a，c|b，则c|a。
$$

定理2：

$$
设a，b∈Z，都是m的倍数，则a+b或a-b也是m的倍数。
$$

定理3：
$$
设a_1,a_2,…,a_n∈Z都是m的倍数,q_1,q_2,…,q_n∈Z则q_1·a_1+q_2·a_2+…+q_n·a_n也是m的倍数
\即若m|a_i(i=1,2,…,n),q_i∈z,则m|(q1·a1+…+q_n·a_n)
$$

带余除法

  • 带余除法的定义同时也是一个定理
  • 所以这边先介绍一下带余除法的定义（定理）

$$
设a，b∈Z且b＞0，则存在唯一的两个整数q和r，使得a=bq+r\
其中0≤r＜b
$$

  • 由这个定理可以得到一个推论即：这边将b>0替换成了b≠0

$$
设a，b∈Z且b≠0，则存在唯一一对整数q和r，使得a=bq+r\
其中0≤r＜ \left | b \right |
$$

在上面的定理和推论中，q叫做a被b除的不完全商，r叫做a被b除的余数。

最大公因数与辗转相除法

例题

  • 在介绍最大公因数与辗转相除法之前，先来介绍一下最大公因数的求法

image-20241211125540630

题目1：

​ 方法一：因数分解法
$$
a=216=2^33^3\
b=128=2^7\
所以(a,b)=2^3
$$
​ 方法二：辗转相除法
$$
216÷128=1···88\
128÷88=1···40\
88÷40=2···8\
40÷8=5···0\
所以最后(a,b)=8\
\
还可以写成这样\216=1281+88
\128=881+40
\88=402+8
\40=8*5+0
\所以(a,b)=8
$$
题目2：

​ 这题只能使用辗转相除法，因为这俩个数都是质数。
$$
983=5471+436\
547=4361+111\
436=1113+103\
111=1031+8\
103=812+7\
8=71+1\
7=1*7+0\
所以(983,547)=1
$$
题目3：

​ 这题同样使用两种方法

​ 方法1：
$$
72=2^33^2\
48=2^43\
54=3^223\
所以(72,48,54)=6
$$
​ 方法2：这题是3个数的最大公因数，使用辗转相除法，我们先要求其中俩个数的最大公因数，再将该数与第三个数求最大公因数。
$$
72=481+24\
48=242+0\
(72,48)=24\
54=242+6\
24=64+0\
所以(72,48,54)=6
$$

最大公因数1

  • 接下来介绍一下最大公因数的定义

定义1：
$$
设整数a_1,a_2,…,a_n是n(n≥2)个整数\
如果整数d是它们中每一个因数,则称d为a_1,a_2,…a_n的公因数。\
$$
定义2：
$$
整数a_1,a_2,…,a_n的公因数中最大的一个称为它们的最大公因数,
\记作(a_1,a_2,…,a_n).
$$
定义3：
$$
如果(a_1,a_2,…,a_n)=1,则称a_1,a_2,…,a_n互质或互素.\
如果a_1,a_2,…,a_n中任意两个整数互质，则称它们两两互质。
$$

  • 接下来是几个命题

命题1：该命题讨论的是公因数存在性问题。
$$
\begin{array}{l}
a_1,a_2,…,a_n∈Z的公因数必定存在\
若a_1,a_2,…,a_n不全为零,则(a_1,a_2,…a_n)必定存在.\
当a_1,a_2,…,a_n不全为零时,(a_1,a_2,…,a_n)>0
\end{array}
$$

说明：

  1. 该点说明，在理论证明的时候，我们只需要考虑不全为零的最大公因数
  2. 在具体计算时，我们只考虑都不为零的整数的最大公因数
  3. 两两互质蕴含互质，但反之不成立。

注解1：这个命题可以做为最大公因数的一个证明方法
$$
\begin{array}{l}
设a_1,a_2,…,a_n为n个不全为零的整数，则(a_1,a_2,…,a_n)=d当且仅当\
(1)d\mid a_i(i=1,2,…,n);\
(2)若d’ \mid a_i(i=1,2,…,n),则d’≤d.
\end{array}
$$
注解2：该注解也给出了最大公因数的一个证明方法，本质上该方法是注解1得到的。
$$
\begin{array}{l}
d=(a_1,a_2,…,a_n)当且仅当\
(1)d\mid a_i(i=1,2,…,n);\
(2)若d’\mid a_i(i=1,2,…,n),则d’\mid d(d>0)
\end{array}
$$
在证明d’=d时就可以利用d|d’,d’|d以及，d，d‘＞0，即可得到d=d’

命题2:
$$
若b \mid a且a>0,则b≤a.
$$
​ 通过这个命题，还有一个推论：
$$
若b\mid a且a≠0,则\mid b \mid ≤ \mid a\mid
$$

  • 接下来给出最大公因数的几个性质定理：

定理1：由定理1就可以得到，如果要求一些数的公因数或者最大公因数，那么只要求这些数对应整数的公因数和最大公因数即可。
$$
\begin{array}{l}
设a_1,a_2,…,a_n为n个不全为零的整数，则\
(1)a_1,a_2,…,a_n与\left | a_1 \right |,\left | a_2 \right |,…,\left | a_n \right |的公因数相同。\
(2)(a_1,a_2,…,a_n)=(\left | a_1 \right |,\left | a_2 \right |,…,\left | a_n \right |)
\end{array}
$$

定理2：
$$
\begin{array}{l}
若b>0,且b∈Z，则:\
(1)0与b的公因数就是b的因数，反之，b的因数也是0与b的公因数\
(2)(0,b)=b
\end{array}
$$
定理2推论:
$$
若b≠0,b∈Z，则(0,b)=\left | b \right |
$$

辗转相除法

  • 之前例题介绍了辗转相除法的具体过程，接下来介绍一下概念和具体定理。

定理3（延续最大公因数的定理1和定理2）:
$$
设a,b,c是三个不全为零的整数，且a=bq+c(q≠0),
则a,b与b,c有相同的公因数,从而有(a,b)=(b,c)
$$
定理4：在介绍定理4之前先具体说一下辗转相除法。
$$
设a,b∈Z_+由带余除法：\
a=bq_1+r_1 (0≤r_1<b).\若r_1=0,则(a,b)=b,~~~~~若r_1≠0,则由定理3,(a,b)=(b,r1)\
(r1≠0),b=r_1q_2+r_2(0≤r_2＜r_1)\
若r_2=0，则(a,b)=(b,r_1)=r_1,~~~~若r_2≠0,则由定理3,(a,b)=(b,r1)=(r_1,r_2)
\…\
r_{n-1}=r_nq_{n+1}+r_{n+1},~~~~~r_{n+1}=0
\则(a,b)=(b,r_1)=…=(r_{n-1},r_n)=(r_n,r_{n+1})=(r_n,0)=r_n
$$
从而引出定理4：
$$
若a,b∈Z,则(a,b)=r_n
$$
再利用最大公因数的定理1，就可以将该式子转换为
$$
若a,b∈Z,则(a,b)=(\left | a \right |,\left | b \right |)=r_n
$$
推论:
$$
a,b的公因数与它们的最大公因数(a,b)具有相同的因数。
$$

最大公因数2

  • 接下来的定理就是一些最大公因数的运算性质了，这种运算性质可以进行抽象，抽象之后就是近世代数要研究的内容了。

定理5:定理5的运算性质就很想向量的内积的一些运算性质，可以进行类比记忆
$$
\begin{array}{l}
设a,b是任意两个不全为零的整数，则\
(1)若m∈Z_+，则(ma,mb)=m(a,b);\
(2)若\delta是a，b的一个公因数，则(\frac{a}{\delta},\frac{b}{\delta} )=\frac{(a,b)}{\delta}\
特别地,(\frac{a}{(a,b)},\frac{b}{(a,b)})=1
\end{array}
$$
注解4:
$$
(a,b)=d当且仅当存在唯一的一对互质的整数，a_1,b_1使得a=da_1,b=db_1
$$

定理6：就是例题中第3题所示的求三个数的最大公因数。由该定理就可以得到例题第3题的解法
$$
\begin{array}{l}
设a_1,a_2,…,a_n是不全为零的整数(可以假定它们都是正整数)，且\
(a_1,a_2)=d_2,(d_2,a_3)=d_3,…,~~(d_{n-2},a_{n-1})=d_{n-1},(d_{n-1},a_{n})=d_n,\
则(a_1,a_2,…,a_n)=d_n
\end{array}
$$

最大公因数3

  • 这里介绍一下最大公因数的进一步的性质。先来介绍一个定理，该定理比较重要，由该定理可以导出著名的裴蜀定理。

定理1:
$$
\begin{array}{l}
若a,b∈Z_+,则满足Q_ka-P_kb=(-1)^{k-1}r_k~~(k=1,2,…,n)\
其中\
P_0=1,P_1=q_1,P_k=q_kP_{k-1}+P_{k-2}\
Q_0=0,Q_1=1,Q_K=q_kQ_{k-1}+Q_{k-2}\
(k=2,3,…,n)
\end{array}
$$
推论1:上面定理引出的该推论就是著名的裴蜀定理。该定理在之前的证明中有使用过。
$$
\begin{array}{l}
若(a,b)=d,则存在s,t∈Z有as+bt=d.
\end{array}
$$
命题1:推理1的逆命题是不成立的，但是如果加了一些条件就会满足了。
$$
\begin{array}{l}
设a,b,d∈Z，d>0,若存在s,t∈Z,有as+bt=d,且d是a,b的公因数,则(a,b)=d.
\end{array}
$$

推论2:
$$
\begin{array}{l}
设a,b∈Z,则(a,b)=1,当且仅当存在s,t∈Z，有as+bt=1
\end{array}
$$

定理2：
$$
\begin{array}{l}
设a,b,c∈Z且(a,c)=1，则\
(1)ab,c与b,c有相同的公因数\
(2)(ab,c)=(b,c)\
这里b,c中至少有一个不为零
\end{array}
$$
推论3：
$$
\begin{array}{l}
若(a,b)=1,c\mid ab,则c\mid b
\end{array}
$$
推论4：
$$
\begin{array}{l}
设a_1,a_2,…,a_n,b_1,b_2,…,b_m是两组整数\
如果前一组的任意一个数与后一组中任意一个都互质,则a_1a_2…a_n与b_1b_2…b_m互质
\end{array}
$$

  • 这里来个例题：

image-20241213232326436

  • 接下来介绍一下其他推论、定理和命题

最小公倍数

  • 接下来介绍一下最小公倍数的定义和几个性质定理

定义：
$$
\begin{array}{l}
若e是所有a_1,a_2,…,a_n的倍数，则称e为a_1,a_2,…,a_n的公倍数\
在所有公倍数中的最小正数,叫做a_1,a_2,…,a_n的最小公倍数,记为[a_1,a2,…,a_n]
\end{array}
$$

注解:由定义引出了证明最小公倍数的方法
$$
\begin{array}{l}
[a_1,a_2,…,a_n]=e当且仅当\
(1)a_i\mid e(i=1,2,…,n);\
(2)若a_i\mid e’,则e≤e’
\end{array}
$$
定理1：
$$
\begin{array}{l}
[a_1,a_2,…,a_n]=[\left | a_1 \right |,\left | a_2 \right |,…,\left | a_n \right |]
\end{array}
$$
定理2：
$$
\begin{array}{l}
设a,b∈Z_+,\
(1)a,b的所有公倍数就是[a,b]的所有倍数;\
(2)[a,b]= \frac{ab}{(a,b)},(或a,b=ab.)\
特别地,若(a,b)=1,则[a,b]=ab
\end{array}
$$
定理3：
$$
\begin{array}{l}
若[a_1,a_2,a_3,…,a_n]=m,[a_1,a_2]=m_2,[m_2,a_3]=m_3,…[m_{n-1},a_n]=m_n,则m=m_n
\end{array}
$$

多项式带余除法

  • 最小公倍数这边引出了多项式
  • 下面给出多项式的定义并且引出多项式的带余除法

定义：
$$
\begin{array}{l}
设n∈Z_+,a_0,a_1,…,a_n∈R,a_n≠0,则称\
P(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0\
为一个n次多项式，简称多项式。
\end{array}
$$

多项式带余除法
$$
\begin{array}{l}
设P(x),M(x)是任意两个多项式,P(x)的次数大于M(x)的次数,则存在唯一的一对多项式Q(x),R(x)使得
\P(x)=M(x)Q(x)+R(x)
\其中R(x)的次数小于M(x)的次数
\end{array}
$$

算数基本定理

质数和合数

  • 质数和合数在数论中是非常重要的

定义1：质数和合数的定义：
$$
\begin{array}{l}
设p是一个大于1的整数，若它的正因数只有1及它本身，\则称p为一个质数(或素数),否则称为合数。
\end{array}
$$
注1：负数、0和1既不是质数也不是合数。

推论1：
$$
\begin{array}{l}
a是合数当且仅当存在整数1<a_1,a_2<a,有a=a_1*a_2
\end{array}
$$

  • 介绍完定义后，接下来介绍一下质数和合数相关的定理

定理1：
$$
\begin{array}{l}
设a是大于1的整数,则a的除1外的最小正因数p一定是质数,并且当a为合数时,p≤\sqrt{a}
\end{array}
$$
定理2：
$$
\begin{array}{l}
设a∈Z,p是一个质数,则p \mid a或(p,a)=1
\end{array}
$$
推论2：
$$
\begin{array}{l}
设a_1,a_2,…,a_n∈Z,p是质数\
若p\mid a_1a_2…a_n,则p能整除某一个a_i
\end{array}
$$

算数基本定理

定理3：
$$
\begin{array}{l}
任意大于1的整数都能表示为若干质数的乘积\
即若a>1,则a=p_1p_2…p_n,p1 \leq p_2 \leq …\leq p_n,其中p_i都是质数
\end{array}
$$
推论3：
$$
\begin{array}{l}
设a是大于1的整数,则a能唯一地写为a=p^{\alpha_1}1p{2}^{\alpha_2}…p_i^{\alpha_i}…p_k^{\alpha_k}
\其中\alpha_i ＞0,i=1,2,3,…,k~且~p_i<p_j
\称上式为a的标准分解式.
\end{array}
$$
注解1：对于推论3，我们可以如下变形
$$
\begin{array}{l}
在应用中,为方便计算，有时我们插进若干质数的零次幂,从而a可以表示为下面的形式\
a = p_1^{\alpha_1}p_2^{\alpha_2}…p_l^{\alpha_l},\alpha_i \geq 0,i=1,2,3,…,l
\end{array}
$$

推论4：
$$
\begin{array}{l}
设a是大于1的整数,且a=p^{\alpha_1}1p{2}^{\alpha_2}…p_i^{\alpha_i}…p_k^{\alpha_k},其中\alpha_i ＞0,i=1,2,3,…,k
\则a的正因数d可以表示为如下形式:\d=p_1^{\beta_1}p_2^{\beta_2}…p_l^{\beta_k},0\leq \beta_i\leq \alpha_i，i=1,2,3,…,k
\而且当d可以表示成上述形式时,d是a的正因数
\end{array}
$$
注解2：对于推论4，有如下结论
$$
\begin{array}{l}
设a = p_1^{\alpha_1}p_2^{\alpha_2}…p_k^{\alpha_k},\alpha_i > 0,i=1,2,3,…,k,\则a的正因数的个数有(\alpha_1+1)(\alpha_2+1)(\alpha_3+1)···(\alpha_k+1)个
\end{array}
$$

取整函数[x]

  • 先来了解一下取整函数的定义

定义：
$$
\begin{array}{l}
设x∈R,定义[x]等于不超过x的最大整数,称函数[x]为取整函数或高斯函数.
\另外也称[x]为x的整数部分,{x}=x-[x]为x的小数部分
\end{array}
$$

  • 了解定义后对于取整函数有如下的基本性质

$$
\begin{array}{l}
函数[x]，{x}具有下列性质:
\(1)~x = [x]+{x};
\(2)~[x]≤x＜[x]+1,~x-1＜[x]≤x,~0≤{x}＜1;
\(3)~设n∈Z,则[n+x]=n+[x];
\(4)~[x]+[y]≤[x+y],~{x}+{y}≥{x+y}
\(5)~~[-x] =
\begin{cases}
-[x]-1, & \text{if } x ∉ Z, \
-[x], & \text{if } x ∈ Z.
\end{cases}
\(6)~(带余除法)设a,b∈Z,b＞0,则\

\\(7)~若a,b∈Z_+,则b的倍数中小于等于a的正整数的个数为[\frac{a}{b}];
\\(8)~若x≤y,则[x]≤[y].
\end{array}
$$
  • 现在来介绍一些相关定理,这些定理是可以用基本性质推导出来的。

定理1：
$$
\begin{array}{l}
在n!的标准分解式中素因数p(p≤n)的指数h,有:
\~~~~~~~~~~~~~h=[\frac{n}{p}]+[\frac{n}{p^2}]+…=\sum_{r=1}^\infty[\frac{n}{p^r}]
\end{array}
$$
推论1：
$$
\begin{array}{l}
n!=\prod_{p≤m}p^{\sum_{r=1}^\infty[\frac{n}{p^r}]}
\其中\prod_{p≤n}表示展布在不超过n的一切素数上的乘积式.
\end{array}
$$
推论2：
$$
\begin{array}{l}
贾宪数(组合数)\frac{n!}{k!(n-k)!}(0≤k≤n)是整数,记作C^k_n~或者记作\binom{n}{k}

\end{array}
$$
推论3：
$$
\begin{array}{l}
若f(x)是一个n次整系数多项式,f^{(k)}(x)(k≤n)是它的k阶导数,
\则\frac{f^{(k)}(x)}{k!}是一个(n-k)次整系数多项式.
\end{array}
$$
定理2:
$$
\begin{array}{l}
任何k个连续整数的乘积一定能被k!整除.
\end{array}
$$

不定方程

  • 不定方程初高中都有接触过，接下来直接给出定义再给出几个例子。

定义1：不定方程
$$
\begin{array}{l}
未知数必须受到某种限制(如整数,正整数或有理数等)的方程,称为不定方程
\end{array}
$$

例子

$$
\begin{array}{l}
例1:~~x^2+y^2=z^2,其中x,y,z是正整数这就是一个不定方程
\例2:~~11x+5y=1028,其中x,y是整数,这样也就是一个不定方程
\end{array}
$$

二元一次不定方程

  • 了解了不定方程之后，接下来看二元一次不定方程的定义

定义2：二元一次不定方程
$$
\begin{array}{l}
设a,b,c∈Z,ab\neq0，则称式子\

为关于变量x,y的二元一次不定方程
\end{array}
$$
  • 了解了二元一次不定方程的概念之后，接下来一定是研究该方程如何解

定理1：二元一次不定方程的通解
$$
\begin{array}{l}
设二元一次不定方程:ax+by=c(a,b,c∈Z,ab\neq0)
\有一整数解x=x_0,y=y_0,且(a,b)=d,~a=a_1d,~b=b_1d,
\则此不定方程的一切整数解可以表示为:
\x=x_0-b_1t,y=y_0+a_1t其中t∈Z
\end{array}
$$
注意：该定理中的(a1,b1)=1，具体参考最大公因数2的注解4

证明
  • 证明这个定理需要证明两个地方：

$$
\begin{array}{l}
证明第一个地方:\x=x_0-b_1t,y=y_0+a_1t~~一定是ax+by=c的解
\证明第二个地方:\
ax+by=c的整数解,总可以表示成x=x_0-b_1t,y=y_0+a_1t
\end{array}
$$

  • 证明过程如下：

$$
\begin{array}{l}
证明1:将x=x_0-b_1t,y=y_0+a_1t代入ax+by=c可得\
a(x_0-b_1t)+b(y_0+a_1t)\
=ax_0-ab_1t+by_0+a_1bt
\ \because ax_0+by_0=c
\ \therefore ax_0-ab_1t+by_0+a_1bt=c-ab_1t+a_1bt
\又知道(a,b)=d,~a=a_1d,~b=b_1d
\ \therefore c-ab_1t+a_1bt\=c+t(a_1b-ab_1)
\=c+t(a_1b_1d-a_1b_1d)
\=c
\ \therefore x=x_0-b_1t,y=y_0+a_1t~~一定是ax+by=c的解
\end{array}
$$

$$
\begin{array}{l}
证明2:设\begin{cases}
x=x_1 \
y=y_1
\end{cases}
是ax+by=c的任意一个整数解
\end{array}
$$