背包密码加密

  • 分析一个加密算法的破解首先要比较熟悉它的加密算法以及加密体制，这样才能更好的破解背包加密。
  • 首先需要明确一点就是：超递增序列的背包密码是不抗量子的，而非超递增序列的背包密码是抗量子的。

背包问题

01背包问题

  • 在算法的动态规划中有一个比较经典的问题，就是背包问题，先来介绍一下这个问题，以此引入背包加密体制
  • 假定一个背包可以承重W，现在有n个物品，其重量分别为$a_1,a_2,…,a_n$，此时我们想知道装哪些物品可以恰好使得背包装满。并且每个物品只能被装一次。这其实就是解这样一个问题。

$$
x_1a_1+x_2a_2+…+x_na_x = W
$$

  • 其中$x_i$只能为0或者1(表示当前物品是否装进背包)。显然我们必须枚举所有的n个物品的组合才能解决这个问题，而复杂度也就是$2^n$（n个物品，每个物品都有装进背包和没装进背包，全排列就有$2^{n}$种可能，所以暴力破解最坏的情况就是遍历$2^n$种可能）

完全背包问题（简单介绍一下）

  • 假定一个背包可以承重W，现在有n个物品，每个物品的重量为$a_1,a_2,…,a_n$，并且每个物品可以无限次放入背包中，背包所有物品权重和最大是多少。

注意：01背包问题和完全背包问题的区别就在于，每个物品取的最大次数是1次还是无限次

背包加密

  • 背包问题中由于存在0、1序列，所以我们可以比较好的联想到加密的消息。

  • 在加密时，我们想要加密的明文为x，那么我们就可以将其表示为n位二进制数，然后**分别乘上$a_i$**即可得到加密结果。

  • 但是如果这个$a_{i}$没有条件限制的话，就算我们知道$a_{i}$这个密钥也没办法解密。所以为了能够解密我们就对密钥$a_{i}$进行条件的限制。

  • 超递增序列：我们规定$a_{i}$是一个超递增序列，此时我们知道密钥就可以比较容易的对背包加密后的密文进行解密。

$$
a_i>\sum_{k=1}^{i-1}a_k\
即a_i>a_1+a_2+…+a_{i-1}
$$

  • 例如：[1,2,5,11,20,41]就是一个超递增序列。
  • 但是这边就存在一个问题，我们用来加密消息的这个密钥$a_{i}$很容易被窃取或者截获，这样就会导致一个密钥的泄露。

Merkle-Hellman背包加密算法

  • 为了解决密钥泄露的问题，R. Merkle和M. Hellman在一篇论文中提出了一个非对称背包加密算法。弥补了上面背包加密的密钥泄露问题。（论文会附在后面）

  • 私钥的生成：其实私钥就是上面的$a_{i}$需要满足超递增序列，还有一个乘数w

  • 公钥的生成：

    • 公钥的生成我们需要通过模运算，进行生成，所以我们要选定一个模数m，而这个模数要大于生成私钥的和。也就是模数m需要满足如下：

    $$
    m>\sum_{i=1}^{n}a_i\
    即m>a_1+a_2+…+a_n
    $$

    • 然后我们要使用私钥w作为乘数，所以我们必须确保私钥

    $$
    gcd(w,m)=1
    $$

    • 生成了以上两个数我们就可以生成公钥，公钥生成的算法如下：

    $$
    b_i = wa_i~mod~m
    $$

    • 并将这个新的背包集$b_i$和m作为公钥。

  • 加密过程：公钥（$b_{i}$，m），私钥（$a_{i}$，w）

    • 假设我们需要加密的明文是v（已经是字符串转换为整数类型），将其转换为二进制的形式，$v_i$那么我们加密的结果为：

    $$
    c = \sum_{i=1}^{n}b_iv_i~mod~ m\
    即c = b_1v_1+b_2v_2+…+b_nv_n~mod~m
    $$

    • 我们将这个式子与上面我们更熟悉的未知量代换

    $$
    c=\sum_{i=1}^{n}wa_iv_i~mod~m=w\sum_{i=1}^{n}a_iv_i~mod~ m\
    即c = wa_1v_1+wa_2v_2+…+wa_3v_3~mod~m
    $$

  • 解密过程：

    • 首先要计算w关于m的逆元$w^{-1}$，然后通过如下的式子可以得到

    $$
    \sum_{i=1}^{n}a_iv_i~mod~m=\sum_{i=1}^{n}ww^{-1}a_iv_i~mod~m=\sum_{i=1}^{n}w^{-1}b_iv_i~mod~m=cw^{-1}~mod~m\m>\sum_{i=1}^{n}a_i\
    $$

    • 由于m是大于$a_i$的和，所以我们解密后$\sum_{i=1}^{n}a_iv_i=\sum_{i=1}^{n}a_iv_i~mod~m$，就是这么一个式子。这样我们就可以通过背包问相关的算法解密出v的二进制序列
    • 由于这个序列是超递增序列，我们的解密就可以进行如下的遍历操作，这样可以很快速的求解出最终的结果

    $$
    \begin{array}{l}
    记x = \sum_{i=1}^{n}a_iv_i,解密时已知a_i这个序列\
    x >a_n说明v_n为1,x<a_n说明v_n为0\
    当v_n为1的时候,计算得x=x-a_n\
    当v_n为0的时候,直接进行下一步操作\
    判断x >a_{n-1}说明v_{n-1}为1,x<a_{n-1}说明v_{n-1}为0\
    以此类推直到a_1
    \end{array}
    $$

    • 解密出二进制序列后就可以还原出加密的消息了。但是当加密消息的二进制序列过长的时候我们在最后还原出二进制序列的时候需要的算力就很大，这个解密的时间一定程度上会受到影响。

加解密代码实现

  • 加密过程如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from Crypto.Util.number import *
import random
import gmpy2
# 选择加密的消息flag,将消息转为整数后再转为二进制序列
flag = b'flag'
v = bytes_to_long(flag)
v = bin(v)[2:]

# 生成模数m和与m互素的私钥
m = getPrime(200)
w = getPrime(18)

# 选择一个超递增序列a,并将列表b为ai*w的序列
a = [3, 5, 15, 25, 55, 127, 231, 512, 991, 2046, 4033, 8161, 16307, 32614, 65391, 130575, 261330, 522531, 1047888, 2094999, 4192536, 8382741, 16769048, 33545618, 67086288, 134167557, 268336325, 536672015, 1073358395, 2147301026, 4294750090]
b = []
"""
total = 0
for i in range(len(v)):
    while True:
        temp = random.randint(2**(i),2**(i+2))
        if temp > total:
            total+=temp
            a.append(temp)
            break
assert m > sum(a)
assert gmpy2.gcd(w,m)==1
"""
# 计算得到bi的过程
for i in range(len(v)):
    b.append(a[i]*w)

# 对明文加密的过程
c = 0
for i in range(len(v)):
    c += int(v[i],2) * b[i]
c = c % m

print(c)
# 计算逆元
w_ = gmpy2.invert(w,m)
c = c*w_ % m
print(c)

# 验证是否相等
x = 0
for i in range(len(v)):
    x += int(v[i],2)*a[i]
assert x == c

解密代码实现

  • 由于是递增序列，所以我们可以从最高判断到最低，这样我们就可以，得到m的二进制位
  • 此时我们就可以逐二进制位对其进行解密
1
2
3
4
5
6
7
8
9
10
11
12
import libnum
a = [3, 5, 15, 25, 55, 127, 231, 512, 991, 2046, 4033, 8161, 16307, 32614, 65391, 130575, 261330, 522531, 1047888, 2094999, 4192536, 8382741, 16769048, 33545618, 67086288, 134167557, 268336325, 536672015, 1073358395, 2147301026, 4294750090]
c = 7734243960
m = ''
for i in range(len(a)-1,-1,-1):
    if c>=a[i]:
        m += '1'
        c-=a[i]
    else:
        m+='0'
m = int(m[::-1],2)
print(libnum.n2s(int(m)))

离散对数问题的背包加密

  • 在他们的论文中除了提供了上面的Merkle-Hellman背包加密算法，还提供了另一种陷门方案，就是基于离散对数问题的乘法型陷门背包。
  • 因为上面的那一种生成公钥的方式是线性生成的，所以该加密方式容易被攻击。
  • 我们也详细介绍一下这个基于离散对数问题的背包加密过程。这个加密理论可行，但是在公私钥的生成会出现问题，这就使得背包加密体制一般都指前面一种背包加密。

私钥的生成：

  • 选取一个对数底数g

  • 选取一个模数p

  • 私钥的生成就是上文中的$a_n$(需要满足$a_n$中的元素两两互素)，并且此时的$a_n$并不需要保证超递增序列，只需要保证$p>\prod_{i=1}^na_iv_i$

  • 由于我们离散对数的问题，所以建议先生成公钥，然后利用公钥反推私钥

公钥的生成：

  • 利用私钥给中的$a_n$、g、p，按照如下方式生成公钥$b_n$

$$
b_n = log_g(a_i)~mod~p
$$

加密过程：公钥（$b_n$）私钥（$a_n$，g，p）

  • 对于给定消息v，将消息v转换成整数，最后转成整数的二进制序列$v_i$
  • 接下来我们就可以对消息加密，加密过程如下：

$$
c = \sum_{i=1}^nb_iv_i=\sum_{i=1}^nlog_g(a_i)v_i~mod~p=log_g(\prod_{i=1}^na_iv_i)~mod~p
$$

解密过程：

  • 解密过程经过如下就可以得到一个门限，如果要还原成明文二进制序列就必须满足$p>\prod_{i=1}^na_iv_i$

$$
m = g^c=g^{log_g(\prod_{i=1}^na_iv_i)}~mod~p =\prod_{i=1}^na_iv_i~mod~p
$$

  • 由于解密方知道$a_n$这个序列，此时我们就可以遍历$a_n$。此时我们通过判断$a_n$中的每个元素是否能整除m，从而得到明文的二进制序列。

背包加密相关论文

  • 论文如下：

基础题型

题目1_BaseCTF2024__babypack

  • 题目来源：baseCTF2024
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *
import random
flag=b'BaseCTF{}'
m=bytes_to_long(flag)
bin_m=bin(m)[2:]
length=len(bin_m)

a=[1]
sum=1
for i in range(length-1):
    temp=random.randint(2*sum+1,4*sum)
    sum=sum+temp
    a.append(temp)

a=a[::-1]
c=0
for i in range(length):
    if bin_m[i]=='1':
        c=c+a[i]
print("a=",a)
print("c=",c)
  • 这题就是基本的Merkle-Hellman背包加密算法中的解密过程
1
2
3
4
5
6
7
8
9
10
11
12
13
import libnum
a = []
c = 2488656295807929935404316556194747314175977860755594014838879551525915558042003735363919054632036359039039831854134957725034750353847782168033537523854288427613513938991943920607437000388885418821419115067060003426834
m = ""
for i in range(len(a)):
    if c >= a[i]:
        m+='1'
        c-=a[i]
    else:
        m+='0'
m = int(m,2)
print(libnum.n2s(int(m)))
# b'BaseCTF{2c4b0c15-3bee-4e4a-be6e-0f21e44bd4c9}'

题目2_MoeCTF2022__MiniMiniBackPack

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from gmpy2 import *
from Crypto.Util.number import *
import random
from FLAG import flag

def gen_key(size):
    s = 1000
    key = []
    for _ in range(size):
        a = random.randint(s + 1, 2 * s)
        assert a > sum(key)
        key.append(a)
        s += a
    return key


m = bytes_to_long(flag)
L = len(bin(m)[2:])
key = gen_key(L)
c = 0

for i in range(L):
    c += key[i]**(m&1)
    m >>= 1

print(key)
print(c)


  • 解密脚本与题目1的一样
1
2
3
4
5
6
7
8
9
10
11
12
import libnum
a =
c =
m = ''
for i in range(len(a)-1,-1,-1):
    if c >= a[i]:
        m +='1'
        c -=a[i]
    else:
        m +='0'
print(libnum.n2s(int(m,2)))
# b'moectf{Co#gRa7u1at1o^s_yOu_c6n_d3c0de_1t}'

格攻击(低密度攻击)

攻击介绍

向量角度看背包加密

  • 由于要使用格，我们就需要使用向量角度来进行背包加密的介绍。首先我们以n维向量$\vec{v}$表示明文v的二进制序列。写成向量的形式就如下。

$$
\vec{v} = (v_1,v_2,v_3,…,v_n),v_i\in{0,1},(i=1,2,…,n)
$$

  • 背包加密的私钥，也就是一开始的这个超递增序列$a_n$，使用$\vec{a}$表示。写成向量的形式就如下图所示：

$$
\vec{a} = (a_1,a_2,a_3,…,a_n)
$$

  • 然后生成模数$p$和乘数$w$，使用$\vec{b}$表示公钥序列$b_n$，所以公钥序列$b_n$写成向量的形式就是下面的这个式子：

$$
\vec{b} = w\vec{a}~mod~p = (wa_1,wa_2,wa_3,…,wa_n)~mod~p
$$

  • 这样我们加密后的密文就可以写成向量的点乘形式，如下式子

$$
c = \vec{b}·\vec{v}=b_1v_1+b_2v_2+b_3v_3+…+b_nv_n
$$

格攻击背包加密

  • 由于私钥$a_n$是一个超递增序列，所以这就使得这个加密体制存在一定被破译的分险，并且之后由于格基规约等格技术的发展，许多背包问题的变种都被证明在实际参数下是不太安全的，这些背包加密被破解的原因基本上是特殊结构或者低密度。除了 Okamoto-Tanaka-Uchiyama (OTU) 量子背包密码体制目前还没有被攻击。

  • 在读论文的时候，有一些概念需要先介绍一下，以便于我们分析背包的复杂度等，最终目的都是帮助我们理解和使用格对背包密码进行攻击。

  • 概念：背包密度d

$$
d = \frac{n}{log_2A},其中A = max{a_1,a_2,…,a_n}
$$

  • 对于一个背包密码，我们想要判断它是否能被破解，我们首要的就是看这个背包密度d
    • 当$d<0.9408…$时，这个背包密码就可以被格基规约攻击。
    • 当$d>1$时，可以使用基于格规约的变体攻击可以成功碰撞
    • 当$0.9408…<d<1$的时候，并没有比较好的格规约的攻击方式，可能有一些算法可以解特定情况，这种情况被称为困难背包问题

常规造格

  • 常规造格如下：

$$
\begin{bmatrix}
1 & 0 & \cdots & 0 & a_1 \
0 & 1 & \cdots & 0 & a_2\
\vdots & \vdots & \ddots & \vdots & \vdots\
0 & 0 & \cdots & 1 & a_n\
0&0 & \cdots &0 &c
\end{bmatrix}
$$

证明如下：

  • 其实我们一开始只需要造如下的形式的格即可，这种形式其实就是我们的基于密钥和密文造的最初的格。

$$
\begin{bmatrix}
1 & 0 & \cdots & 0 & a_1 \
0 & 1 & \cdots & 0 & a_2\
\vdots & \vdots & \ddots & \vdots & \vdots\
0 & 0 & \cdots & 1 & a_n\
0&0 & \cdots &0 &c
\end{bmatrix}
$$

  • 记每一行为$B_i$，例如$b_1=(1,0,…,0,a_1)$，其实向量组$B$其实就是格$L(b_1,…,b_{n-1})$的一个基。
  • 而明文序列$v={v_1,v_2,…,v_n},v_i\in {1,0}$
  • 由于格是离散子群，运算具有封闭性，所以$\vec{t} = v_1b_1+b_2b_2+…+v_nb_n-b_{n+1}$，在格$L(B)$上。
  • 即$\vec{t} =(v_1,v_2,…,v_n,0)$在格$L(B)$上。根据Hermite定理可以得到$\vec{t}$是$L(B)$上最短向量。
  • 至于为什么最后常用造的格最后一行是$\frac{1}{2}$或者是$1$，具体的去看格攻击相关论文第二篇吧。

优化造格

对于背包加密，我们可以构造出$n+1$个$n+1$维向量，记这些向量为$b_i$，注意这里的$a_i$没有限制为超递增序列
$$
c = \sum_{i=1}^nv_ia_i\
b_1 = (1,0,…,0,Na_1)\
b_2 = (0,1,…,0,Na_2)\
…\
b_n = (0,0,…,1,Na_n)\
b_{n+1} = (\frac{1}{2},\frac{1}{2},…,\frac{1}{2},Nc)\
$$
将上面这些向量组合成一个如下的矩阵(左边)，还可以乘个2构造如下矩阵(右边)：
$$
L(B) =
\begin{bmatrix}
1 & 0 & \cdots & 0 & Na_1 \
0 & 1 & \cdots & 0 & Na_2\
\vdots & \vdots & \ddots & \vdots & \vdots\
0 & 0 & \cdots & 1 & Na_n\
\frac{1}{2}&\frac{1}{2} & \cdots &\frac{1}{2} &Nc
\end{bmatrix}

\leftrightarrow

\begin{bmatrix}
2 & 0 & \cdots & 0 & Na_1 \
0 & 2 & \cdots & 0 & Na_2\
\vdots & \vdots & \ddots & \vdots & \vdots\
0 & 0 & \cdots & 2 & Na_n\
1&1 & \cdots &1 &Nc
\end{bmatrix}
$$

  • $a_i$和$c$前面的N是：缩放因子，放大最后一列，控制格结构。一般我们造格，N取1就行。如果N取1规约不出来的话我们就可以调整N，此时其选取范围应为$N>\frac{1}{2}\sqrt{n}$

  • 如果我们造的格是左边矩阵（存在$\frac{1}{2}$）我们规约出来的结果，如果满足这样的形式就说明是我们要找的消息二进制序列。具体值需要根据情况进行分析，该情况只是分析逐二进制序列加密，下图是论文给出的相应地方

$$
v’ = (v’_1,…,v’_2,0)\in L(B),v’_i = v_i-\frac{1}{2}
\即v’ = (v’_1,…,v’_2,0)\in L(B),v’_i\in {\frac{1}{2},-\frac{1}{2}}
$$

image-20250528171520111

  • 如果我们造的是格是右边的那种矩阵，规约出来的结果就如下

$$
v’ = (v’_1,…,v’_2,0)\in L(B),v’_i = 2v_i-1\
\即v’ = (v’_1,…,v’_2,0)\in L(B),v’_i\in {1,-1}
$$

例题

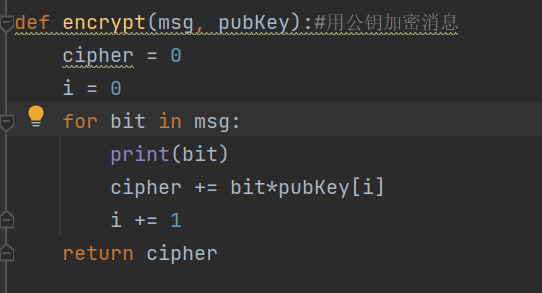
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from random import randint
from Crypto.Util.number import bytes_to_long,long_to_bytes,GCD,inverse
from secret import flag
def bitlength(n):#判断消息长度
	length=len(bin(bytes_to_long(n))[2:])
	return length
def makeKey(n):#生成超递增序列，得到私钥、公钥
	length=len(n)
	privKey = [randint(1, 65536**length)]
	sum = privKey[0]
	for i in range(1, length):
		privKey.append(randint(sum*255 + 1, 65536**(length + i)))
		sum += privKey[i]
	q = 255*randint(privKey[length-1] + 1, 2*privKey[length-1])
	r = randint(1, q)
	while GCD(r, q) != 1:
		r = randint(1, q)
	pubKey = [ r*w % q for w in privKey ]#将超递增序列变为非超递增序列，作为公钥
	return privKey, q, r, pubKey

def encrypt(msg, pubKey):#用公钥加密消息
	cipher = 0
	i = 0
	for bit in msg:
		cipher += bit*pubKey[i]
		i += 1
	return cipher

def decrypt(cipher, privKey, q, r):#用私钥求得超递增序列并解密
	d = inverse(r, q)
	msg = cipher*d % q
	res = b''
	n = len(privKey)
	for i in range(n - 1, -1, -1):
		temp=0
		if msg >= privKey[i]:
			while msg >= privKey[i]:
				temp=temp+1
				msg -= privKey[i]
			res =  bytes([temp]) + res
		else:
			res =  bytes([0]) + res 
	return res
privKey, q, r, pubKey=makeKey(flag)
cipher=encrypt(flag,pubKey)
f=open("pubKey.txt",'w')
f.write(str(pubKey))
f.close()
f=open("cipher.txt",'w')
f.write(str(cipher))
f.close()
print(decrypt(encrypt(flag,pubKey),privKey,q,r))
assert decrypt(encrypt(flag,pubKey),privKey,q,r)==flag
  • 查看代码我们会比较清楚这个背包加密的过程其实就是Merkle-Hellman背包加密算法。生成超递增序列作为私钥。

$$
生成私钥privkey_n满足privkey_k >\sum^{k-1}{i=1}\
生成乘数r,模数p,公钥pubkey=privkey*r~mod~p\
$$

  • 但是在加密的时候有所不同，不同的地方在于，Merkle-Hellman背包加密算法使用的是二进制序列去乘每个公钥，而我们的这个加密是使用flag的ASCII码直接去乘公钥。

$$
c = \sum_{i=1}^{n}ord(m_i)*pubkey_i
$$

image-20250528170851712

image-20250528170900968

  • 很显然是经典的背包加密，并且我们已知公钥和密文，所以我们就使用经典的造格，对所造之格进行规约。

$$
\begin{bmatrix}
1 & 0& \cdots &0 &pubkey_1\
0 & 1& \cdots&0 &pubkey_2 \
\vdots &\vdots&\ddots&\vdots&\vdots\
0 &0&\cdots&1&pubkey_n\
0 &0&\cdots&0&c\
\end{bmatrix}
$$

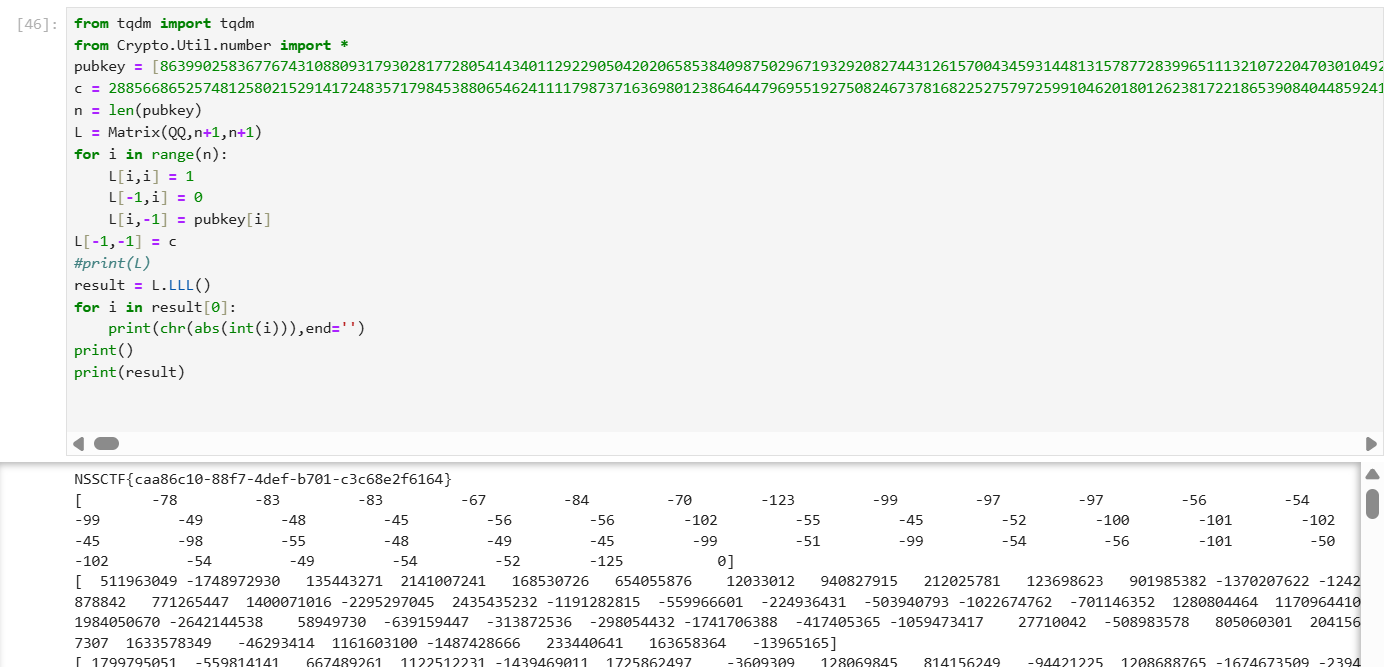
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from tqdm import tqdm
from Crypto.Util.number import *
pubkey = 

n = len(pubkey)
L = Matrix(QQ,n+1,n+1)
for i in range(n):
    L[i,i] = 1
    L[-1,i] = 0
    L[i,-1] = pubkey[i]
L[-1,-1] = c
#print(L)
result = L.LLL()
for i in result[0]:
    print(chr(abs(int(i))),end='')

  • 最终规约出来的结果如下：

image-20250528171159958

  • 但是如果我们这样造格，规约出来的结果m需要$m//2+1$，才能得到最终的明文，

$$
\begin{bmatrix}
2 & 0& \cdots &0 &pubkey_1\
0 & 2& \cdots&0 &pubkey_2 \
\vdots &\vdots&\ddots&\vdots&\vdots\
0 &0&\cdots&2&pubkey_n\
1 &1&\cdots&1&c\
\end{bmatrix}
$$

格攻击相关论文

  • 这篇论文是介绍背包攻击的几个方法，其中就包含了格攻击，细读之后发现该论文只是介绍方法，已经怎么造格，并没有具体的证明。
  • 对于格攻击的具体证明，即证明消息的二进制序列构成的向量是那个格中的最短向量。

题目1_

题目2_

题目3_hgame2025_ezBag

$$
\begin{bmatrix}
x_1&x_2&\dots&x_{n-1}&x_{n}&-1&-1&-1&-1
\end{bmatrix}
*
\begin{bmatrix}
2&0&\dots&0&0&list[0]1&list[1]1&list[2]1&list[3]1\
0&2&\dots&0&0&list[0]2&list[1]2&list[2]2&list[3]2\
\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\
0&0&\dots&2&0&list[0]{63}&list[1]{63}&list[2]{63}&list[3]{63}\
0&0&\dots&0&2&list[0]{64}&list[1]{64}&list[2]{64}&list[3]{64}\
1&1&\dots&1&1&bag[0]&0&0&0\
1&1&\dots&1&1&0&bag[1]&0&0\
1&1&\dots&1&1&0&0&bag[2]&0\
1&1&\dots&1&1&0&0&0&bag[3]\
\end{bmatrix}
$$

题目4_LitCTF_new_Bag

参数不当