• 对于加密按照对加密数据的处理可分为流加密和块加密，块加密的算法一般都在对称加密中体现，而这里只介绍块加密工作模式，以及相应的攻击。

  • 块加密的工作模式分为以下几类：ECB模式、CBC模式、CTR模式、CFB模式、OFB模式、GCM模式，接下来逐一介绍这些工作模式的具体过程。以及这些模式的相关攻击，有些攻击会有对应的CTF题目为例题。

  • 下面这些块加密模式都以AES块加密算法为例子，我们并不需要具体了解AES加密算法的过程。

明文处理

  • 对于块加密，我们都要对明文进行分组处理，既然对明文要分组处理，这就会导致分得的最后一组会存在不足，此时我们就要用特定的数据对分组后的明文进行填充操作
  • 块加密的分组方式一般还取决于块加密的一些算法，比如使用AES加密算法一般就是将明文分为128位为一组，而使用DES加密一般就是将明文分为64位为一组
  • 所以我们一开始会对明文进行如下的分组处理：
    • 明文被分成固定大小的块（每块多少位取决于加密算法）
    • 如果明文长度不是块大小的整数倍，最后一个块需要填充（通常使用PKCS#7填充）
    • 注：有些填充方式如果明文长度是块大小的整数倍，那么最后还要填充一整块。
  • 接下来简单介绍一下一些填充方式：
    • PKCS#7(最常用)：补多少字节就填充该字节的值，比如最后一块差3个字节才满，此时就要补3个0x03。如果是要填充一整块的话，假设每块16字节，此时就要填充16个0x10。该填充方式在满足明文长度是块大小整数倍的时候还要填充一整块
    • ISO/IEC 7816-4：在尾部填充一个0x80，然后剩下的填充0，在明文长度是块大小整数倍的时候还要填充一整块。
    • ANSI_X.923：全部填充0x00，最后一个字节填充差的长度，比如差4个字节需要这样填充0x00 0x00 0x00 0x04在明文长度是块大小整数倍的时候还要填充一整块。
    • Zero_Padding：填充部分全部填充0x00，并且在明文长度是块大小整数倍的时候不需要额外填充一整块
    • ISO_10126(已弃用)：填充的时候全部填充随机数，只有最后一个字节填充差的长度(类似于ANSI_X.923)，在明文长度是块大小整数倍的时候还要填充一整块。

ECB模式

工作方式

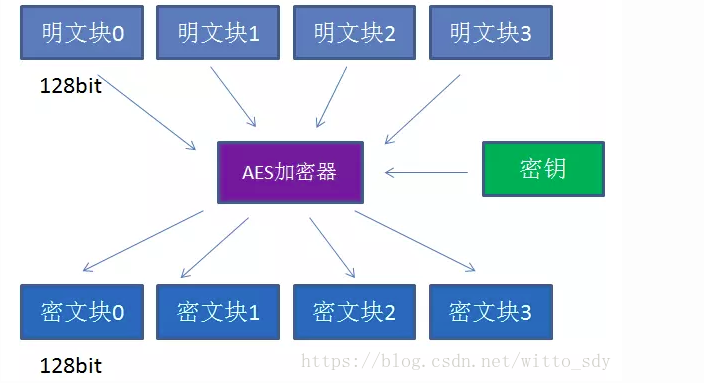
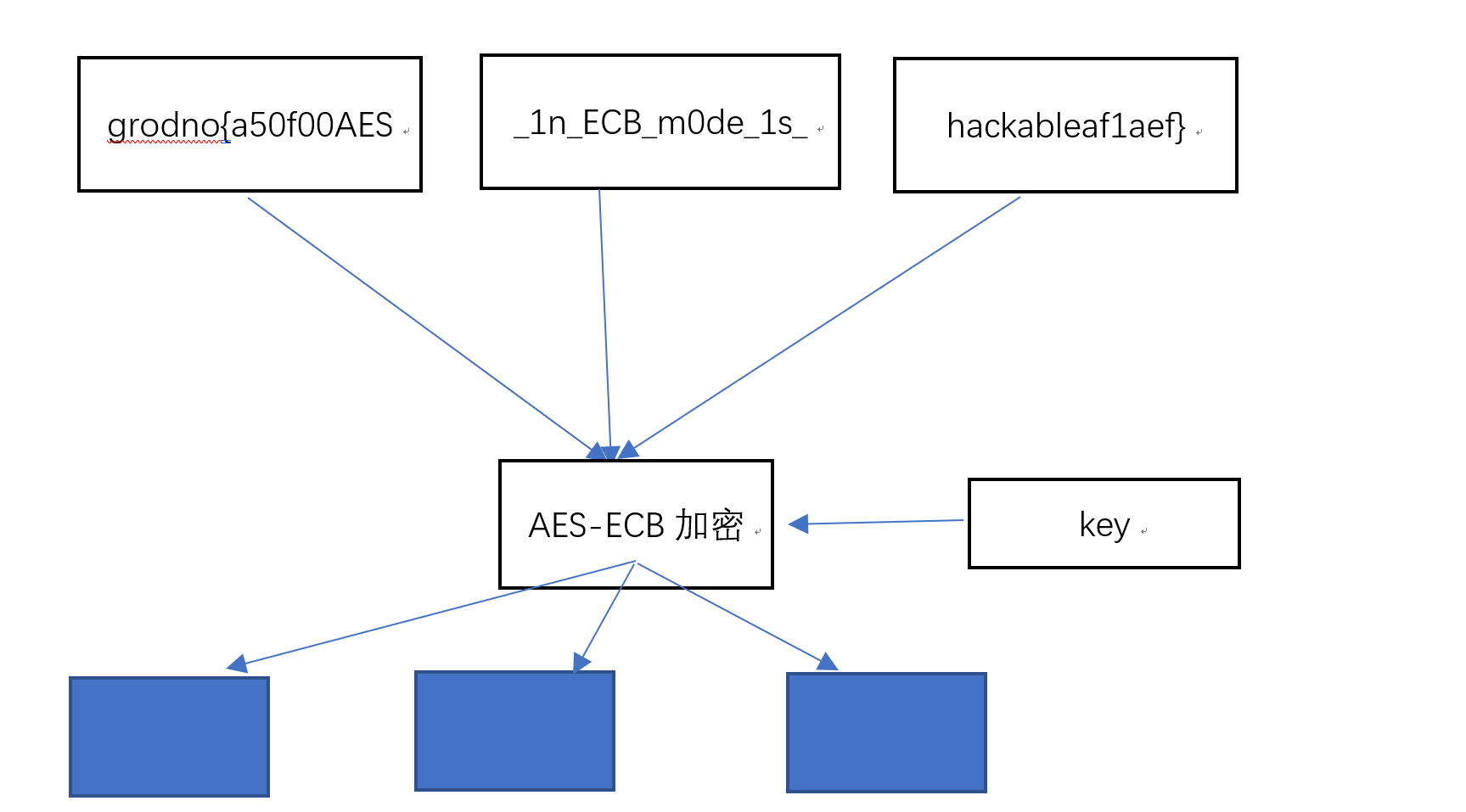
AES-ECB加密首先输入明文，首先将这些明文转化为16进制的ASCII值；其次将这些明文以16字节为一组进行分块处理。如果明文的字节数不是16进制，那么就会将最后一块明文块，按照某种填充方式，使其达到16字节。

image-20250618015927172

接下来就是使用AES加密对每一个明文块单独加密，明文块与明文块之间相互独立。

然后明文块再与密钥一起，经过AES加密，输出密文块。密文块同样也是128bit

image-20250618020037783

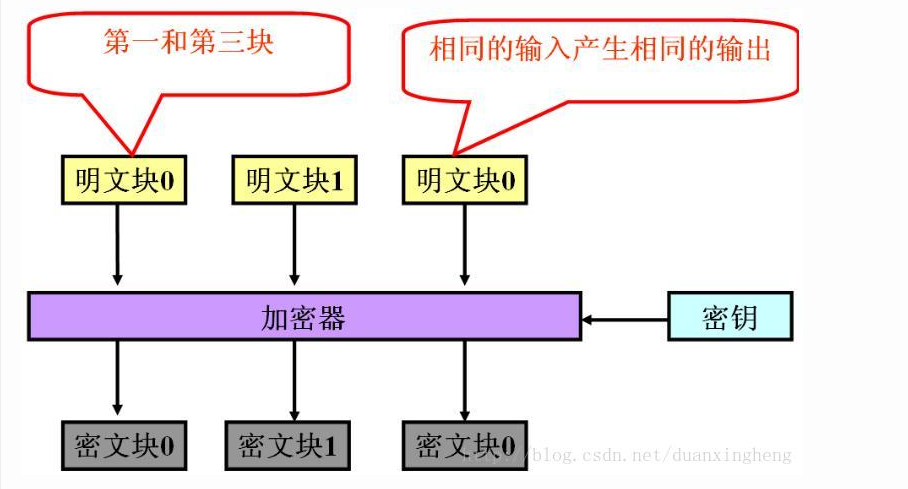
注意：ECB加密模式要注意的是，每个明文块都是使用相同的密钥进行加密的。这也就是说相同的明文会输出相同的密文。

image-20250618020105293

  • 总结：ECB的工作模式其实就是这么简单，就是利用加密算法，对每一个明文块单独加密，明文块与明文块之间相互独立，没有什么联系。所以ECB这种简单的块加密方式就非常容易被选择明文攻击

选择明文攻击

  • 该方法是利用相同的明文块经过加密后，会产生相同的明文块。这样就可以进行逐个字节的爆破，从而得到flag

  • 这里直接以CTF题入手，题目描述如下：

image-20250618020445058

  • 中文翻译过来如下：

image-20250618020456679

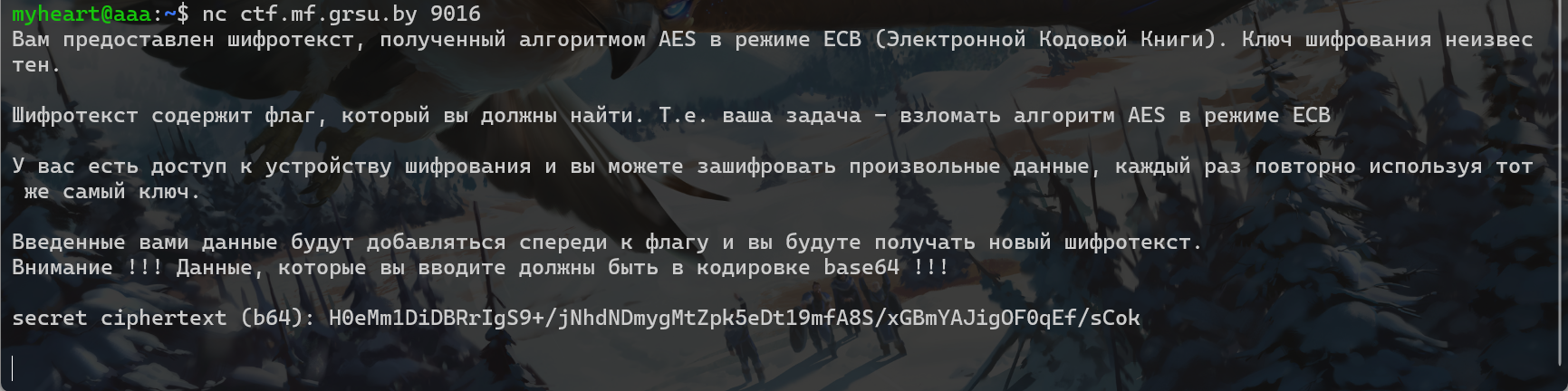
  • 先nc一下连接靶机，看看靶机上的程序是如何运行的，发现nc过后系统会将flag经过AES-ECB加密后的密文输出过来

image-20250618020529553

  • 然后再看密文上面的字，可以得到信息，用户可以输入base64编码的数据，然后靶机会重新加密，并输出重新加密过后的密文

image-20250618020546785

确定明文个数

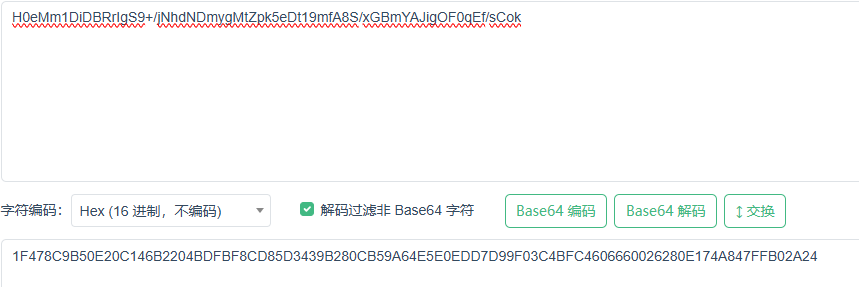
  • 所以我们可以进行如下攻击，首先确定明文个数，先将得到的密文进行base64解码，解码成16进制的形式

image-20250618020640151

  • 然后以两个十六进制数为1组，进行加密的明文一共有多少字节多少块。发现密文解码后一共有48个字节，所以按照16字节为一组的明文块，一共就有3块。初步得出明文flag的长度在32-48字节字节
1
2
3
a = '1F478C9B50E20C146B2204BDFBF8CD85D3439B280CB59A64E5E0EDD7D99F03C4BFC4606660026280E174A847FFB02A24'
print(len(a)//2)
# 48
  • 然后再进行明文填充，先输入a查看密文字节数有没改变，如果没有改变再输入aa。如果还是没有改变继续增加a的个数，然后输入进去，再检查发送过来的密文字节数
  • 这里发现当发送一个a过后密文的字节数就改变了，这就可以得到明文flag的长度为47个字节这里为什么为47个字节，而不是48个字节，是与明文块的填充方式有关
1
2
3
4
5
a
YQ==
Ox9sMgy8iPF+LWBlBwtjJGBSmwwwbV7xXyxQlUuyTQ3FLNVyTeQw42geSIGnLBj7YS+OVO/90ZQVLsGHBSULcQ==
3B1F6C320CBC88F17E2D6065070B632460529B0C306D5EF15F2C50954BB24D0DC52CD5724DE430E3681E4881A72C18FB612F8E54EFFDD194152EC18705250B71
64字节

image-20250618020739115

爆破明文原理

  • 然后确定了明文长度，就可以通过相同明文加密后的密文是相同的进行逐个字节爆破，最后得到flag。
  • 逐个字节爆破过程如下，这里为了更好的演示就直接利用本题flag进行爆破演示，从而得到flag
1
grodno{a50f00AES_1n_ECB_m0de_1s_hackableaf1aef}

image-20250618020818179

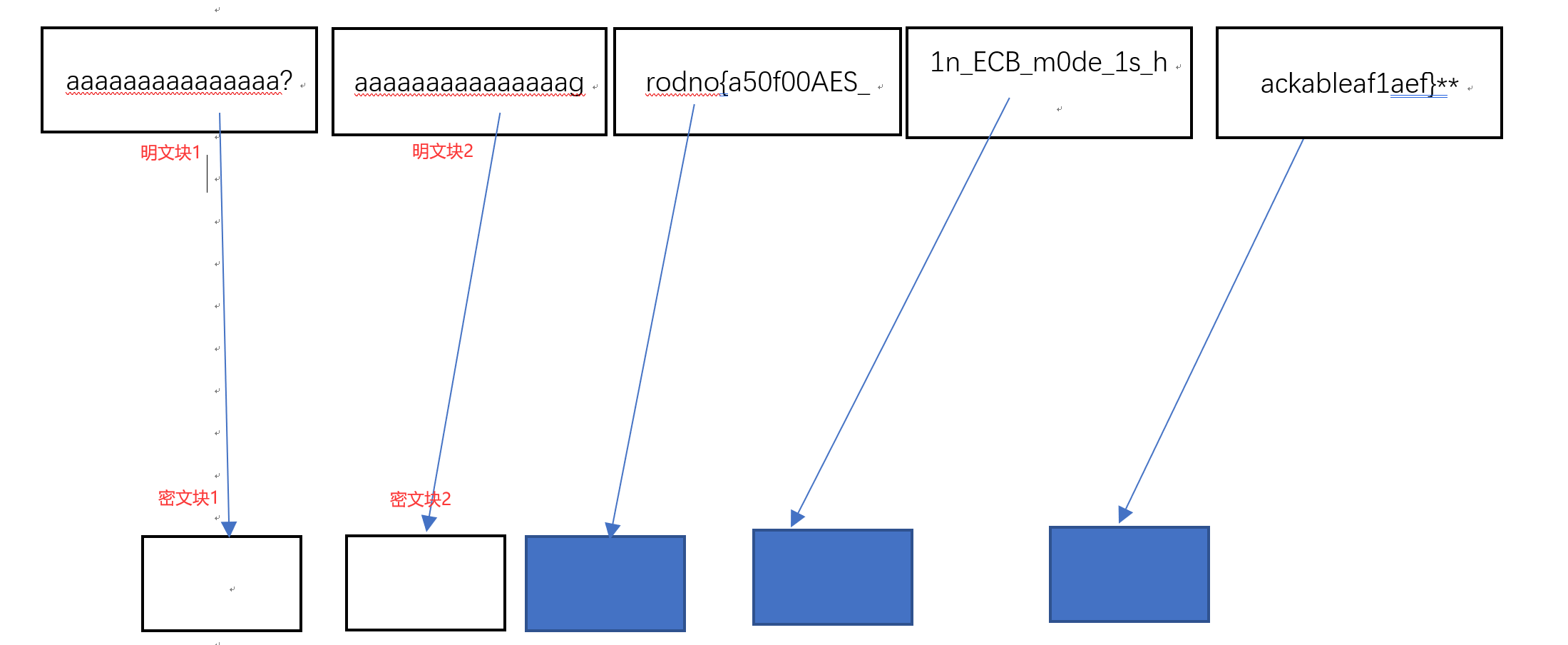
  • 爆破过程如下，先构造payload='aaaaaaaaaaaaaaa?(可见字符)aaaaaaaaaaaaaaag'
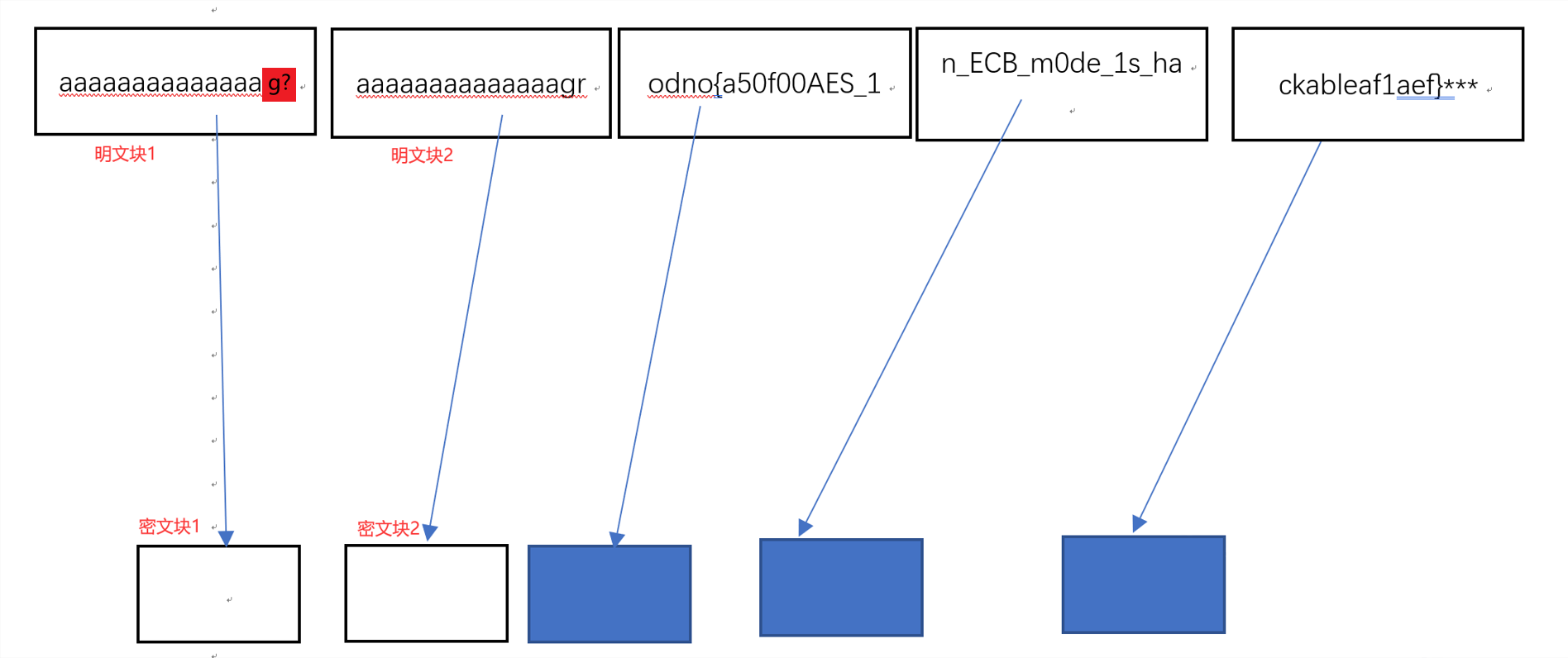
  • 然后对发送出来的密文块1，密文块2进行判断是否相同，如果相同即可得出可见字符(?)对应的字符是g，那么flag第一个字符就给爆破出来了

image-20250618020841374

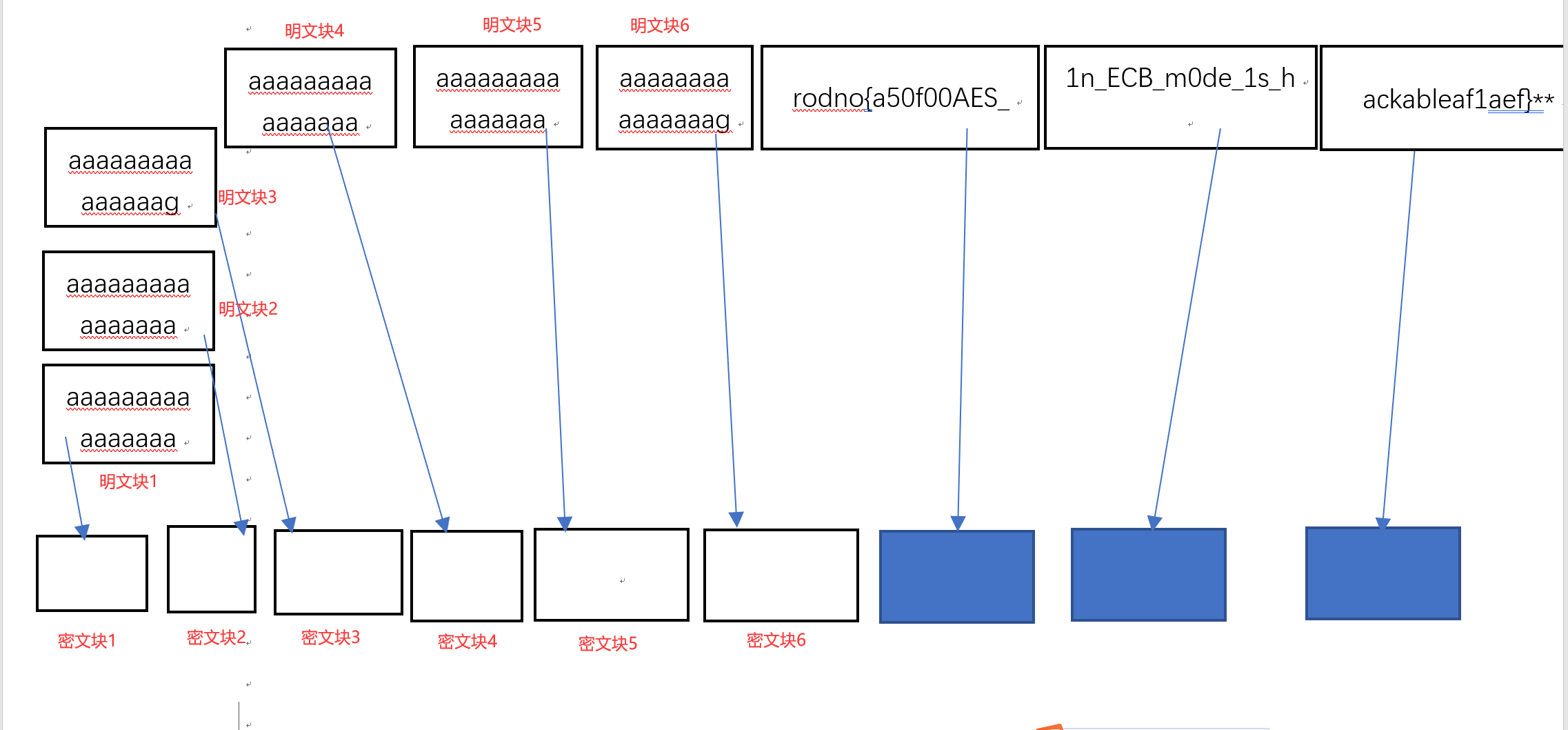
  • 然后再进行第二个字符的爆破，之后就这样重复爆破下去

image-20250618020855739

exp

  • exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from pwn import *
import base64
from Crypto.Cipher import AES
import string
def recv():
    p.recvuntil(b'ciphertext (b64): ')
    return base64.b64decode(p.recvline().strip())
def send(m):
    p.sendline(base64.b64encode(m.encode('utf-8')))
p = remote('ctf.mf.grsu.by',9016)
p.recvuntil(b'secret ciphertext (b64): ')
enc_flag = base64.b64decode(p.recvline().strip())
print(enc_flag)
charr = string.printable
l = b'a'
length= 48
flag = ''
for i in range(47):
    for ch in charr:
        send('a'*(length-1)+flag+ch+'a'*(length-1))
        res=recv()
        panduan = res[:48]
        en = res[48:96]
        if panduan==en:
            flag+=ch
            length-=1
            print(flag)
            break
print(flag)

image-20250618020930322

CBC模式

工作方式

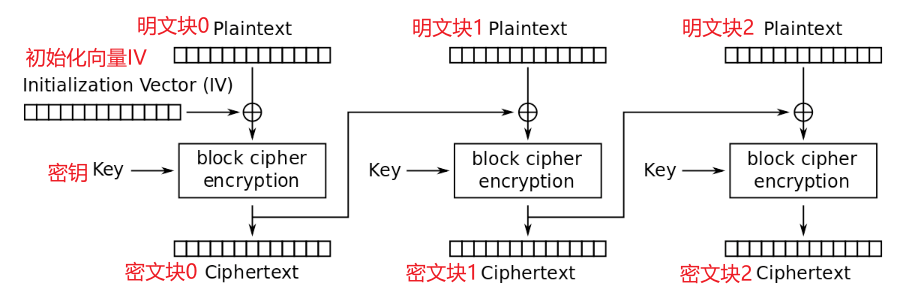
  • CBC的工作方式如下图所示：
    • 除了明文块、加密算法、密文块、密钥，还多出来了一个初始向量IV，由于AES-ECB模式块与块之间是没有关系的，这就导致了被攻击的可能性增大，而AES-CBC模式会使得块与块之间存在联系
    • 首先明文块0先于初始化向量IV进行异或操作得到中间块0
    • 接着中间块0就会被加密器使用密钥进行加密从而得到密文快0
    • 然后密文块0就会被当做类似于初始化向量IV，将密文块0与明文块1进行异或操作得到中间块1
    • 这样中间块1就会被加密器使用密钥加密成密文块1

image-20250707195422871

加密过程使用数学公式表达如下，P表示明文，C表示密文，下标0、i-1、i为区块索引编号：

C0=IVCi=Ek(Pi⊕Ci−1)C_0=IV\\ C_i =E_k(P_i\oplus C_{i-1})

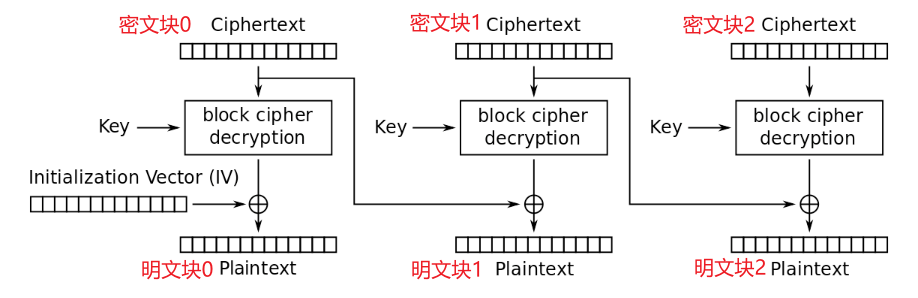
  • 解密过程如下：
    • 由于CBC模式块与块之间是有联系的，但是每个密文块(除了第一个密文块之外)其实都与前一个密文块有关系(并不是与名文块有关系)，所以在解密的过程中其实还是可以并行解密的
    • 首先密文块0被解密器使用密钥解密，得到中间块0
    • 接着中间块0与初始化向量IV进行异或操作从而得到明文块
    • 而密文块1被解密器使用密钥解密，得到中间块1
    • 中间块1再通过与密文块进行异或操作其实就可以得到明文块1以此类推下去。

image-20250707195558672

解密过程使用数学表达式如下：

C0=IVPi=DK(Ci)⊕Ci−1C_0=IV\\ P_i =D_K(C_i)\oplus C_{i-1}

密文填充攻击(Padding Oracle)

参考文章：AES-CBC密文填充攻击—深入理解和编程实现 | 网络热度

参考文章：Padding Oracle攻击解密AES - poziiey - 博客园

Padding Oracle Attack是由Vaudenay在Eurocrypt 2022首次提出。由于要满足块加密16字节为一块，通常最后一块可能不能被填满，这时就需要使用一些填充规则进行填充操作。并且将密文发送回服务器解密时，如果解密后不满足填充规则服务器会给出填充错误的提示。这就导致可以进行Padding Oracle Attack

  • 利用前提条件：

    • 需要采用PKCS5这个填充标准，填充值为需要填充的字节数。
    • 使用AES-CBC加密算法
    • 攻击者需要获得密文，以及初始向量IV
    • 攻击者可以通过服务器知道padding是否正确

  • 攻击效果：可以在未知key的条件下解出密文

  • 这里直接模拟一个加密和验证padding的服务这样更有利于理解padding Oracle attack，使用Python编写如下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from Crypto.Cipher import AES
import sys
import random
import os
flag = "flag{test_flag}"
# flag is in A-Z、a-z、{}、_
class Padding_Oracle:

    def __init__(self,text):
        self.key = os.urandom(16)
        self.cipher = AES.new(self.key,AES.MODE_CBC)
        self.chall = text.encode('utf-8')

        self.iv = os.urandom(16)

    def pad(self,s):
        padbit = 16 - len(s) % 16
        padding = bytes([padbit] * padbit)
        return s + padding

    def get_chall(self):
        aes = AES.new(self.key,AES.MODE_CBC,self.iv)
        return self.iv+aes.encrypt(self.pad(self.chall))

    def unpad(self,s):
        padbit = s[-1]
        padding = s[-padbit:]
        if set(padding) == {padbit}:
            return s[:-s[-1]]
        else:
            return None

    def decrypt(self,ciphertext):
        cipher = AES.new(self.key,AES.MODE_CBC,self.iv)
        plaintext = cipher.decrypt(ciphertext)

        return plaintext

    def oracle(self,ciphertext):
        plaintext = self.decrypt(ciphertext)
        if self.unpad(plaintext) == None:
            return False
        else:
            return True

if __name__ == "__main__":
    print("Welcome to Padding oracle attack!!!")
    oracle = Padding_Oracle(flag)
    print(oracle.get_chall().hex())
    print("begin your attack")
    while True:
        ciph = bytes.fromhex(input("ct:"))
        if len(ciph) % 16 != 0:
            print("ct must be a multiple of 16 bytes.")
            continue
        print("Oracle says: ", oracle.oracle(ciph))

# 可以直接使用Docker搭建密码学交互靶机在本地进行实验

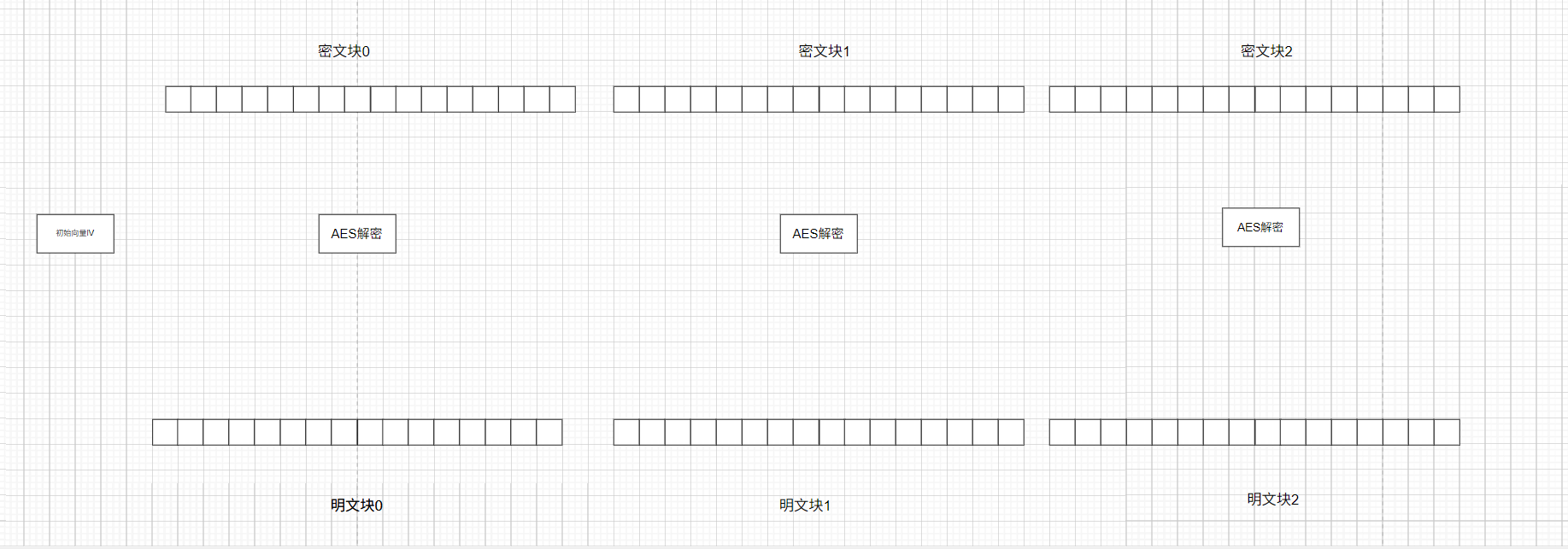
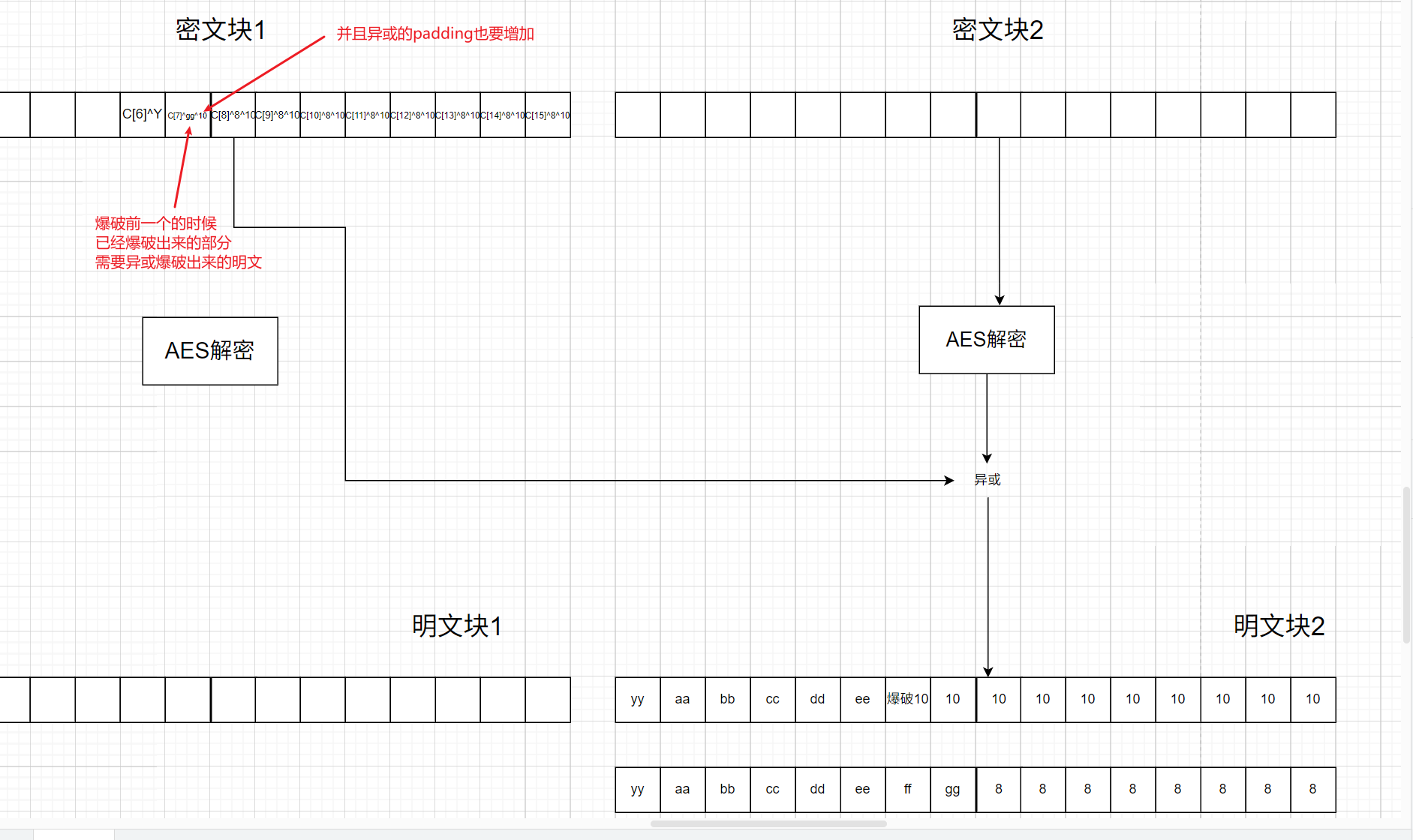
接下来配合着公式和图片进行讲解，如下图所示，图片中是一个明文被分为三组进行加密操作，所以在破解的时候我们需要破解三部分分别是最后一部分(即存在padding的块)、中间部分(一般情况下的块)、开头部分(即与初始向量iv进行异或的块)

image-20250707202051964

如果发送方使用PKCS #7格式填充，则接收方需要先解密所有密文块、验证尾部填充符合PKCS #7规范，随后移除填充，最后返回解密后的明文信息给应用程序。 **为了系统容错和调试的需要，接收方（服务器端）的实现在验证填充失败时，常常返回特定的“填充无效”出错代码。**这本是为方便系统管理员和用户的一个设计，可就是这一功能成为被攻击者利用来实现密文破解的突破口。

确定密文和IV

  • 从下面这段代码中，我们发现当我们使用nc连接的时候，靶机会将iv和密文都发送给我们。
1
2
3
def get_chall(self):
    aes = AES.new(self.key,AES.MODE_CBC,self.iv)
    return self.iv+aes.encrypt(self.pad(self.chall))

image-20250707202337402

  • 所以先要分离iv和密文，并且需要对密文进行分组由于发送过来的是16进制字符，所以以32个十六进制字符为一组就可以分离出IV和密文，同时还可以对密文进行分组操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from pwn import *
import string
context.log_level='debug'
p =  remote("ip",9002)
p.recvuntil(b'Welcome to Padding oracle attack!!!\n')
c1 = p.recvline()[:-1].decode()
print(c1)
iv = c1[:32]
c2 = c1[32:]
print('密文:',c2)
print('初始化向量IV:',iv)
l = len(c2)
ll = l//32
#print(l)
print("密文可分组数:",l//32)
c_list = []
for i in range(ll):
    c_list.append(c2[i*32:i*32+32])
print("分组后的密文:",c_list)

image-20250707203625574

最后一块填充块

  • 确定了密文和IV后，再来看程序接收用户发送的密文后的界面过程。
    • 先来看oracle函数该函数会将用户发送到服务端的密文进行解密。
    • 还会将解密后的密文进行unpad处理，并判断unpad处理的结果是正确还是错误
    • 如果unpad处理发现填充不对，就说明用户发送的数据有错误或者数据可能被篡改，并告诉用户false
    • 由于程序会告诉用户false，并且用户可以无限次发送数据，这就使得用户可以爆破pad，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def unpad(self,s):
    padbit = s[-1]
    padding = s[-padbit:]
    if set(padding) == {padbit}:
        return s[:-s[-1]]
    else:
        return None
    
def decrypt(self,ciphertext):
    cipher = AES.new(self.key,AES.MODE_CBC,self.iv)
    plaintext = cipher.decrypt(ciphertext)

    return plaintext

def oracle(self,ciphertext):
    plaintext = self.decrypt(ciphertext)
    if self.unpad(plaintext) == None:
        return False
    else:
        return True
    
if __name__ == "__main__":
    print("Welcome to Padding oracle attack!!!")
    oracle = Padding_Oracle(flag)
    print(oracle.get_chall().hex())
    print("begin your attack")
    while True:
        ciph = bytes.fromhex(input("ct:"))
        if len(ciph) % 16 != 0:
            print("ct must be a multiple of 16 bytes.")
            continue
        print("Oracle says: ", oracle.oracle(ciph))

0x1确定尾块填充的长度：

对于最后一个区块（即尾块）CnC_n，可以肯定的是它一定包含填充，最少1个0x1，最,16个0x10（参考前面的PKCS#7填充）。攻击者其实就可以从Cn−1C_{n-1}(即尾块的前面一个块)的左边第一个字节开始，将其修改成（下面都使用10进制表示，因为16进制0x在Latex中x会被修饰成更像符号的东西）

Cn−1′[0]=Cn−1[0]⊕16C'_{n-1}[0] = C_{n-1}[0]\oplus 16

image-20250707210355315

然后我们将Cn−1′与CnC'_{n-1}与C_n一起发送给接收方。接收方在执行AES-CBC解密的时候会先得到中间块XnX_{n}，此时解密后的Pn′P'_n，原始明文为PnP_n就会有如下式子：

\begin{align*} P_n'[0] &= X_n[0] \oplus C_{n-1}[0] \\ &= X_n[0] \oplus (C_{n-1}[0] \oplus 16) \\ &= (X_n[0] \oplus C_{n-1}[0]) \oplus 16 \\ &= P_n[0] \oplus 16 \end{align*}

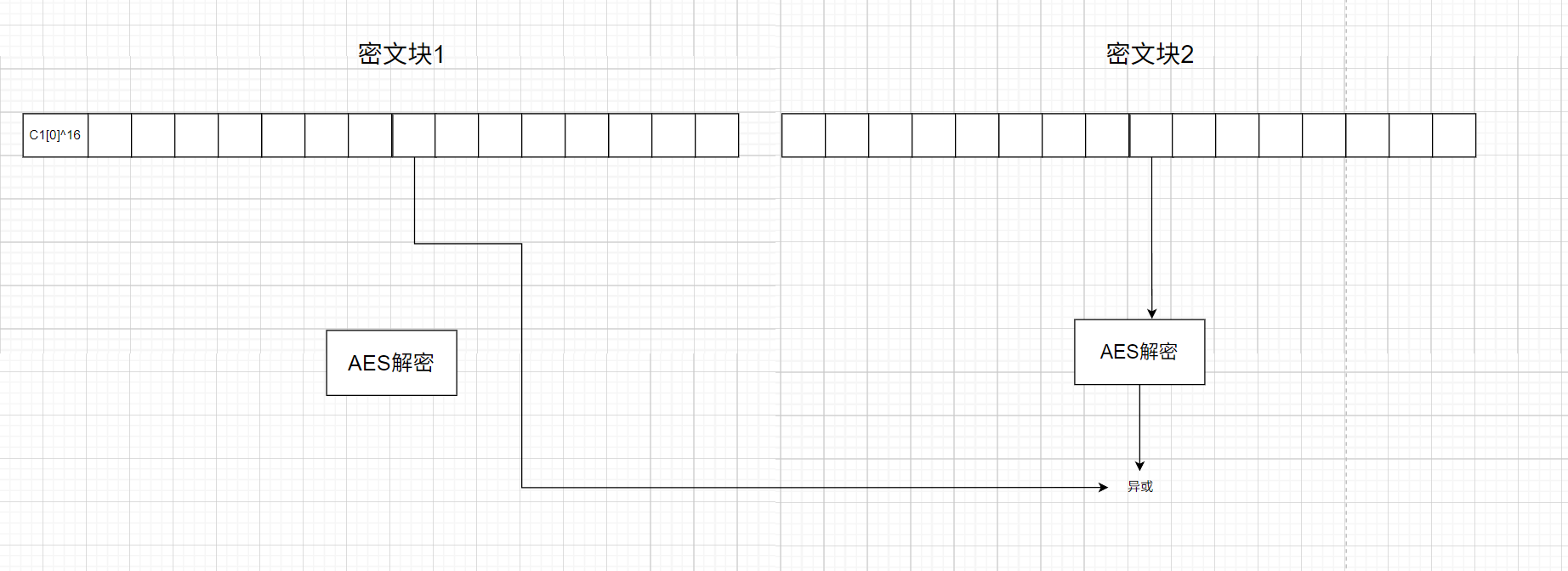
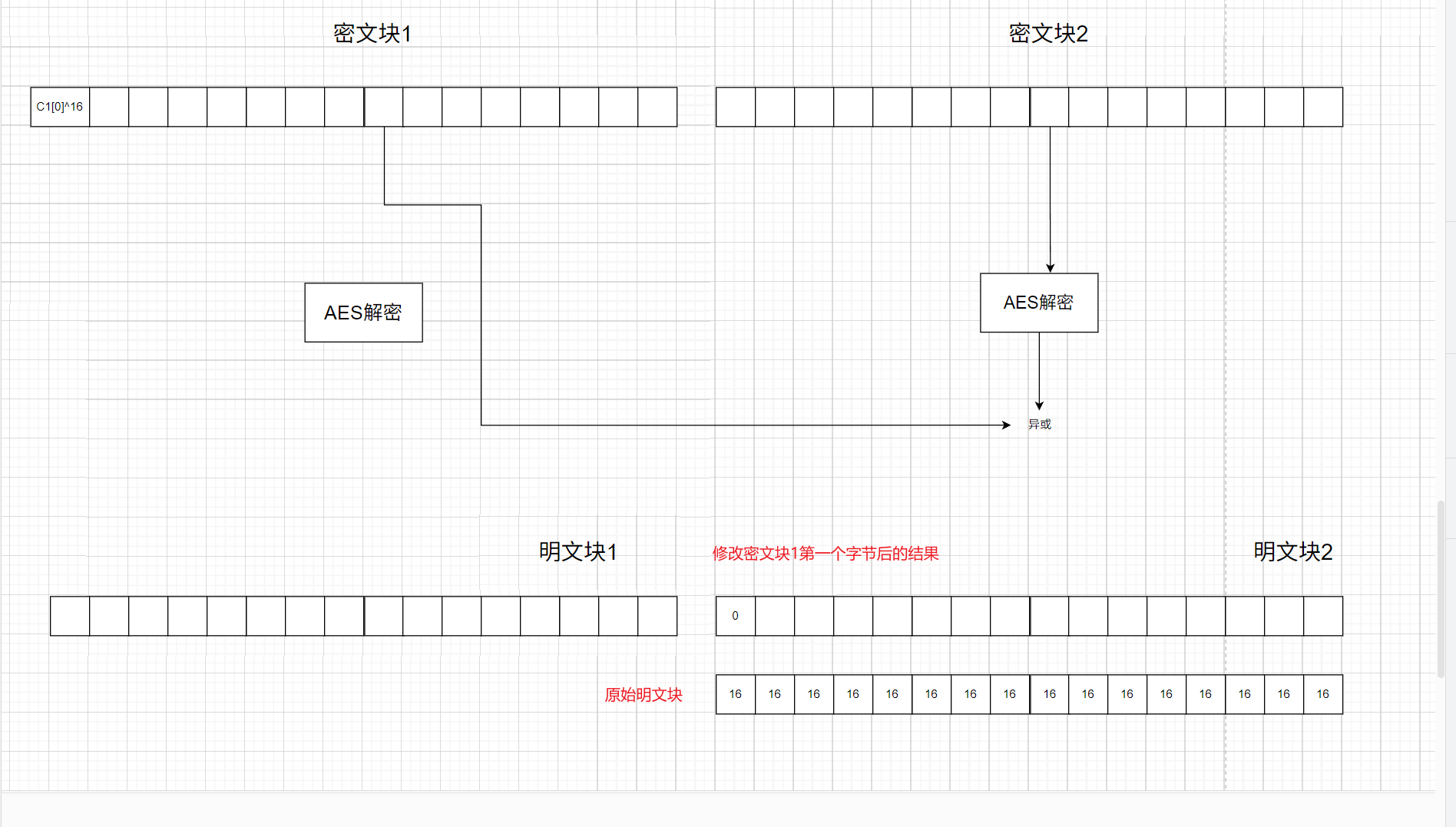
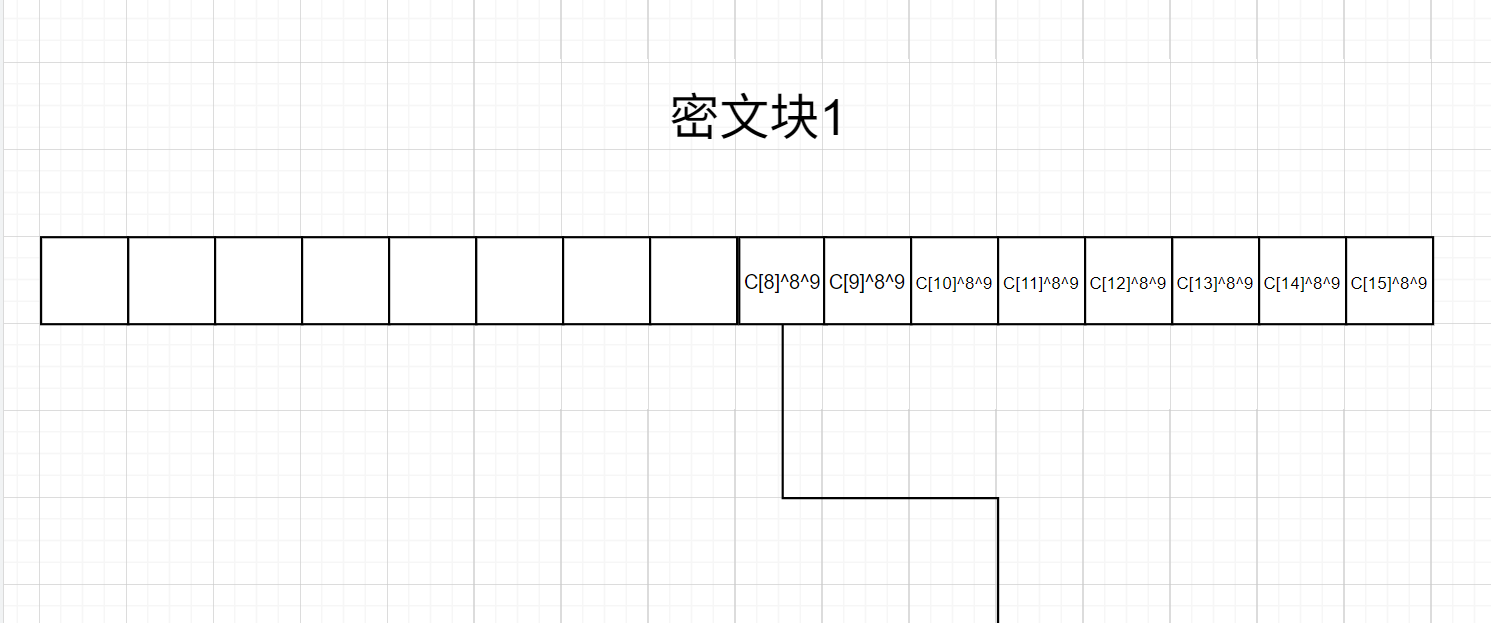
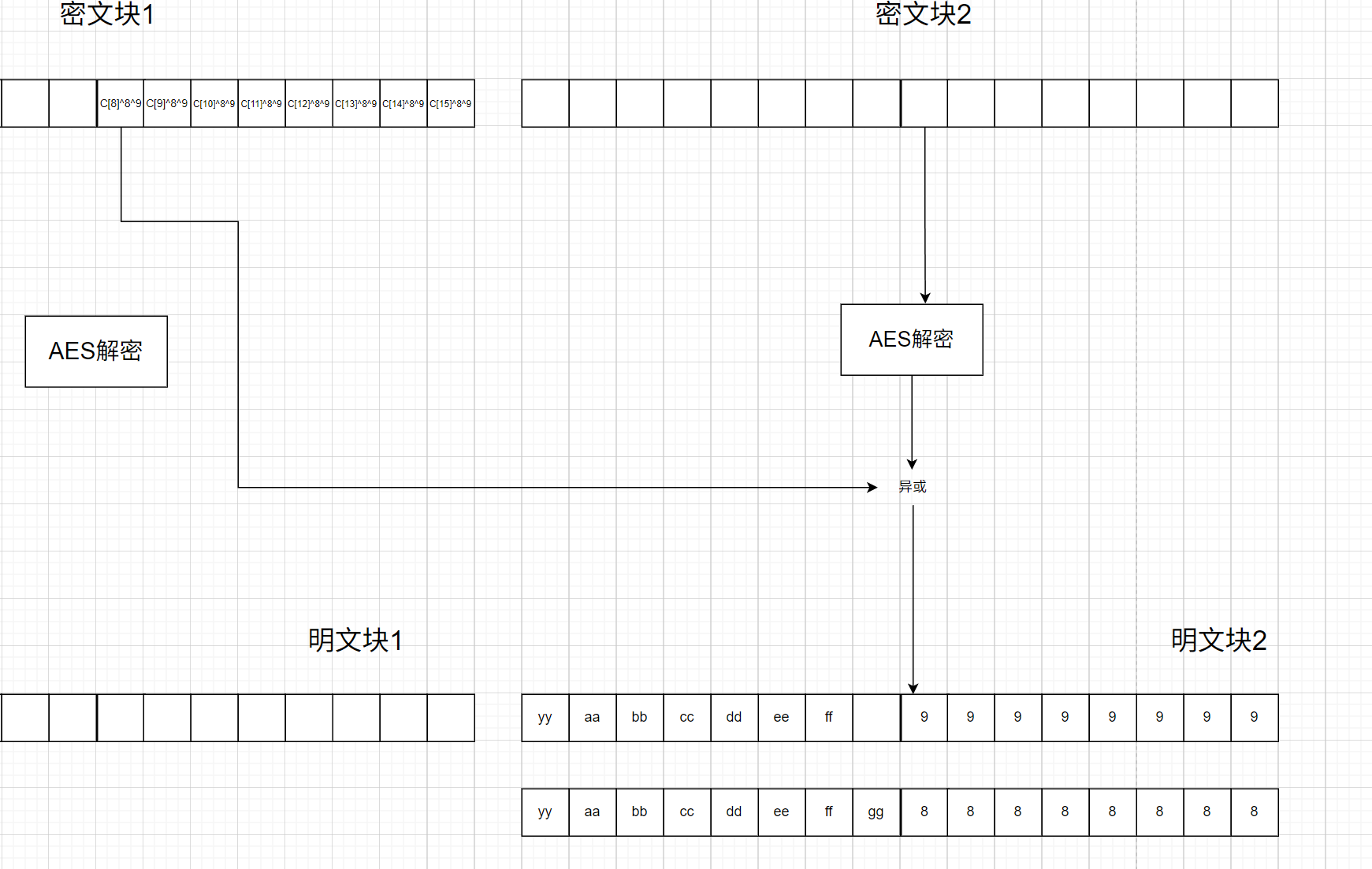
这时就会有以下两种情况（如下面俩张图）：

  • 当最后一块密文块填充的是16，此时解密后的数据pn′[0]=Pn[0]⊕16=16⊕16=0p'_n[0]=P_n[0]\oplus16=16\oplus16=0，在unpad的时候就会检查到有一个0字节，if set(padding) == {padbit}这句判断就会返回使得unpad返回NONE，从而使得用户收到false，此时我们就可以确定padding=16
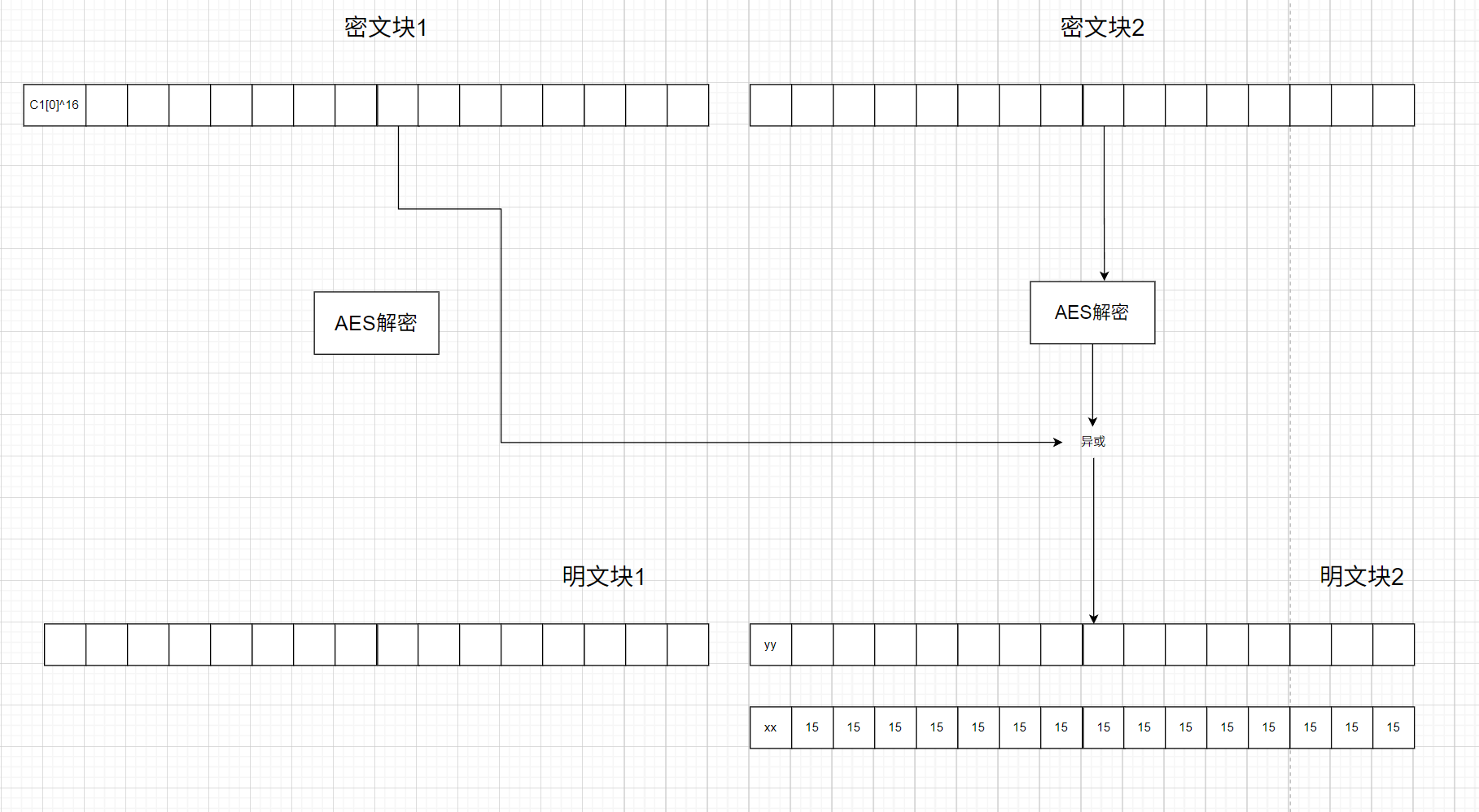
  • 当最后一块密文填充的不是16(以15位例子)，此时解密后的CnC_n的最后一个字节并不会被padding = s[-padbit:]这句提取，而是作为明文数据，所以返回的是True
  • 此时我们就可以根据Oracle says: False判断padding的长度

image-20250707220116917

image-20250707220827967

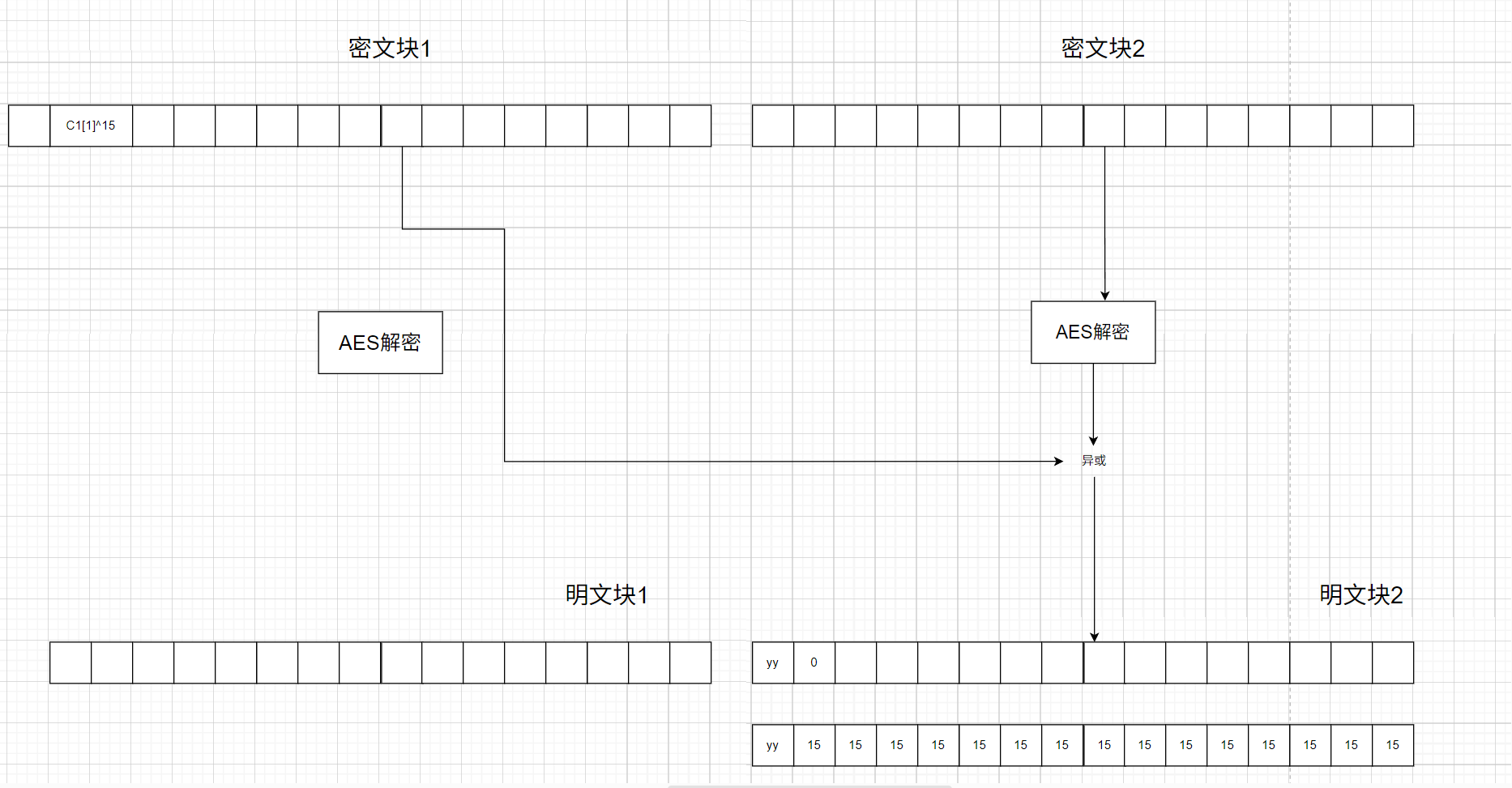
判断完padding不等于16后接下来就需要修改Cn−1′[1]=15C'_{n-1}[1]=15根据上式的推导，如果padding=15，此时就会返回False,如果padding不等于15那么就会返回True

之后就是重复这样的操作，直到返回false，这样就可以确定padding的值

image-20250707221747112

  • 编写的代码如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from pwn import *
import string
context.log_level='debug'
p =  remote("ip",9002)


p.recvuntil(b'Welcome to Padding oracle attack!!!\n')
c1 = p.recvline()[:-1].decode()
print(c1)
iv = c1[:32]
c2 = c1[32:]
print('密文:',c2)
print('初始化向量IV:',iv)
l = len(c2)
ll = l//32
#print(l)
print("密文可分组数:",l//32)
c_list = []
for i in range(ll):
    c_list.append(c2[i*32:i*32+32])
print("分组后的密文:",c_list)

def my_bytes(block): # 将密文块从16进制类型的转换为字节
    print(len(block))
    if len(block)==0:
        return b''
    else:
        return bytes.fromhex(block)



padding = 0
for i in range(16):
    block1 = my_bytes(c_list[-2])
    block2 = my_bytes(c_list[-1])
    payload = (block1[:i]+xor(block1[i],int(0x10-i).to_bytes(1,'big'))+block1[i+1:]+block2).hex().encode() # 修改block1[i]=block1[i]^(0x10-i),其他保持不变
    print(payload)
    p.sendlineafter(b'ct:',payload)
    p.recvuntil(b'Oracle says:  ')
    rec = p.recvline()[:-1].decode()
    print(rec)
    if rec=='False':  # 判断是否接收到False,只需要16~1即可,如果16~1都没返回false那么padding一定为0,所以我们就先初始化padding为0
        padding=0x10-i
        break
print("padding---->",padding)

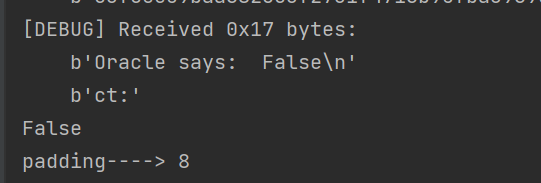
最后爆破出来的padding=8

image-20250707222710109

0x2爆破最后一块的非padding字符

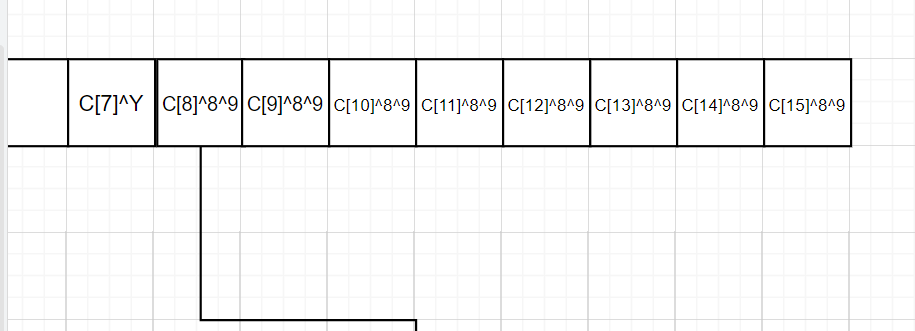
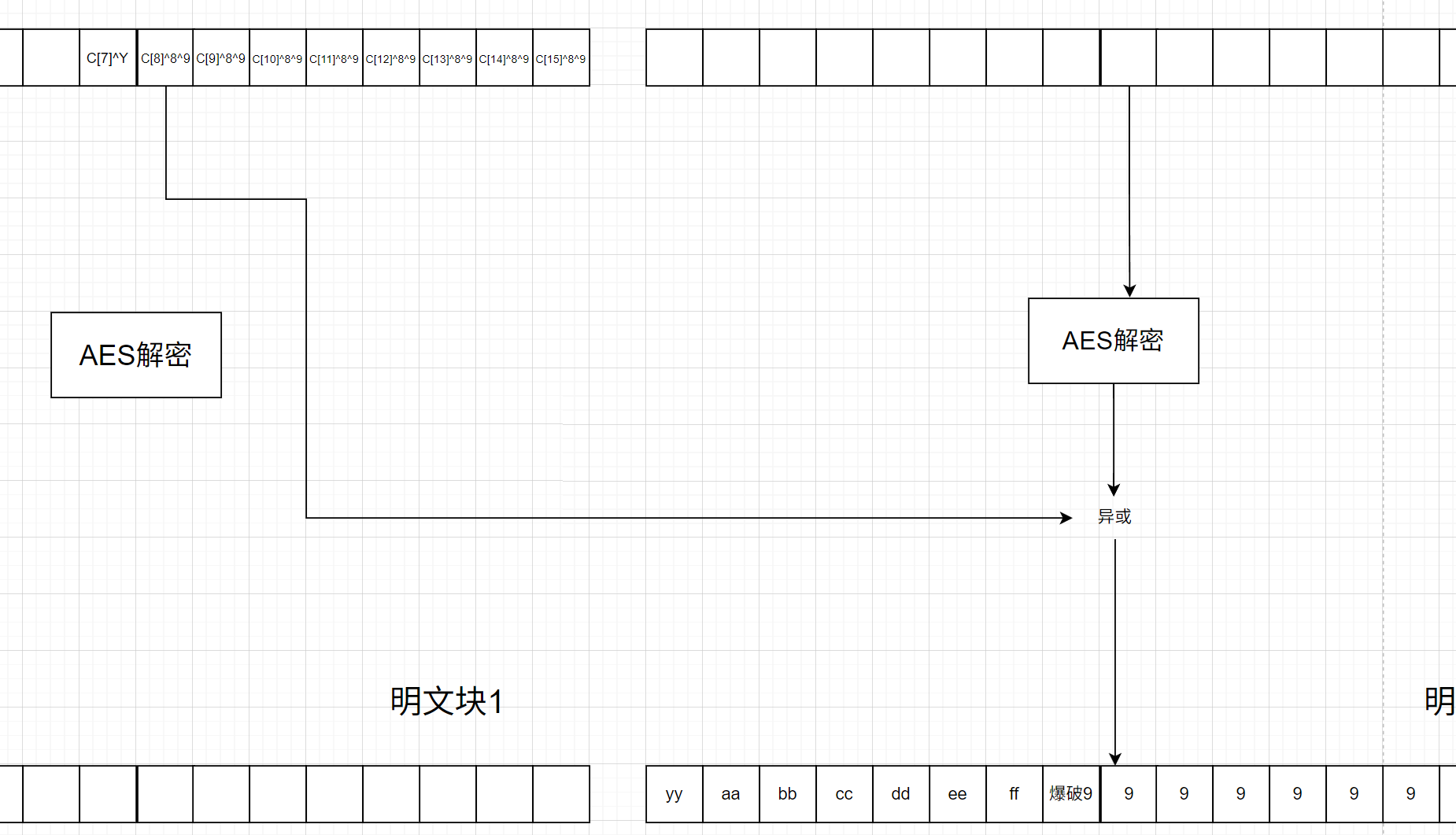
得到尾块填充长度后，攻击者就可以从右到左逐个破解尾块的非padding字符。设填充的长度为LL，由PKCS#7规范可以知道尾块明文块中最后L个字节数值全为L。攻击者先修改Cn−1C_{n-1}的最后L个字节。这里就以我们模拟的实验L=8来说明

\begin{align*} C'_{n-1}[j]&=C_{n-1}[j]\oplus P_n[j]\oplus(L+1),j=(16-L),...,15\\ &=C_{n-1}[j]\oplus8\oplus9 \end{align*}

image-20250707225751538

修改之后接收方执行了AES-CBC解密后就可以得到最后的L个字节为

\begin{align*} P'_n[j]&=X_n[j]\oplus C'_{n-1}[j]\\ &=(X_n[j]\oplus C_{n-1}[j])\oplus P_n[j]\oplus(L+1)\\ &=P_n[j]\oplus P_n[j]\oplus(L+1)\\ &=L+1 \end{align*}

image-20250707231105560

这样做就相当于强制解密后最后L个字节为L+1，所以此时unpad就会以为填充数L+1。此时攻击者尝试对Cn−1C_{n-1}倒数第L+1L+1个字节(就是要爆破的那个字节)执行如下操作：

\begin{align*} C'_{n-1}[15-L]=C_{n-1}[15-L]\oplus Y\\ \end{align*}

操作后这样在解密的后得到的明文有如下操作：

\begin{align*} P'_{n}[15-L] &= (X_n[15-L]\oplus C_{n-1}[15-L])\oplus Y\\ &=P_n[15-L]\oplus Y \end{align*}

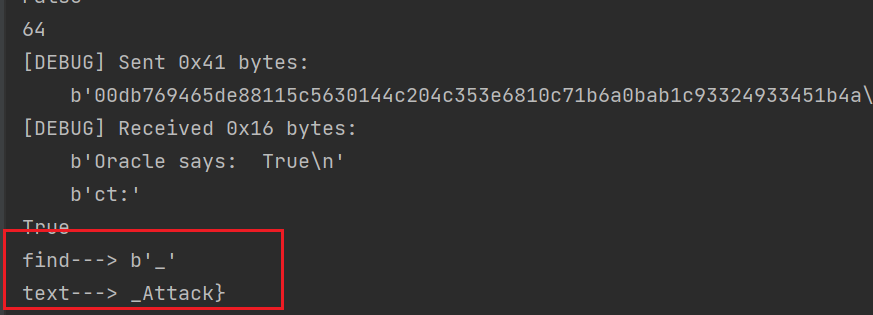
这里YY就是我们需要爆破的明文，而YY的取值为0~255，如果是可显字符串的话可以缩小范围。而在这一个区间内仅有一个YY使得Pn′[15−L]=L+1P'_n[15-L]=L+1，即倒数第L+1个字节也是L+1。这时整个区块以L+1个L+1结尾，是唯一unpad正确的情况，此时服务器就会发送True，当我们接收到True就意味着Pn′[15−L]=L+1P'_n[15-L]=L+1，这样就可以得到原始明文为：

Pn[15−L]=Pn′[15−L]⊕YP_n[15-L]=P_n'[15-L]\oplus Y

image-20250707232432258

image-20250707232515227

  • 当我们爆破到密文后，要爆破下一个密文：

image-20250707234123213

  • 这样我们就可以写出如下攻击脚本：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def pad(padding):
    return bytes([padding] * padding)

text = ''
for j in range(padding,16,1):
    padd = pad(padding) # 先计算原始padd
    padd2 = pad(j + 1)[:-1] # 再计算j+1的pad
    print(padd2)
    print(f"------------第{15-j}位爆破--------------")
    t = xor(block1[16-j:],text.encode()+padd) # 先计算C_i-1[j]^P_n[j]
    t2 = xor(t,padd2) # 最终计算得到C_i-1[j]^P_n[j]^(L+1)
    sleep(0.5)
    for i in range(0,256): # 注意这里的取值是0~255,而不是可显字符串,只能是0~255否则又可能爆破不出来
        payload = block1[:15-j]  # C_i-1[15-L]前面的数据不要动
        payload +=xor(block1[15-j],i.to_bytes(1,'big'))+t2 # 组合成第C_i-1密文块
        payload +=block2    #加上尾块
        payload = payload.hex().encode() # 转换为16进制字符形式,再转换为字节形式发送
        print(len(payload))
        p.sendlineafter(b'ct:',payload)
        p.recvuntil(b'Oracle says:  ')
        rec = p.recvline()[:-1].decode()
        print(rec)
        if rec=='True': # 判断是否能得到True的应答
            print("find--->",xor(i.to_bytes(1,'big'),j+1)) # 爆破到明文
            text = xor(i.to_bytes(1,'big'),j+1).decode() + text # 添加到text中
            print("text--->",text)
            sleep(1)
            break

最后一块密文块对应的明文数据我们就可以爆破出来了

image-20250707234419467

其他块密文

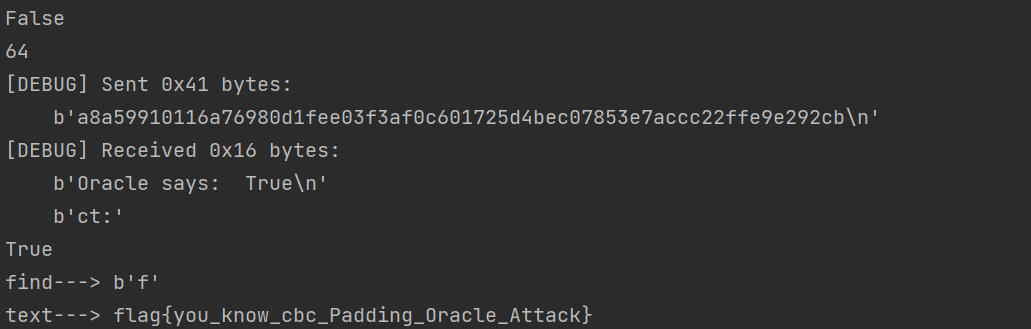
对于其他块密文攻击其攻击方法其实也是基于尾块的攻击，只不过这样的攻击其实padding都是从0开始，攻击过程基本一样。

image-20250707235331687

  • 最终的exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
from pwn import *
import string
context.log_level='debug'
p =  remote("ip",9002)


p.recvuntil(b'Welcome to Padding oracle attack!!!\n')
c1 = p.recvline()[:-1].decode()
print(c1)
iv = c1[:32]
c2 = c1[32:]
print('密文:',c2)
print('初始化向量IV:',iv)
l = len(c2)
ll = l//32
#print(l)
print("密文可分组数:",l//32)
c_list = []
for i in range(ll):
    c_list.append(c2[i*32:i*32+32])
print("分组后的密文:",c_list)

def my_bytes(block): # 将密文块从16进制类型的转换为字节
    print(len(block))
    if len(block)==0:
        return b''
    else:
        return bytes.fromhex(block)


# ---------爆破padding--------------
padding = 0
for i in range(16):
    block1 = my_bytes(c_list[-2])
    block2 = my_bytes(c_list[-1])
    payload = (block1[:i]+xor(block1[i],int(0x10-i).to_bytes(1,'big'))+block1[i+1:]+block2).hex().encode() # 修改block1[i]=block1[i]^(0x10-i),其他保持不变
    print(payload)
    p.sendlineafter(b'ct:',payload)
    p.recvuntil(b'Oracle says:  ')
    rec = p.recvline()[:-1].decode()
    print(rec)
    if rec=='False':  # 判断是否接收到False,只需要16~1即可,如果16~1都没返回false那么padding一定为0,所以我们就先初始化padding为0
        padding=0x10-i
        break
print("padding---->",padding)

def pad(padding):
    return bytes([padding] * padding)

# ---------爆破尾块密文数据--------------
text = ''
for j in range(padding,16,1):
    padd = pad(padding) # 先计算原始padd
    padd2 = pad(j + 1)[:-1] # 再计算j+1的pad
    print(padd2)
    print(f"------------第{15-j}位爆破--------------")
    t = xor(block1[16-j:],text.encode()+padd) # 先计算C_i-1[j]^P_n[j]
    t2 = xor(t,padd2) # 最终计算得到C_i-1[j]^P_n[j]^(L+1)
    sleep(0.5)
    for i in range(0,256):
        payload = block1[:15-j]  # C_i-1[15-L]前面的数据不要动
        payload +=xor(block1[15-j],i.to_bytes(1,'big'))+t2 # 组合成第C_i-1密文块
        payload +=block2    #加上尾块
        payload = payload.hex().encode() # 转换为16进制字符形式,再转换为字节形式发送
        print(len(payload))
        p.sendlineafter(b'ct:',payload)
        p.recvuntil(b'Oracle says:  ')
        rec = p.recvline()[:-1].decode()
        print(rec)
        if rec=='True': # 判断是否能得到True的应答
            print("find--->",xor(i.to_bytes(1,'big'),j+1)) # 爆破到明文
            text = xor(i.to_bytes(1,'big'),j+1).decode() + text # 添加到text中
            print("text--->",text)
            sleep(1)
            break

# ---------非尾块密文数据--------------
text1 = ''
#爆破非尾块的第一个字节需要特殊处理
for i in range(0,256):
    block1 = my_bytes(c_list[0]) # 取密文块0
    block2 = my_bytes(c_list[1]) # 取密文块1
    payload = block1[:15]
    payload += xor(block1[15], i.to_bytes(1,'big'))
    payload += block2
    payload = payload.hex().encode()  # 转换为16进制字符形式,再转换为字节形式发送
    print(len(payload))
    p.sendlineafter(b'ct:', payload)
    p.recvuntil(b'Oracle says:  ')
    rec = p.recvline()[:-1].decode()
    print(rec)
    if rec == 'True':  # 判断是否能得到True的应答
        print("find--->", xor(i.to_bytes(1,'big'), 1))  # 爆破到明文
        text = xor(i.to_bytes(1,'big'), 1).decode() + text  # 这里应该需要修改为异或1
        print("text--->", text)
        text1 = xor(i.to_bytes(1,'big'), 1).decode() + text1
        sleep(1)
        break

for j in range(1,16,1):
    block1 = my_bytes(c_list[0]) # 取密文块0
    block2 = my_bytes(c_list[1]) # 取密文块1
    padd2 = pad(j + 1)[:-1] # 再计算j+1的pad
    print(padd2)
    print(f"------------第{15-j}位爆破--------------")
    print("text1--->",text1)
    t = xor(block1[16-j:],text1.encode()) # 先计算C_i-1[j]^P_n[j], 相比于前面这里去掉了padd
    t2 = xor(t,padd2) # 最终计算得到C_i-1[j]^P_n[j]^(L+1)
    sleep(0.5)
    for i in range(0,256):
        payload = block1[:15-j]  # C_i-1[15-L]前面的数据不要动
        payload +=xor(block1[15-j],i.to_bytes(1,'big')) + t2 # 组合成第C_i-1密文块
        payload +=block2    #加上尾块
        payload = payload.hex().encode() # 转换为16进制字符形式,再转换为字节形式发送
        print(len(payload))
        p.sendlineafter(b'ct:',payload)
        p.recvuntil(b'Oracle says:  ')
        rec = p.recvline()[:-1].decode()
        print(rec)
        if rec=='True': # 判断是否能得到True的应答
            print("find--->",xor(i.to_bytes(1,'big'),j+1)) # 爆破到明文
            text = xor(i.to_bytes(1,'big'),j+1).decode() + text # 添加到text中
            print("text--->",text)
            text1 = xor(i.to_bytes(1,'big'),j+1).decode() + text1
            sleep(1)
            break


# ---------爆破第一块密文数据--------------
# 接下来就是IV和密文块0了
text1 = ''
block1 = my_bytes(iv) # 取初始向量IV
block2 = my_bytes(c_list[0]) # 取密文块0
for i in range(0,256):
    payload = block1[:15]
    payload += xor(block1[15], i.to_bytes(1,'big'))
    payload += block2
    payload = payload.hex().encode()  # 转换为16进制字符形式,再转换为字节形式发送
    print(len(payload))
    p.sendlineafter(b'ct:', payload)
    p.recvuntil(b'Oracle says:  ')
    rec = p.recvline()[:-1].decode()
    print(rec)
    if rec == 'True':  # 判断是否能得到True的应答
        print("find--->", xor(i.to_bytes(1,'big'), 1))  # 爆破到明文
        text = xor(i.to_bytes(1,'big'), 1).decode() + text  # 这里应该需要修改为异或1
        print("text--->", text)
        text1 = xor(i.to_bytes(1,'big'), 1).decode() + text1
        sleep(1)
        break

for j in range(1,16,1):
    padd2 = pad(j + 1)[:-1] # 再计算j+1的pad
    print(padd2)
    print(f"------------第{15-j}位爆破--------------")
    print("text1--->",text1)
    t = xor(block1[16-j:],text1.encode()) # 先计算C_i-1[j]^P_n[j], 相比于前面这里去掉了padd
    t2 = xor(t,padd2) # 最终计算得到C_i-1[j]^P_n[j]^(L+1)
    sleep(0.5)
    for i in range(0,256):
        payload = block1[:15-j]  # C_i-1[15-L]前面的数据不要动
        payload +=xor(block1[15-j],i.to_bytes(1,'big')) + t2 # 组合成第C_i-1密文块
        payload +=block2    #加上尾块
        payload = payload.hex().encode() # 转换为16进制字符形式,再转换为字节形式发送
        print(len(payload))
        p.sendlineafter(b'ct:',payload)
        p.recvuntil(b'Oracle says:  ')
        rec = p.recvline()[:-1].decode()
        print(rec)
        if rec=='True': # 判断是否能得到True的应答
            print("find--->",xor(i.to_bytes(1,'big'),j+1)) # 爆破到明文
            text = xor(i.to_bytes(1,'big'),j+1).decode() + text # 添加到text中
            print("text--->",text)
            text1 = xor(i.to_bytes(1,'big'),j+1).decode() + text1
            sleep(1)
            break

image-20250708005045106

板子

CBC-R伪造明文

字节翻转攻击

密文填充攻击(Padding Oracle)论文

CTR模式

CFB模式

OFB模式

GCM模式