基础知识

简单了解几个数论的概念会更好的理解离散对数问题。

欧拉定理：对于任意的$a,m$只要$gcd(a,m)=1$，那么就有$a^{\phi(n)}\equiv 1 ~mod(~m)$

模指数的阶：与m互质的整数a，我们记满足$a^{n}\equiv1~(mod~m)$的最小正整数n为a模m的阶

推论：对于任意的$a,m$只要$gcd(a,m)=1$，$n$为a模m的阶，那么就有$n|\phi(n)$

原根：若存在与m互质的整数$g$，并且$g$模$m$的阶为$phi(n)$，那么我们称模m有原根，并称$g$为模$m$的一个原根。实际上就是阶等于$\phi(n)$的时候原根存在

离散对数

了解了指数、原根和阶的概念，其实还可以发现一个规律：设a模m的阶为$n$，那么根据同余的指数运算性质可以发现，$a^x\equiv b~mod(~m)$，这个指数运算得到的模结果其实发生循环，b的取值范围其实就为$b\in{a^0~mod~(m),…,a^{n-1}~mod~(m)}$，模的指数运算的结果存在周期性，其周期为$n$。
这里的$a$，在抽象代数的群论中有一个称呼即$生成元$，也称为本原元。设G是一个群（可以理解为一个集合，该集合里面的元素可以满足特定的运算，例如集合：${a^0~mod~(m),…,a^{n-1}~mod~(m)}$），如果集合中存在一个元素$a\in G$，通过对g进行重复的群运算，可以得到G中的每个元素，那么g就被称为G的生成元。
由上面的指数、原根和阶的定义，就可以引入一个离散对数的问题，已知模的幂y、底数g、模数p，要我们求出指数x使得下面式子成立：
- 求解这个问题通用解法只能是从0~n-1（n为g模p下的阶）遍历，判断是否$g^k\equiv y~(mod~p)$
- 当模数p比较小的时候，并且n也较小的时候，求得x算是比较容易的
- 但是当模数p很大、下式的阶n也很大或者下式存在原根，那要遍历的范围就相当的大（这就导致了在有限的时间无法求得x，这就是著名的离散对数问题）

$$
y\equiv g^x~(mod~p)\Leftrightarrow x=log_g(y)~mod~(p)
$$

离散对数和大整数分解问题类似，都是不能够在有限的时间内得到答案。基于大整数分解问题得到了著名的RSA加密算法，而基于离散对数问题密码学家也提出了对应的加密算法如Diffie-Hellman密钥交换协议(简称DH密钥交换协议)、ElGamal加密算法、DSA数字签名算法、ECDLP椭圆曲线上的离散对数问题。

求解离散对数的方法

暴力破解法

暴力破解法是最一般的求解离散对数的算法，就是1遍历到n-1，计算每个模指数的值，直到找到一个指数使其满足$y \equiv g^x$才退出循环（由于计算阶还需要时间，这里一般n都是直接用模数的欧拉函数）

def discrete_log(y,g,p):
    """
    y : 模的幂
    g : 底数
    p : 模数
    """
    n = p-1 # 阶数,当有原根的时候阶数就是p-1,所以一般都取p-1
    for i in range(1,n):
        t = pow(g,i,p)
        if t==y:
            print(f"找到目标指数x={i}")
            break
    return i

BSGS算法

BSGS算法本质上也是暴力破解，但是BSGS是经过算法优化后再进行遍历操作，时间复杂度会低一些，但是该算法的思想有用上meet-in-the-middle即中间相遇攻击的思想。其推导过程如下：
- 对于下面的式子，我们可以得到$yg^{b}\equiv g^{Ka}~mod(~p)$，其中$q\in{1,2,…,K}$，$a\in{1,2,3,…,\left\lceil \frac{p}{K}\right\rceil}$，这样$Ka-b\in{0,1,…,p-1}$，同样可以达到从0~p-1的遍历效果。
- 接下来先选取一个K（K取$\sqrt{p}$时间复杂度达到最小），遍历计算$y*g^{b}~mod(~p)$的结果，并且存储计算结果及其对应的b。
- 存储得到b后，再遍历a的取值计算$g^{Ka}~mod(~p)$，并判断计算结果与前面计算的$yg^{b}$的其中一个相等（这里就会出现查找的步骤，使用哈希表查找应该是最快的），如果找到相等的数，那么也就找到了这个式子的指数x
- 最后计算$x=Ka-b$，即可得到结果。
- 注意：BSGS有俩中构造方式一种就是Ka-b还有一种是Ka+b这俩中形式，但是貌似Ka+b是论文原始的构造方法

$$
y \equiv g^x~(mod~p)\
\iff y \equiv g^{Ka-b} ~(mod~p)\
\iff y \equiv g^{Ka}g^{-b}~mod(~p)\
\iff yg^{b} \equiv g^{Ka}~mod(~p)
$$

下面是BSGS的伪代码：

Input: g,y,p
output: x

K := ⌈√p⌉
value_table := empty_hash_map
value := y mod p


for q from 0 to K+1 do
	value_table[value] <- q
	value = value * g mod p
	
ak = pow(a,k,p) // 先计算 a^k mod p,避免循环的时候重复计算
search_value = 1
for a from 1 to K+1 do
	search_value <- pow(ka,a,p) 
	if search_value in value_table then:
		j <- value_table[search_value]
		return x <- a * k - j
	end if
	
return "no solution"

Python代码如下：

def bsgs(p,g,y):
    if math.gcd(g,p)!=1:
        return None

    K = int(math.sqrt(p))+1
    value_table = dict()
    value = y % p

    for i in range(K):
        value_table[value] = i
        value = (value * g) % p

    gk = pow(g,K,p) # g ^ K

    for a in range(1,K):
        t = pow(gk,a,p)
        if t in value_table:
            b = value_table[t]
            find = K * a - b
            return find

    return None

Pohlig-Hellman算法

Pohlig-Hellman算法是经典用于加速离散对数求解的算法，只适用于一种模数比较特殊的情况即模数p要满足b-光滑数，该算法的本质其实就是将大整数下的离散对数问题，转换为若干个小模数下的离散对数问题，并且使用中国剩余定理求解

B-Smooth number(B光滑数)：一个正整数它的所有质因数都不大于B，则该正整数就被称为B光滑数，而这个数B并不确定，但是它通常取决于算法的需要和计算资源。

Pollard λ算法

Pollard’s Rho算法

sagemath相关函数

sage中discrete_log就是利用Pohlig-Hellman算法和BSGS算法实现的。如果使用sage，只需要调用discrete_log这个函数即可。
详细说明一下discrete_log的参数，记要求的相关高次同余式如下：$base ^x\equiv a~mod(~n)$
- 参数a：就是模幂的结果
- 参数base：作为底数
- 参数ord：群的阶，如果知道群的阶就可以填入，可以加快计算
- 参数bounds：指数的搜索范围，即在给定区间内寻找离散对数，可以加快搜索，格式(lower_bound,upper_bound)例如：(100,1000)
- 参数operation：群操作类型，默认为乘法
- 参数identity：单位元，通常是函数内部自动处理，若自定义群结构就像ECC那样，可以手动设置
- 参数inverse：取逆函数，默认为None，也可以传一个函数用于计算逆元
- 参数op：自定义操作函数可选
- 参数algorithm：默认是bsgs也就是默认使用bsgs算法求离散对数，还可以有rho选项（使用pollard_rho算法求离散对数），lambda选项(λ 算法Pollard lambda，又叫“kangaroo”方法)，automatic选项Sage自动判断哪种算法更优

discrete_log(
    a,
    base,
    ord=None,
    bounds=None,
    operation='*',
    identity=None,
    inverse=None,
    op=None,
    algorithm='bsgs',
)

discrete_log的使用：

b = Mod(2,37) 		# 先使用Mod(n,m)创建一个底数为n,模数为m的对象,返回的是整数n,n作为Z/mZ中的元素
a = b^20		 	# 计算模的幂
discrete_log(a,b)	
# 20

discrete_log(a,b,bounds=(10,100)) # 限定指数x的范围,求解离散对数
# 20
discrete_log(a,b,bounds=(30,40))
# 32

discrete_log源码如下：

def discrete_log(a, base, ord=None, bounds=None, operation='*', identity=None, inverse=None, op=None, algorithm='bsgs'):
    from operator import mul, add, pow
    power = mul if operation in addition_names else pow
    mult = add if operation in addition_names else mul
    if op:
        mult = op
        power = lambda x, y: multiple(x, y, operation=operation, identity=identity, inverse=inverse, op=op)
    if bounds:
        lb, ub = map(integer_ring.ZZ, bounds)
    if (op is None or identity is None or inverse is None or ord is None) and operation not in addition_names + multiplication_names:
        raise ValueError("ord, op, identity, and inverse must all be specified for this operation")
    if ord is None:
        if operation in multiplication_names:
            try:
                ord = base.multiplicative_order()
            except Exception:
                ord = base.order()
        else:
            try:
                ord = base.additive_order()
            except Exception:
                ord = base.order()
    else:
        ord = integer_ring.ZZ(ord)
    try:
        from sage.rings.infinity import Infinity
        if ord == +Infinity:
            return bsgs(base, a, bounds, identity=identity, inverse=inverse, op=op, operation=operation)
        if base == power(base, 0) and a != base:
            raise ValueError
        f = ord.factor()
        l = [0] * len(f)
        mods = []
        running_mod = 1
        offset = 0
        if bounds:
            a = mult(a, power(base, -lb))
            offset = lb
            bound = ub - lb
        i = -1  # this corrects a bug in which the loop is never entered and i never gets assigned a value
        for i, (pi, ri) in enumerate(f):
            gamma = power(base, ord // pi)
            # pohlig-hellman doesn't work with an incorrect order, and the user might have provided a bad parameter
            while gamma == power(gamma, 0) and ri > 0:  # identity might be None
                ord //= pi
                ri -= 1
                gamma = power(base, ord // pi)
            if not bounds:
                bound = ord - 1
            running_bound = min(bound, pi**ri - 1)
            j = -1
            for j in range(ri):
                temp_bound = min(running_bound, pi - 1)
                h = power(mult(a, power(base, -l[i])), ord // pi**(j + 1))
                if algorithm == 'bsgs':
                    c = bsgs(gamma, h, (0, temp_bound), inverse=inverse, identity=identity, op=op, operation=operation)
                elif algorithm == 'rho':
                    c = discrete_log_rho(h, gamma, ord=pi, inverse=inverse, identity=identity, op=op, operation=operation)
                elif algorithm == 'lambda':
                    c = discrete_log_lambda(h, gamma, (0, temp_bound), inverse=inverse, identity=identity, op=op, operation=operation)
                l[i] += c * (pi**j)
                running_bound //= pi
                running_mod *= pi
                if running_mod > bound:
                    break
            mods.append(pi ** (j+1))
            if running_mod > bound:
                break  # we have log%running_mod. if we know that log<running_mod, then we have the value of log.
        l = l[:i + 1]
        from sage.arith.misc import CRT_list
        return (CRT_list(l, mods) + offset) % ord
    except ValueError:
        raise ValueError("no discrete log of %s found to base %s" % (a, base))

离散对数加密

ElGamal加密算法

ElGamal加密算法是一种基于离散对数难题的公钥加密算法，由Taher ElGamal于1985年提出。是非对称加密算法。

ElGamal提出了一个基于$(Z^{}_p,·)$(即模数p为素数)上离散对数问题的公钥密码体制.设p是一个素数，使得$(Z^{}_p，·)$上的离散对数问题是最难处理的

ElGamal加密算法如下：
- 首先选取一个大素数p，令生成元为g
- 选取明文空间$0<m<p$范围中的整数
- 而密文也是$0<c_1,c_2<p$范围内的整数。
- 选取密钥K有四个元素，其中三个元素作为公钥，一个元素作为私钥，密钥满足关系$K\in{(p,g,a,h)|h\equiv g^a mod~p}$，其中$(p,g,h)$是公钥，$a$是私钥
- 加密函数如下：
  - $c_1=g^k~mod~p$
  - $c_2=m*h^k~mod~p$
  - $e_K(m,k)=(c_1,c_2)$
- 解密函数：$d_K(c_1,c_2) = c_2(c_1^{a})^{-1}~mod~p$
解密推导过程：$c_2(c_1^{a})^{-1}=m*h^{k}((g^k)^a)^{-1} = mh^{k}((g^a)^k)^{-1}=mh^k(h^k)^{-1}=m$

注：ElGamal密码体制中，加密运算是随机的，因为密文既依赖于明文m，也依赖于加密者所选择的随机数k，所以对于同一个明文，会有p-1个可能的密文，这个加密体制其实是概率加密

Diffie-Hellman密钥交换协议

Diffie-Hellman密钥交换协议简称DH密钥交换
DH密钥交换也是基于离散对数问题的。设$p$是一个素数，使得$(Z^*_p,·)$上的离散对数问题是难处理的，另g为生成元
密钥交换者A：
- 随机选择一个整数$x_A,0≤x_A≤p-2$
- 计算$y_A=g^{x_A}~mod~p$，并且将$y_A$发送给B
密钥交换者B：
- 随机选择一个整数$x_B,0≤x_B≤p-2$
- 计算$y_B=g^{x_B}~mod~p$，并且将$y_B$发送给A
双方得到对方发送的值后进行计算，交换者A计算：$k_A=y_B^{x_A}~mod~p$；交换者B计算$k_B=y_A^{x_B}~mod~p$
这样就可以得到：$k_A=y_B^{x_A}=(g^{x_B})^{x_A}=(g^{x_A})^{x_B}=y_A^{x_B}=k_B$

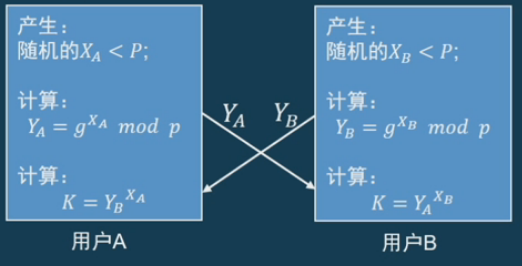
由于离散对数的困难性问题，这就导致了攻击者知道$Y_A$或者$Y_B$的其中一个得到$K$是非常困难的。
并且这里又引出一个新的困难性问题CDH问题：给定$g^{x_A}$，$g^{x_B}$，计算$g^{x_Ax_B}$也是很困难的。

DLP离散对数