一些算法概念

判定问题：只回答是或者否的问题，也就是算法的返回值只有True或者False

随机算法：使用了随机数的算法

判定问题偏是(Yes-biased)Monte-Carlo算法：算法给出是的回答总是正确的，给出否的回答也许不正确。如果对应该为是的输入至多以$\varepsilon$的概率给出否的答案则说该算法具有错误概率$\varepsilon$

判定问题偏否(No-biased)Monte-Carlo算法：算法给出否的回答总是正确的，给出是的回答也许不正确。如果对应该为否的输入至多以$\varepsilon$的概率给出是的答案则说该算法具有错误概率$\varepsilon$

素性检验介绍

  • 在公钥密码学中经常都是要生成一个大素数，而大素数是没办法直接生成的，需要随机生成一个大数，在判断该数是否为素数。

  • 由于生成的是一个大数，程序没办法遍历2到该数的平方根发现该数是否有因子，这种方法对大数并不高效，所以就需要设计一个算法判断一个大数是否为素数。判断一个数是否为素数这个行为就是素性检验

  • 具体介绍一下生成随机素数的一般方法：

    • 生成随机整数n
    • 判断n是否为素数，有两种判断方法，即确定性算法、随机算法：
      1. 确定性算法：以概率1确定n是否为素数，2002年三位印度计算机科学家发现了第一个多项式时间的算法，称为AKS素性检测，计算复杂度为$O(log^{12}(n))$
      2. 随机算法：如果n通过某些素数判定准则，则n可能为素数，如果不通过则n肯定为合数。如：Fermat素性检测、Miller-Rabin素性检测、Solovay-Strassen素性检测、Lucas素性检测

  • 这里先对成功概率进行分析：在1~N之间随机选取一个数，其为素数的概率约为$\frac{1}{lnN}$，这个其实就是素数的密度。

  • 在RSA加密算法中，大素数p、q选取为512bit的素数，其成功概率为$\frac{1}{ln2^{512}}\approx\frac{1}{355}$，即可以在随机选取的355个数中以高概率找到一个素数的。

Fermat素性检验

  • Fermat素性检验是一个判定问题偏否(No-biased)Monte-Carlo算法，该检验算法是随机算法，目前该素性检验方法已经过时了。

  • 应用：PGP（邮件加密软件）使用Fermat素性检测算法，在PGP中，通过测试的数为Carmichael数的概率小于$\frac{1}{10^{50}}$

  • Fermat素性检验算法原理其实就是费马小定理：若p是素数，则$a^{p-1}=a~mod(~p)$，或者$a^{p-1}\equiv1~mod(~p)$。

  • 算法的具体过程：

  • 该算法的代码实现：

1
2
def Fermat_test():
  • Fermat素性检验存在的缺陷：存在这样的合数n，使得$0<a<n,gcd(a,n)=1,a^{n-1}\equiv1~mod(~n)$，这样的合数称为Carmichael数，如561是一个Carmichael数。

Miller-Rabin素性检验

  • Miller-Rabin算法对于合数问题是一个偏是的Monte Carlo算法。

  • Miller-Rabin素性检验，也被称为强伪素数检验，是对Fermat检测的改进。该算法目前为止很常用。

  • Miller-Rabin素性检验的原理：

    • 当n为素数的时候，对于二次同余方程$x^{2}\equiv 1~(mod~n)\Leftrightarrow x\equiv \pm1~mod(~n)$
    • 设$n-1=2^{k}m$，其中m是奇数，若$(a,n)=1$，则可以由费马小定理得到：
      • $a^{n-1}=a^{2^{k}m}\equiv1~(mod~n)\Leftrightarrow a^{2^{k-1}m}\equiv \pm1~(mod~n)$
      • 如果$a^{2^{k-1}m}\equiv1~(mod~n)\Leftrightarrow a^{2^{k-2}m}\equiv \pm1~(mod~n)$
      • 如果$a^{2^{k-2}m}\equiv1~(mod~n)\Leftrightarrow a^{2^{k-3}m}\equiv \pm1~(mod~n)$
      • …
      • 如果$a^{2m}\equiv1~(mod~n)\Leftrightarrow a^{m}\equiv \pm1~(mod~n)$
    • 这样对于序列$a^{m},a^{2m},…,a^{2^{k-1}m},a^{2^{k}m}~(mod~n)$就会得到这样的一个序列：$(1,1,…,1)$或者$(,,…,*,-1,1,…,1)$。
    • 对于一个随机数，按照上述方法计算，如果p是素数，就会得到序列$(1,1,…,1)$或者$(,,…,*,-1,1,…,1)$，如果p不是素数，就不会得到该序列

  • 算法具体过程：

    • 第一步：先把$n-1$写成$2^km$的形式，其中m是一个奇数

    • 第二步：使用随机数生成器，生成一个整数$a\in[1,n-1]$

    • 第三步：

      • $b\leftarrow a^m~(mod~n)$。这里直接先从$a^{m}$开始检查
      • $if~b\equiv 1~(mod~n)$，return "n is prime"。先检查形式是否为(1,1,...,1)。

    • 第四步：

      • for i<- 0 to k-1

      • do：

        $if~b\equiv-1(mod~n)$，return "n is prime"此时判断形式是否为(*,...,*,-1,1,...)）

        $else~b\leftarrow b^2 ~(mod~n)$

      • return "n is composite"

  • 代码实现如下：

1
def Miller_Rabin_test():
  • 错误概率分析：
    • 如果黎曼猜想为真，Miller-Rabin素性检验可以转为确定性算法。当目前算法的确定性与否还不知道。
    • 如果n是奇合数，则在${1,…,n-1}$范围内至多有$\frac{n-1}{4}$个a能让n通过Miller-Rabin检测
    • 这说明奇合数只有至多$\frac{1}{4}$的概率通过一次Miller-Rabin检测，则奇合数通过k次的Miller-Rabin检测的概率至多为$\frac{1}{4^{k}}$（但是这并不是错误概率）
    • 错误概率：n通过了素性检测，但n是合数的概率。（该问题是一个条件概率的问题）。先定义两个随机变量也就是，定义a: 一个特定长度的随机奇整数n是合数，定义b: 算法连续回答了m次"n是一个素数"，则求错误概率其实就是求条件概率$P(a\mid b)$，也就是当事件b发生时，事件a发生的概率。
      • 可以很容易知道奇整数n为素数的概率：$P(\bar{a})\approx \frac{2}{ln~n}$，因为素数在整数的分布为$\frac{1}{ln~n}$，而在奇整数的概率就翻倍了。这样就可以得到$P(a)\approx 1 - \frac{2}{ln~n}$
      • 还可以知道在已知n为奇素数条件下,事件b是必然发生即：$P(b\mid \bar{a})= 1$，由条件概率$P(b\mid\bar{a})=\frac{P(\bar{a}b)}{P(\bar{a})}$
      • 由上面可以知道在已知n为奇合数条件下,算法m次回答"n是一个素数"的概率：$P(b\mid a)≤\frac{1}{4^{m}}$由条件概率可以知道，$P(b\mid a)=\frac{P(ab)}{P(a)}$
      • 那么由条件概率和全概率的公式就可以得到：$P(a\mid b)=\frac{P(ab)}{P(b)}=\frac{P(b\mid a)P(a)}{P(b\mid a)P(a)+P(b\mid \bar{a})P(\bar{a})}≤\frac{\frac{1}{4^m}(1-\frac{2}{ln~n})}{\frac{1}{4^{m}}(1-\frac{2}{ln~n})+\frac{2}{ln~n}}=\frac{ln~n-2}{ln~n-2+2^{2m+1}}$
    • 从错误概率的推导可以看出，随着检测次数的增加，错误概率是逐渐降低的。
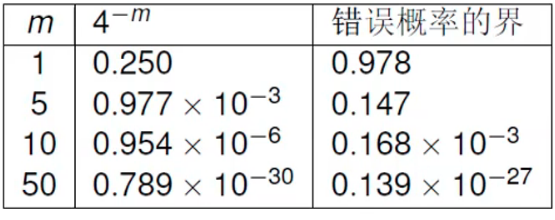
  • 下图给出错误概率的一张表：

image-20250822004159274

Solovay-Strassen素性检验

Lucas素性检验

Python-Crypto.Util.number源码

  • 对于Python中的Crypto.Util.number应该都不陌生，经常都在用，这里主要分析三个函数的源码，即getPrime、isPrime、_rabinMillerTest这三个函数，其中getPrime中有使用isPrime函数，而isPrime中有使用的就是_rabinMillerTest函数作为素性检测算法
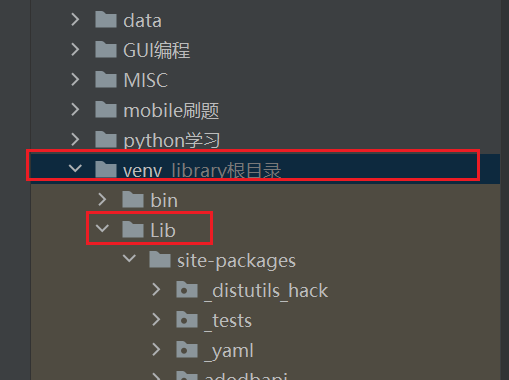
  • 一般来说都是使用pycharm作为python的开发环境，所以这里就说明一下pycharm中如何找到该源码(没下载的要先下载)，首先打开venv->Lib->这个目录

image-20250821211916677

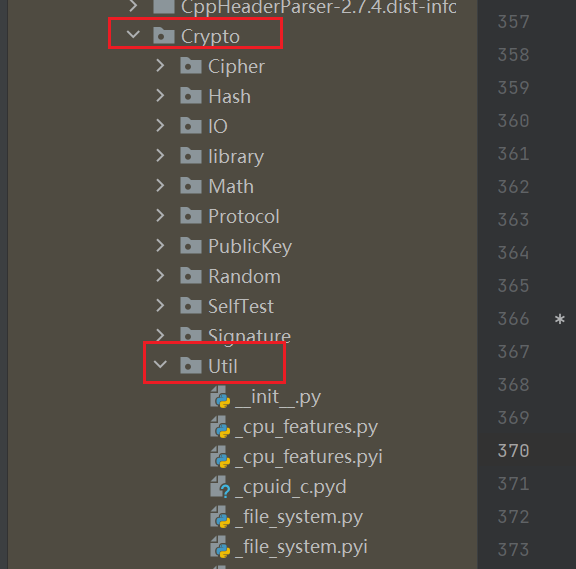
  • 然后找到Crypto这个包，再找到Crypto中Util这个子包

image-20250821212050368

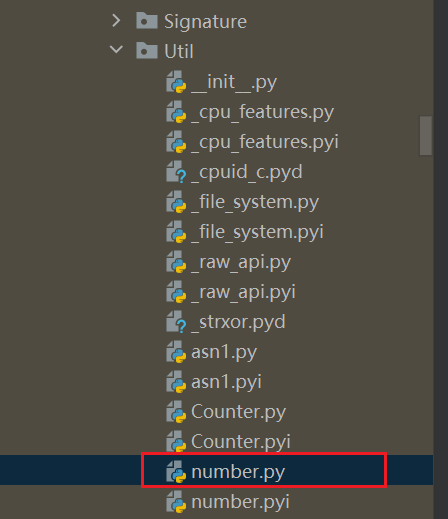
  • 最后找到number.py这个文件即可

image-20250821212141364

getPrime

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def getPrime(N, randfunc=None):
    """返回一个N位的素数.

    N必须是一个大于1的整数N must be an integer larger than 1.
    如果没有提供randfunc,则使用Random.get_random_bytes这个函数.
    """
    
    # 设置随机数生成器
    if randfunc is None:
        randfunc = Random.get_random_bytes
	# 检查N是否大于2
    if N < 2:
        raise ValueError("N must be larger than 1")
	
    # 随机生成一个数,并判断该数是否为素数,调用isPrime判断 
    while True:
        number = getRandomNBitInteger(N, randfunc) | 1
        if isPrime(number, randfunc=randfunc):
            break
    return number

isPrime

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def isPrime(N, false_positive_prob=1e-6, randfunc=None):
    r"""判断整数N是不是一个素数.

    Args:
        false_positive_prob (float):
          结果不是素数的统计概率,默认值为10^{-6}.
          注意，实际出现误判的概率远小于这个值
          这里只是数学上可以严格证明.
        randfunc (callable):
          一个随机数生成函数,它接收参数N,并返回一个长度为N的随机字节串
          如果没有提供该函数默认使用的是Crypto.Random.get_random_bytes这个函数,作为随机数生成算法

    Return:
    	如果输入的N是素数,则返回True
    """
    
	# 使用默认的随机数生成算法
    if randfunc is None:
        randfunc = Random.get_random_bytes
	# 当_fastmath这个库被调用的时候,就使用_fastmath库中的isPrime进行判断以提高效率
    if _fastmath is not None:
        return _fastmath.isPrime(long(N), false_positive_prob, randfunc)
	
    # 先判断N的是否为特殊的素数2
    if N < 3 or N & 1 == 0:
        return N == 2
    # 再判断p是否被sieve_base中的元素整除,或者是sieve_base中的元素
    # sieve_base存放的元素是2~104729之间所有的素数,包括2和104729
    for p in sieve_base:
        if N == p:
            return True
        if N % p == 0:
            return False
	# 最后先确定_rabinMillerTest检测的次数rounds,该检测的次数rounds为-ln(false_positive_prob)/ln(4)向上取整
    rounds = int(math.ceil(-math.log(false_positive_prob)/math.log(4)))
    # 最后使用_rabinMillerTest进行检测,并且_rabinMillerTest中才是调用randfunc算法的函数
    return bool(_rabinMillerTest(N, rounds, randfunc))

_rabinMillerTest

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def _rabinMillerTest(n, rounds, randfunc=None):
    """_rabinMillerTest(n:long, rounds:int, randfunc:callable):int
    测试n是否为素数
    返回值为0:n肯定是合数
    返回值为1:n很可能是素数
    返回值为2:n肯定是素数

    如果未提供randfunc,则使用Random.new.read

    这个函数仅供内部使用,未来可能会被重命名或删除
    """
    # 检测特殊的情况(n==2, n even, n < 2)
    if n < 3 or (n & 1) == 0:
        return n == 2
    # n可能是一个非常大的数,所以先计算n-1应该会更好
    n_1 = n - 1
    # 这一步就是将n-1转换为2**b * m的形式,b需要最大,m是奇数
    b = 0
    m = n_1
    while (m & 1) == 0:
        b += 1
        m >>= 1

    tested = [] # 存储被测试过的随机数,以免之后随机数再次生成到被测试过的数
    # 做最多n-2次判断
    for i in iter_range (min (rounds, n-2)):
        # 随机选择一个小于n的数a,确保它之前没有被测试过
        a = getRandomRange (2, n, randfunc)
        while a in tested:
            a = getRandomRange (2, n, randfunc)
        tested.append (a)
        # 接下来就是进行rabin-miller素性检验
        z = pow (a, m, n) # (a**m) % n
        if z == 1 or z == n_1:
            continue
        composite = 1
        for r in iter_range(b):
            z = (z * z) % n
            if z == 1:
                return 0
            elif z == n_1:
                composite = 0
                break
        if composite:
            return 0
    return 1