高等代数-线性方程组

• 参考教材：邱维声—高等代数大学高等代数课程创新教材

• 参考视频：北大丘维声教授清华高等代数课程1080P高清修复版(全151集)

前言

• 在学习高等代数之前，先对高等代数有一定的了解。高等代数研究的核心其实是其实是解方程，解多元一次方程以及解一元多次方程，再拓展到n元n次方程。这就是高等代数主要研究的内容。
• 书中前言这张图片对高等代数的概括非常好，研究的方向就是这两大线
  • 研究解多元一次方程的问题引入了矩阵、向量、线性空间等线性代数相关的内容，在线性代数中最关键的其实是线性空间、线性映射
  • 研究解一元多次方程的问题引入了群、环、域，最终形成了抽象代数这一门学科，而抽象代数的核心定理其实是伽罗瓦大定理

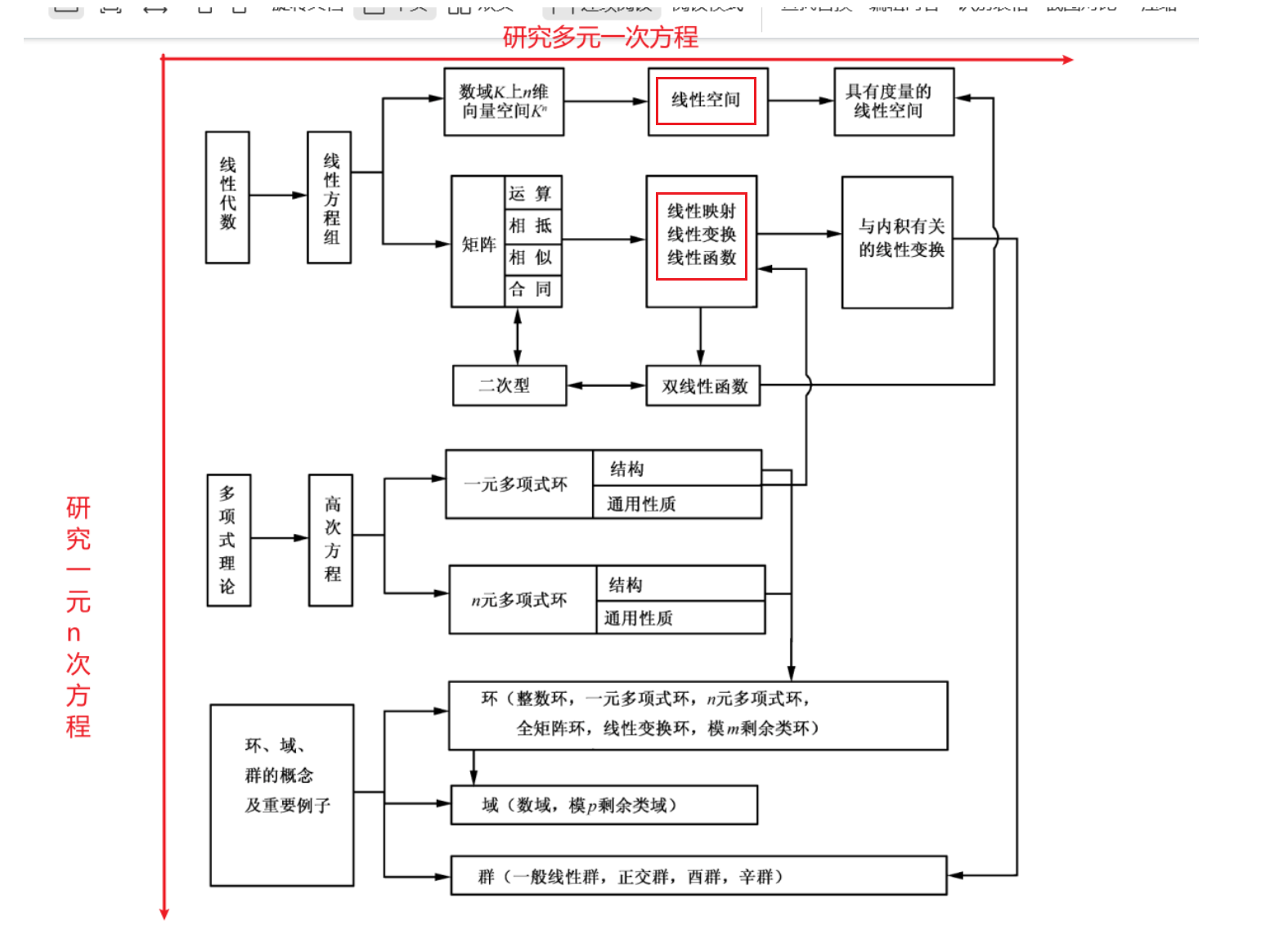
• 邱维声老先生的这本书的主线其实是：研究线性空间和多项式环的结构及其态射（线性映射，多项式环的通用性质），所以高等代数更多的是研究线性代数以及多项式环，而群和域这边是在抽象代数去研究。

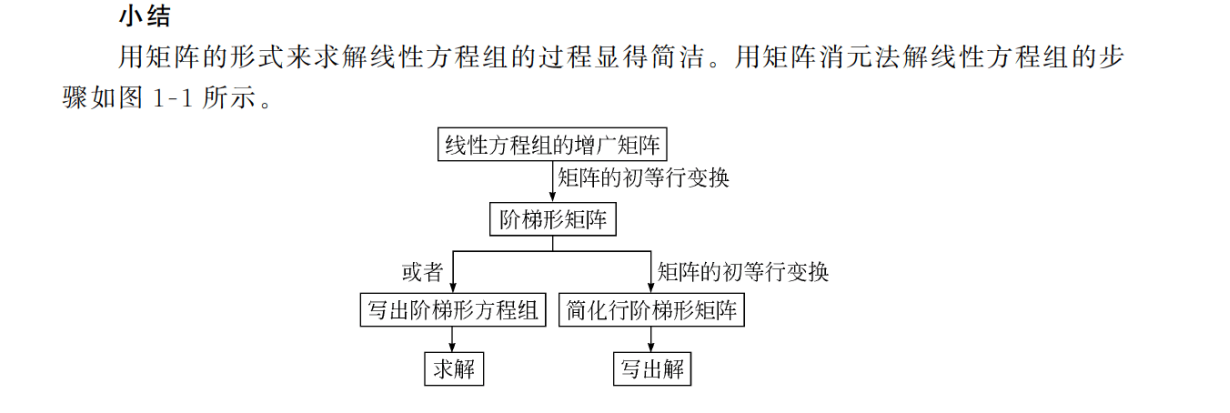
线性方程组矩阵消元法

线性方程组与矩阵

线性方程：

像$a_{1}x_1+a_2x_2+…+a_nx_n=b_1$这样，左端都是未知量$x_1,x_2,…,x_n$的一个齐次式，右端是常数被称为线性方程。

• 系数：每个未知量前面的数称为系数
• 常数项：右端的项被称为常数项

线性方程组：

两个及以上的线性方程组合，就被称为线性方程组，含n个未知量的线性方程组被称为n元线性方程组，它的一般形式如下：

• $a{11},a{12},…,a_{sn}$是系数
• $b_1,b_2,…,b_n$是常数项，一般写在等号右边
• 方程个数为s与未知量个数n可以相等，也可以是s<n或者s>n的关系
• 将$x_1,x_2,…,x_n$代入$c_1,c_2,…,c_n$后，每个方程都变成恒等式，那么这n元有序数组$(c_1,c_2,…,c_n)$是线性方程组的一组解，方程组的所有解组成的几何称为这个方程组的解集。

$$\begin{cases} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n &= b_1 \\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n &= b_2\\ ~~~~~~\vdots~~~~~~~~~~~~~\vdots~~~~~~~~~~~~~~~~~~~~\vdots&~~~~~~\vdots\\ a_{s1}x_1+a_{s2}x_2+...+a_{sn}x_n&=b_s \end{cases}$$

矩阵：由于解方程都是对系数和常数项操作并没有改变未知数，所以为了方便就引入了一个数表即矩阵，将方程组的未知数前面的系数和常数项提取出来。写成如下形式：

$$\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} & b_{1} \\ a_{21} & a_{22} & \dots & a_{2n} & b_{2} \\ \vdots & \vdots & \ddots& \vdots & \vdots \\ a_{s1} & a_{s2} & \dots & a_{sn} & b_{s} \end{bmatrix}$$

系数矩阵：只提取方程组的系数做为一个矩阵，这样的矩阵叫做系数矩阵

$$\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots& \vdots \\ a_{s1} & a_{s2} & \dots & a_{sn} \end{bmatrix}$$

增广矩阵：提取方程组的系数和常数项做为一个矩阵，这样的矩阵叫做增广矩阵

$$\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} & b_{1} \\ a_{21} & a_{22} & \dots & a_{2n} & b_{2} \\ \vdots & \vdots & \ddots& \vdots & \vdots \\ a_{s1} & a_{s2} & \dots & a_{sn} & b_{s} \end{bmatrix}$$

矩阵的定义：

由s·m个数排成s行、m列的一张表称为一个s×m矩阵，其中的每一个数称为这个矩阵的一个元素，第i行与第j列交叉位置的元素称为矩阵的(s,j)元。

注解1：矩阵通常用大写英文字母$\mathbf{A,B,C,…}$表示。一个s×m矩阵可以简单地记作$\mathbf{A}{s×m}$，它的(i,j)元记作$\mathbf{A}(i;j)$，如果矩阵$\mathbf{A}$的(i,j)元是$a{ij}$，那么可以记作$\mathbf{A}=(a_{ij})$

注解2：元素全为0的矩阵称为零矩阵，简记作$\mathbf{0}$。s行m列的零矩阵可以记成$\mathbf{0}_{s×m}$

注解3：如果一个矩阵$\mathbf{A}$的行数与列数相等，则称它为方阵。m行n列的方阵也称为m级矩阵

注解4：对于两个矩阵$\mathbf{A,B}$，如果它们的行数相等，都等于s；列数相等，都等于m；并且$\mathbf{A}(i;j)=\mathbf{B}(i;j),i=1,2,…,s,~~~j=1,2,…,m$，那么称矩阵$\mathbf{A,B}$相等，记作$\mathbf{A=B}$

例题1：解方程组

$$\begin{cases} x_1+3x_2+x_3&=2\\ 3x_1+4x_2+2x_3&=9\\ -x_1-5x_2+4x_4&=10\\ 2x_1+7x_2+x_3&=10 \end{cases}$$

1. 先使用2式+1式·(-3)、3式+1式、4式+1式·(-2)，消去2、3、4式的$x_1$，然后交换2式和4式的位置

2. 再使用3式+2式·2、4式+2式·5，以及4式+3式·2得到了一个阶梯型方程组

$$\begin{cases} x_1+3x_2+x_3&=2\\ ~~~~~~~~~~~x_2-x_3&=-3\\ ~~~~~~~~~~~~~~~~~~~~x_3&=6\\ ~~~~~~~~~~~~~~~~~~~~~0&=0 \end{cases}$$

1. 最后使用$3式·\frac{1}3{}$、1式+3式·(-1)、2式+3式、1式+2式·(-3)就可以得到简化阶梯形方程组，并且可以看出该方程组的解为$(3,-1,2)’$

$$\begin{cases} x_1~~~~&=3\\ ~~~~~~x_2&=1\\ ~~~~~~~~~~~~~x_3&=2\\ ~~~~~~~~~~~~~~0&=0 \end{cases}$$

线性方程组求解与矩阵化简

线性方程组的初等变换：

1. 把一个方程的倍数加到另一个方程上
2. 互换两个方程的位置
3. 用一个非零数称某一个方程

注解：通过线性方程组初等变换后的方程组的解与原方程组相同，所以使用有限次数的线性方程组的初等变换就可以求出n元线性方程组的解。

矩阵的初等行变换：

由于矩阵是线性方程组抽象出来的，所以线性方程组的初等变换运用到矩阵就是矩阵的初等行变换

1. 把一行的倍数加到另一行上
2. 互换两行的位置
3. 用一个非零数乘某一行

矩阵的行阶梯：

阶梯型方程组转换成矩阵形式，就变成了矩阵的行阶梯，有以下几个特征：

1. 元素全为0的行（称为零行）在下方(如果有零行)；
2. 元素不全为0的行（称为非零行），从左边数起第一个不为0的元素称为主元，它们的列指标随着行指标的递增而严格增大。即行指标增大1，列指标也需要增大1而不是增大2

$$\begin{bmatrix} 1&3&1&2\\ 0&1&-1&-3\\ 0&0&3&6\\ 0&0&0&0 \end{bmatrix}$$

简化行阶梯形矩阵：

简化阶梯形方程组抽象成矩阵形式就变成了简化行阶梯形矩阵，特点如下：

1. 它阶梯形矩阵
2. 每个非零行的主元都是1
3. 每个主元所在的列的其余元素都是0

$$\begin{bmatrix} 1&0&0&3\\ 0&1&0&-1\\ 0&0&1&2\\ 0&0&0&0 \end{bmatrix}$$

定理1：

任意一个矩阵都可以经过一系列初等行变换化成阶梯型矩阵

推理1：

任意一个矩阵都可以经过一系列初等行变换化成简化行阶梯形矩阵

矩阵解线性方程组：

将方程组转换为增广矩阵后，通过初等行变换化成阶梯型矩阵，再化成简化行阶梯形矩阵就是解线性方程组。

例题2：使用矩阵解方程组

$$\begin{cases} x_1+3x_2+x_3&=2\\ 3x_1+4x_2+2x_3&=9\\ -x_1-5x_2+4x_4&=10\\ 2x_1+7x_2+x_3&=10 \end{cases}$$

线性方程组解的情况与判别

线性方程组解的情况：

系数和常数项为有理数（或实数，或复数）的n元线性方程组的解的情况有且只有三种可能：无解，有唯一解，有无穷多个解。

注解：如果一个线性方程组有解，那么称它是相容的；否则，称它是不相容的

线性方程组解的判别：

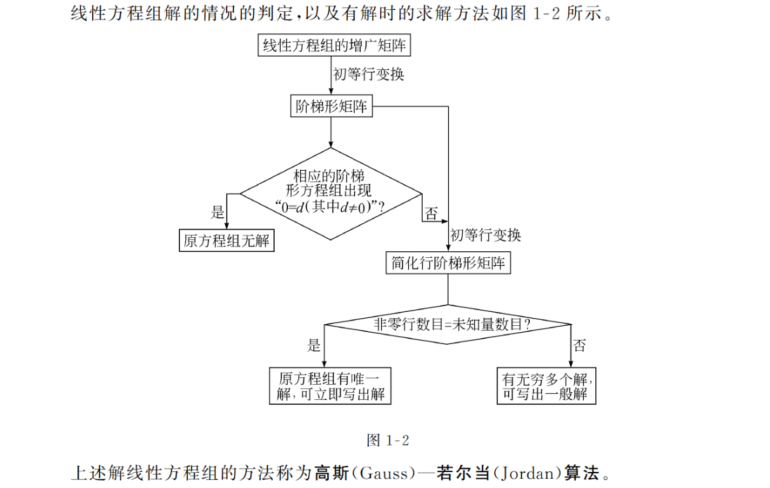
把n元线性方程组的增广矩阵经过初等行变换化成阶梯形矩阵，如果相应的阶梯型方程组出现0=d(其中d是非零数)，这种方程，那么原方程无解；否则，有解。

当有解的时候，如果阶梯形矩阵的非零行数目r等于未知量数目n，那么原方程组有唯一解，如果r<n那么原方程有无穷多个解。

注解：当原方程有无穷多个解的时候，简化的行阶梯形矩阵就会出现如下形式

$$\begin{bmatrix} 1&-1&0&2\\ 0&0&1&-1\\ 0&0&0&0 \end{bmatrix}$$

转换成线性方程组后就如下：

$$\begin{cases} x_1-x_2&=2\\ x_3&=1\\ 0&=0 \end{cases}$$

之后化简就如下,下面表达式其实就是原线性方程组的一般解，其中行阶梯矩阵对应的主元为系数的未知量$x_1,x_3$称为主变量，其余未知量$x_2$称为自由未知量：

$$\begin{cases} x_1&=x_2+2\\ x_3&=1\\ 0&=0 \end{cases}$$

齐次线性方程组：

常数项全为0的线性方程组称为齐次线性方程组。(0,0,...,0)是齐次线性方程组的一个解，称为零解。其余的解（如果有）称为非零解。该方程如下图所示，由于常数项全为0，所以在将其转换为矩阵的求解时，只需要使用系数矩阵即可：

$$\begin{cases} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n &= 0 \\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n &= 0\\ ~~~~~~\vdots~~~~~~~~~~~~~\vdots~~~~~~~~~~~~~~~~~~~~\vdots&~~~~~~\vdots\\ a_{s1}x_1+a_{s2}x_2+...+a_{sn}x_n&=0 \end{cases}$$

推论1：n元齐次线性方程组有非零解的充分必要条件是：它的系数矩阵经过初等行变换化成的阶梯形矩阵中，非零行的数目r<n

推论2：n元齐次线性方程组，如果方程组的数目s小于未知量的数目n，那么它一定有非零解。

高斯-若尔当算法：

数域

定义1：

复数集的一个子集K如果满足，那么就称K是一个数域，有理数集Q，实数集R，复数集C都是数域：

1. $0,1\in K$
2. $a,b\in K \Rightarrow a\pm b,ab\in K$，$a,b\in K,b\not=0 \Rightarrow \frac{a}{b}\in K$

注解1：复数域是最大的数域。在讨论线性方程组有没有解时，都是在一个给定的数域K里讨论，称数域K上的线性方程组，即它的系数和常数项都属于K，且它的解（若存在）是K中的数组成的有序数组。

注解2：讨论矩阵问题时，也是在一个给定的数域K里进行，称数域K上的矩阵。

命题1：

任一数域都包含有理数域

补充题(未完成)

• 补充题想了有点久暂时不想，先鸽这边。有灵感就马上写了。

1. 解下列线性方程组。

$$\begin{cases} (1+a_1)x_1+x_2+x_3+...+x_n&=b_1\\ x_1+(1+a_2)x_2+x_3+...+x_n&=b_2\\ \dots~~~\dots~~~\dots~~~\dots~~~\dots~~~\dots&\dots\\ x_1+x_2+x_3+...+(1+a_n)x_n&=b_n \end{cases}$$

1. 解下列线性方程组

$$\begin{cases} x_1+2x_2+3x_3+...+(n-1)x_{n-1}+nx_n&=b_1\\ nx_1+x_2+2x_3+...+(n-2)x_{n-1}+(n-1)x_n&=b_2\\ \dots~~~\dots~~~\dots~~~\dots~~~\dots~~~\dots~~~~~\dots\\ 2x_1+3x_2+4x_3+...+nx_{n-1}+x_n&=b_n \end{cases}$$

1. 解下列方程组

$$\begin{cases} x_1+x_2+...+x_n&=1\\ ~~~~~~~~~x_2+...+x_{n}+x_{n+1}&=2\\ ~~~~~~~~~~~~~~~\dots~~~\dots~~~\dots~~~\dots~~~\dots~~~\dots~~~~~\dots\\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x_{n+1}+x_{n+2}+...+x_{2n}&=n+1 \end{cases}$$