LFSR伪随机数生成器

• 参考博客：3.6 线性反馈移位寄存器（LFSR） | 第三章：序列密码 |《密码学入门》| Python 技术论坛

• 参考博客：线性反馈移位寄存器 - 维基百科，自由的百科全书

• 参考博客：线性反馈移位寄存器（LFSR） - 生活的高手 - 博客园

• 参考博客：cdcq的密码学教程四——BM算法 | cdcq

• LFSR英文名为Linear feedback shift register，中文翻译过来就是线性反馈移位寄存器，其伪随机数生成的特点已经包含在LFSR的名称中，也就是线性、反馈这两个词。

• 由于LFSR是非常容易使用硬件实现的，所以在以前很多流密码的密钥都是通过LFSR伪随机数生成算法来实现的，但是该伪随机数生成的算法在密码学体制中是比较不安全的，容易被预测到。但是LFSR组合其实可以得到安全的流密码。

• 本篇文章写于2025.6.16但是写的不怎么好，而在2025.9.11在图书馆随便看看，看到了这本书，从数学原理讲LSFR，于是决定重写博客，重新学习LSFR相关的。

LFSR

• LFSR是指给定前一状态的输出，将该输出的线性函数在用作输入的移位寄存器。
• 其中异或运算是最常见的单比特线性函数，对寄存器的某些位进行异或操作后作为输入，再对寄存器中的各比特进行整体移位。也就是先进行异或运算再进行位移运算

LFSR的两种形式

• LFSR其实不止上面介绍的一种方式，其实还有另一种方式。
• 对于上面介绍的这种，是比较经典的，将其称为Fibonacci型，其实就是指定抽头影响输入位。

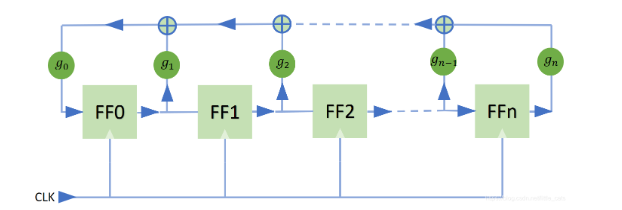
• 还有一种LFSR类型，该类型为Galois型，这种类型是输出位送给输入位后逐位异或，从而影响其他位，得到伪随机。

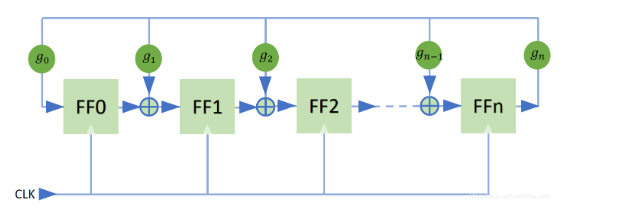
LFSR算法描述(Fibonacci型)

• 我们先来给出一张图片，这张图片就简单介绍了LFSR算法。这张图主要做了一下几个事情：

  • 对于初始的状态$a_na_{n-1}...a_{2}a_{1}$，经过一个线性函数$f(a_1,a_2,...,a_n)$的运算，其实$f(a_1,a_2,...,a_n)$这个线性函数就是异或操作，即$f(a_1,a_2,...,a_n)=a_1\oplus a_2 \oplus ...\oplus a_n$,得到一个结果作为我们后续的输入的bit值，所以这个函数运算结果只有0或者1，先暂时保存这个值

  • 之后将$a_na_{n-1}...a_2a_1$经过位移后整体就变成$a_{n-1}a_{n-2}...a_1a_0$，此时$a_0$其实就是作为输出值了

  • 最后我们再将$f(a_1,a_2,...,a_n)$运算得到的结果传递给$a_n$，此时就构成了新的一组$a_na_{n-1}...a_2a_1$序列

  • 之后像这样不断的线性位移计算，我们就能得到这些二进制序列，我们每线性位移n次取一次序列，这样就得到了n位伪随机数

  • 注意：不一定所有的位都参与线性运算，一般只选择几个位参与线性运算

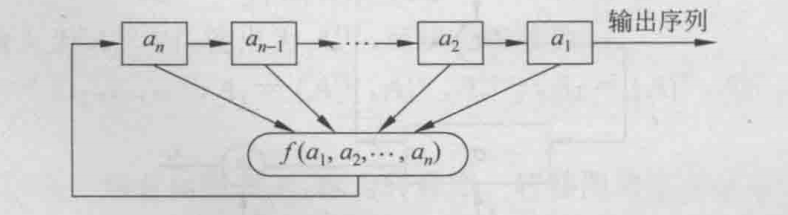
有几个注意点：

1. 将参与线性运算$f(a_1,a_2,...,a_n)$的位称为抽头，也就是LFSR状态下影响输入的位
2. LFSR最右边的位为输出位，同时它始终也是抽头。
3. 抽头是有顺序的异或，然后反馈到最左边的位。
4. 最右边的位序列称为输出流，如上图所示其实我们的输出流其实是$a_1$先输出出来,然后$a_2$，最后才是$a_n$
5. 最大长度LFSR产生m序列具有$2^m-1$种状态，寄存器全零状态的时候线性位移后还是全零

• 接下来我们使用Python实现一下简单的32位LFSR伪随机数：

def _int32(x):
    return x & 0xFFFFFFFF

class LFSR:
    def __init__(self,seed):
        # seed作为初始化寄存器的一个种子
        # 规定二进制序列是这样的an an-1 ... a2 a1与上图描述一致
        self.seed = _int32(seed)

    def xor(self):
        # 规定a26 a16 a11 a1都作为抽头
        x = bin(self.seed)[2:].zfill(32)
        tap = [25,15,10,0]
        tmp = 0
        for i in tap:
            tmp ^=int(x[i],2)
        return tmp

    def lshift(self,an,reg):
        # 进行位移运算
        return _int32((an<<31)|(reg>>1))

    def LSF(self):
        # 生成32位的随机数
        # 其实也可以直接LSF一次,而不用32次
        for i in range(32):
            an = self.xor()
            self.seed=self.lshift(an,self.seed)
        return self.seed

LFSR = LFSR(0xF75a15663499)
for i in range(10):
    print(LFSR.LSF())

LFSR数学表示(Fibonacci型)

• LFSR有三种数学表示分别是递推公式、多项式表示、矩阵表示，其转换为数学符号，在有的时候更有利于推导公式之类的。

• 首先我们来介绍这张图所有位都参与异或的情况：

  • 设初始序列为$a_{n-1}a_{n-2}...a_1a_0$，由于我们每个位都参与运算，所以每个位都影响了最终结果
  • 所以此时我们就可以写成这样一个模2的方程$a_{n+1}=a_{n}+a_{n-1}+...+a_2+a_1~mod~2$
  • 此时我们还可以使用多项式的形式来表示$P(x)=x^{n}+x^{n-1}+...+x^{2}+x+1~mod~2$

• 对于上图我们还可以使用矩阵来表示，我们可以定义状态向量$A_n$和转移矩阵$B_n$

$$A_n=\begin{bmatrix}a_n\\a_{n-1}\\ \vdots \\ a_2 \\ a_1 \end{bmatrix}\\ B_n=\begin{bmatrix}1&&1 && \cdots &&1 &&1\\ 1 && 0 && \cdots && 0 && 0\\ 0 && 1 && \cdots && 0&&0\\ \vdots && \vdots && \ddots && \vdots && \vdots\\ 0 && 0 && \dots &&1&&0 \end{bmatrix}$$

• 最后得到结果

$$A_{n+1}=B_nA_n=\begin{bmatrix}a_n+a_{n-1}+...+a_2+a_1~mod~2\\a_n\\ \vdots \\ a_3 \\ a_2 \end{bmatrix}$$

• 但是由于在设计LFSR的时候我们并不会每一位都参与异或，此时我们就在$a_i$的前面添加一个系数，如果该位是抽头的话$a_i$前面的系数就为1，该位不是抽头的话$a_i$前面的系数就是0
• 例如上面使用Python编写的LFSR，就选用的是$a_{26}、a_{16}、a_{11}、a_{1}$作为抽头这样的话，就可以使用数学表达式得到这么一个序列

$$a_{n+1}=a_{26}+a_{16}+a_{11}+a_1~mod~2\\ P(x)=x^{26}+x^{16}+x^{11}+x+1~mod~2$$

• 使用矩阵表示就如下，$B_n$太大写不下：

$$A_n=\begin{bmatrix}a_{32}\\a_{31}\\ \vdots \\ a_2 \\ a_1 \end{bmatrix}\\$$

• 最后的结果要如下：

$$A_{n+1}=B_nA_n=\begin{bmatrix}a_{26}+a_{16}+a_{11}+a_1~mod~2\\a_{32}\\ \vdots \\ a_3 \\ a_2 \end{bmatrix}$$

• 所以归纳出输出序列，执行第m次的线性位移操作后的输出值的递推如下：

$$a_{i+m}=\sum^{m+1}_{j=0}p_j *a_{i+j}~mod~2\\s_i,p_i\in\{0,1\},i=0,1,2,...$$

• 多项式表示为，如果第i位为抽头$p_i$就为1，否则为0：
• 这里注意有的多项式表达最高次数位始终为1，但是这里我们是将最低次数位默认为输出位，所以这里多项式始终有个1，具体情况再具体定义这个多项式就行了

$$P(x) = p_{n-1}x^{n-1}+p_{n-2}x^{n-2}+...+p_{2}x^{2}+p_1x+1~mod~2$$

• 最后矩阵状态转移就不写了，写矩阵太麻烦了。

LFSR的逻辑图(Fibonacci型)

• 由于LFSR的特性，其是比较容易在硬件中实现的，逻辑电路图并不复杂。其组成其实就是n个触发器，加上一些异或门再通过导线连接即可得到一个硬件的LFSR。
• 如下图所示：

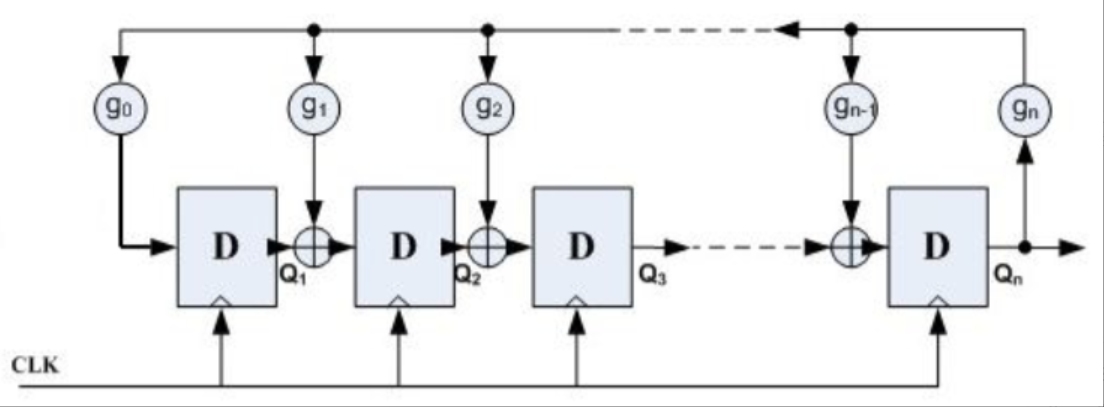
LFSR破解

• 对于LFSR的破解需要用上一个经典的算法也就是 Berlekamp-Massey算法。这里建议先去学习一下Berlekamp-Massey算法，先从它的数学抽象出来的问题入手，在破解LFSR的时候会更有助于理解。Berlekamp–Massey 算法 - OI Wiki
• 对于Berlekamp-Massey算法，就不在这里详细介绍，这里只介绍Berlekamp-Massey算法在破解LFSR中的应用。

LFSR深入理解

• 接下来要介绍一些相关的定义和定理作为学习Berlekamp-Massey算法的前置知识。

知识点1

假设一个LFSR长度为L，LFSR的最初状态其实就等于LFSR所产生的序列的前L位输出。如下图所示，序列$a_0、a_1、...、a_n$其实就是长度为N的LFSR的初始状态。

从第$L+1$位开始的所有输出，完全由LFSR的反馈结构和初始状态决定，说明了一旦LFSR的反馈结构确定并且设置了初始状态，那么输出序列就唯一确定

知识点2

当我们要用阶(其实是LFFR的长度)为L的LFSR，来生成长度为$N$的序列其实会出现以下两种情况：

1. 当L>=N时，该LFSR一定能生成长度为$N$的序列，但是并不是最短的一个LFSR
2. 当L<N时，如果该LFSR能生成长度为$$N$$的序列，那么从第$L+1$位开始就必须满足递推式$s_n=\sum^{L}_{i=1}c_{i}s_{n-i}~mod~2$

定理1:

如果某个长度为L的LFSR能生成长度为N的序列，$s_0、s_1、...、s_{N-1}$,但是无法生成第$s_{N}$项，那么任何一个可以完整生成序列$s_0、s_1、...、s_{n}$的LFSR，其长度必须满足$L^{'}≥N+1-L$，这个其实是B-M算法的下界定理

引理:

如果一个长度为n的LFSR记为$L_{n}(s)$，生成了$s_0,s_1,...,s_{N-1}$但是该LFSR并不能生成$s_0,s_1,...,s_{n-1},s_{n}$，那么就有$L_{n+1}(s)≥max[L_{N}(s),N+1-L_{N}(s)]$

定理2:

如果一个长度位N的LFSR