格密码之LWE
-
参考文章：微信公众平台
-
注意：虽然LWE是属于格密码，但是并非所有的LWE题型都是用格的方法求解最近向量的，可能还有其他非格的方法可以求解。
知识回顾
矩阵表示方程组
- 在学习线性代数和高等代数的时候我们一开始就需要了解矩阵。（当然某些编排不好的书一开始的内容就是行列式）。对于下面一个线性方程组，由于解方程的时候只有未知数前面的系数在改变，未知数的次数是不变的。
$$
\begin{cases}
a_{11}x_1+a_{12}x_2+…+a_{1n}x_n &= b_1 \
a_{21}x_1+a_{22}x_2+…+a_{2n}x_n &= b_2\
a_{s1}x_1+a_{s2}x_2+...+a_{sn}x_n&=b_s
\end{cases}
$$
+ 为了更方便书写，我们直接把线性方程组中的未知数省略掉，形成一个$s×n$的矩阵。
+ 其中$s$表示的是这个矩阵有$s$行，也表示这个线性方程组中方程的个数。
+ 其中$n$表示的是这个矩阵有$n$列，也表示这个线性方程组未知数的个数。
$$
\begin{bmatrix}
a_{11} & a_{12} & \dots & a_{1n} \\
a_{21} & a_{22} & \dots & a_{2n} \\
\vdots & \vdots & \ddots& \vdots \\
a_{s1} & a_{s2} & \dots & a_{sn}
\end{bmatrix}_{s×n}
$$
## 向量表示方程组
+ 如下图所示的个向量的线性方程组，我们可以使用一个列向量来表示方程组中每个方程中相同未知数的系数。
$$
\begin{cases}
a_{11}x_1+a_{12}x_2+...+a_{1n}x_n &= b_1 \\
a_{21}x_1+a_{22}x_2+...+a_{2n}x_n &= b_2\\
~~~~~~\vdots~~~~~~~~~~~~~\vdots~~~~~~~~~~~~~~~~~~~~\vdots&~~~~~~\vdots\\
a_{s1}x_1+a_{s2}x_2+...+a_{sn}x_n&=b_s
\end{cases}
$$
+ 对于那么对于上面这个方程组，分别使用列向量$\alpha_1,...,\alpha_n$表示相同未知数前面的系数的集合，使用$\beta$表示常数，那么方程组就可以使用向量更简单的表示出来：
$$
\alpha_1=\begin{pmatrix}
a_{11} \\
a_{21} \\
... \\
a_{s1}
\end{pmatrix},....,
\alpha_n=\begin{pmatrix}
a_{1n} \\
a_{2n} \\
... \\
a_{sn}
\end{pmatrix}
,\beta=\begin{pmatrix}
b_{1} \\
b_{2} \\
... \\
b_{s}
\end{pmatrix}
\\
\\
x_1\alpha_1+.....+x_n\alpha_n=\beta
$$
## 矩阵乘法表示方程组
+ 在学习了矩阵、向量、矩阵乘法之后，对于如下的一个线性方程组，其实可以使用矩阵乘法来表示出来。
$$
\begin{cases}
a_{11}x_1+a_{12}x_2+...+a_{1n}x_n &= b_1 \\
a_{21}x_1+a_{22}x_2+...+a_{2n}x_n &= b_2\\
~~~~~~\vdots~~~~~~~~~~~~~\vdots~~~~~~~~~~~~~~~~~~~~\vdots&~~~~~~\vdots\\
a_{s1}x_1+a_{s2}x_2+...+a_{sn}x_n&=b_s
\end{cases}
$$
+ 可以使用一个$s×n$的矩阵乘一个$n×1$的矩阵，以及$s×1$的矩阵表示这个线性方程组，如下所示：
$$
\begin{bmatrix}
a_{11} & a_{12} & \dots & a_{1n} \\
a_{21} & a_{22} & \dots & a_{2n} \\
\vdots & \vdots & \ddots& \vdots \\
a_{s1} & a_{s2} & \dots & a_{sn}
\end{bmatrix}_{s×n}×
\begin{bmatrix}
x_{1} \\
x_{2} \\
\vdots \\
x_{n}
\end{bmatrix}_{n×1}=\begin{bmatrix}
b_{1} \\
b_{2} \\
\vdots \\
b_{s}
\end{bmatrix}
$$
# LWE初步介绍
## 问题引入鸡兔同笼正常版
首先来看一下鸡兔同笼的问题，鸡兔同笼问题出自于`《孙子算经》`，具体问题如下：
1
有鸡、兔同笼，上有三十五头，下九十四足。问雉、兔各几何？
+ 我们可以使用穷举法，从0只鸡开始，然后一直到35只鸡，直到找到脚的数量符合题目的要求即可。
+ 但是穷举法是偏离今天的`LWE`的内容的，所以主要介绍的是另一种方法，也就是代数方法——解方程。首先确定位置量，鸡、兔的个数我们是不知道的，那就设鸡为$x_1$，兔为$x_2$，那么就可以列出如下的一个二元一次方程组：
$$
\begin{cases}
x_1+x_2&= 35 \\
2x_1+4x_2&= 94\\
\end{cases}
$$
+ 将这个方程组使用矩阵表示就是如下的形式：
$$
\begin{bmatrix}
1 & 1 \\
2 & 4 \\
\end{bmatrix}_{2×2}×\begin{bmatrix}
x_{1} \\
x_{2} \\
\end{bmatrix}_{2×1}=\begin{bmatrix}
35 \\
94 \\
\end{bmatrix}
$$
+ 对于使用方程组的表示方法可以直接通过高斯消元法直接求出答案，而对于矩阵乘法表示可以通过左右两边乘一个左边方阵的逆矩阵，就可以得到结果。
## 问题引入鸡兔同笼误差版
+ 对于上面的鸡兔同笼问题，我们做一个修改。这里我们假设，在数透和脚的数量的时候，存在一个误差，这个误差满足某个概率分布，这里我们就假设数脚我们多数了一个，这样就会变成下面的这个方程
$$
\begin{cases}
x_1+x_2+e_1&= 35 \\
2x_1+4x_2+e_2&= 95\\
\end{cases}
$$
+ 此时我们不知道误差，所以我们列出的方程是这样的
$$
\begin{cases}
x_1'+x_2'&= 35 \\
2x_1'+4x_2'&= 95\\
\end{cases}
$$
+ 这个时候如果再使用高斯消元法去求解这个方程，那就会得到下面这个解
$$
\begin{cases}
x_1'= 22.5 \\
x_2'= 12.5\\
\end{cases}
$$
+ 这个结果出现了小数，显然是不正确的。因为存在一个误差值$e'=x-x'$是我们所不知道的东西。
## 引入LWE问题
+ 对于上面`鸡兔同笼误差版`（方程组中的每个方程带误差，并且误差我们不知道），这就是这篇文章要说明的一个`LWE`问题。
+ `LWE`英文全称为`learn with error`，翻译过来为容错学习。容错学习的具体描述如下：
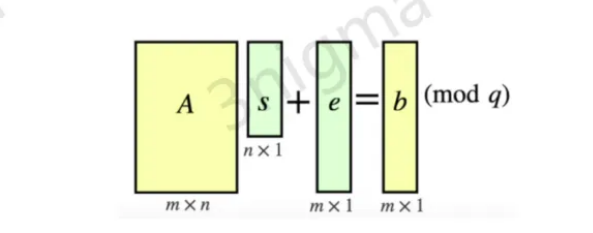
+ 设$n,m$以及$q$为整数（其中$q$一般为质数），并设$\mathbf{s}\in \Z_q^n$上的一个秘密向量，在$\Z_q^{m×n}$上均匀选取矩阵$\mathbf{A}$，设$X$为一个$\Z^m$上的概率分布，并在$Z^m$上选取一个分布服从$X$的小向量$e$作为噪声，并计算：
$$
\mathbf{b}=\mathbf{As}+\mathbf{e}~mod(~q)
$$
+ 并给出$(\mathbf{A},\mathbf{b})$，让我们还原出秘密向量$\mathbf{s}$，这就是最常见的`LWE`问题（这种LWE问题也被称为`搜索LWE问题`，即`Search-LWE`）。
>注解1：上面的$\Z_q^n$，表示的是数域`q`下的`n`维线性空间
>
>注解2：上面的$\Z_q^{m×n}$，表示的是数域`q`下的`m×n`矩阵，其维度是`mn`
>
>注解3：上面$\Z^m$表示数域$\Z$下的`m`维线性空间
>
>存疑：这里留个疑问，对于LWE的问题具体是如何定义的需要去看看论文，LWE、MLWE如何定义的感觉会搞混掉。还有就是从问题的形式出发，就出现了Search-LWE和Decisional-LWE。目前就以上面的问题来定义LWE。（总之一般的LWE问题就是要我们求出e或者b，这两个知道其中一个就可以知道另一个。）
+ 对于上述`LWE`问题，如果使用高斯消元法进行求解就会扩大误差`e`的影响，使得求出的解与原来的解误差非常大。所以高斯消元法在`LWE`问题中就体现不出太大的作用。
+ 这个时候如果我们知道$e$的界限，我们就可以通过搜索$\mathbf{s'}\in\Z^n_q$，如果搜索到$\mathbf{s'}\in\Z^n_q$使得$||\mathbf{As'}-\mathbf{b}||_{\infty}≤B$，其中B满足$||\mathbf{e}||_{\infty}≤B$，这个时候我们就说找到了满足LWE问题的一组解。
## 理解LWE问题
+ 接下来将用几张图片，通过几何直观的感受来理解`LWE`问题。在此之前，先来回顾一下格的定义：
$$
L(\mathbf{B})=\{\sum^{n}_{i=1}x_ib_i:x_i\in Z,i=1,...,n\}
$$
+ 在`LWE`这个方程中，$s_{n×1}$这个向量其实就是未知数，我们是不知道的，而$A_{m×n}$是一个矩阵，结合上面的格的定义，我们就将这个矩阵$A_{m×n}$拆分成$n$个列向量，每个列向量有$m$个元素。
$$
A_{m×n}=(\alpha_1,...,\alpha_n)
$$
+ 假设这些列向量线性无关，那么这$(\alpha_1,...,\alpha_n)$就构成了一个格，并且这个格的维数为`m`，而这个格的秩为`n`，就以下面这个方程组做例子通过几何直观来理解吧：
$$
\begin{cases}
x_1+x_2+0&= 10 \\
2x_1+4x_2+1&= 27\\
\end{cases}
$$
$$
\begin{cases}
x_1'+x_2'&= 10 \\
2x_1'+4x_2'&= 27 \\
\end{cases}
$$
$$
\begin{bmatrix}
1 & 1 \\
2 & 4 \\
\end{bmatrix}_{2×2}×\begin{bmatrix}
x_{1}' \\
x_{2}' \\
\end{bmatrix}_{n×1}=\begin{bmatrix}
10 \\
27 \\
\end{bmatrix}
$$
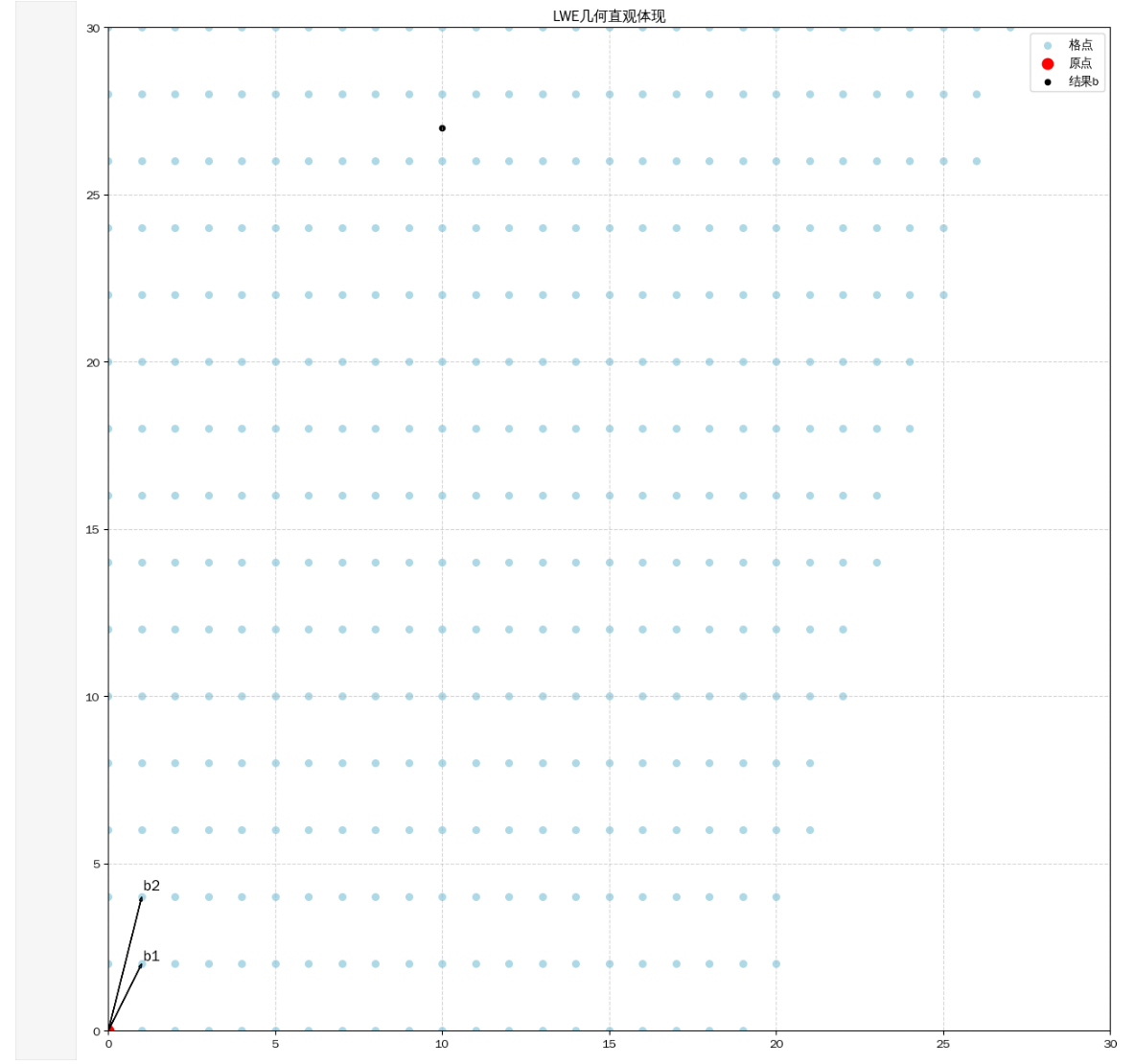
+ 对于上面的例子，格的基其实就是这两个列向量$\alpha_1=(1,2)^{T},\alpha_2=(1,4)^{T}$，接下来我们将这个格点画出来，并且将点$(10,27)$使用不同颜色的点也标在图中。
+ 注意：这里点$(10,27)$其实并不是在格点上，此时结合LWE的求解（也就是通过搜索$\mathbf{s'}\in\Z^n_q$，如果搜索到$\mathbf{s'}\in\Z^n_q$使得$||\mathbf{As'}-\mathbf{b}||_{\infty}≤B$，其中B满足$||\mathbf{e}||_{\infty}≤B$，这个时候我们就说找到了满足LWE问题的一组解。）以及最近向量问题形式，我们不难发现**Search-LWE**问题其实本质上就是**最近向量问题**
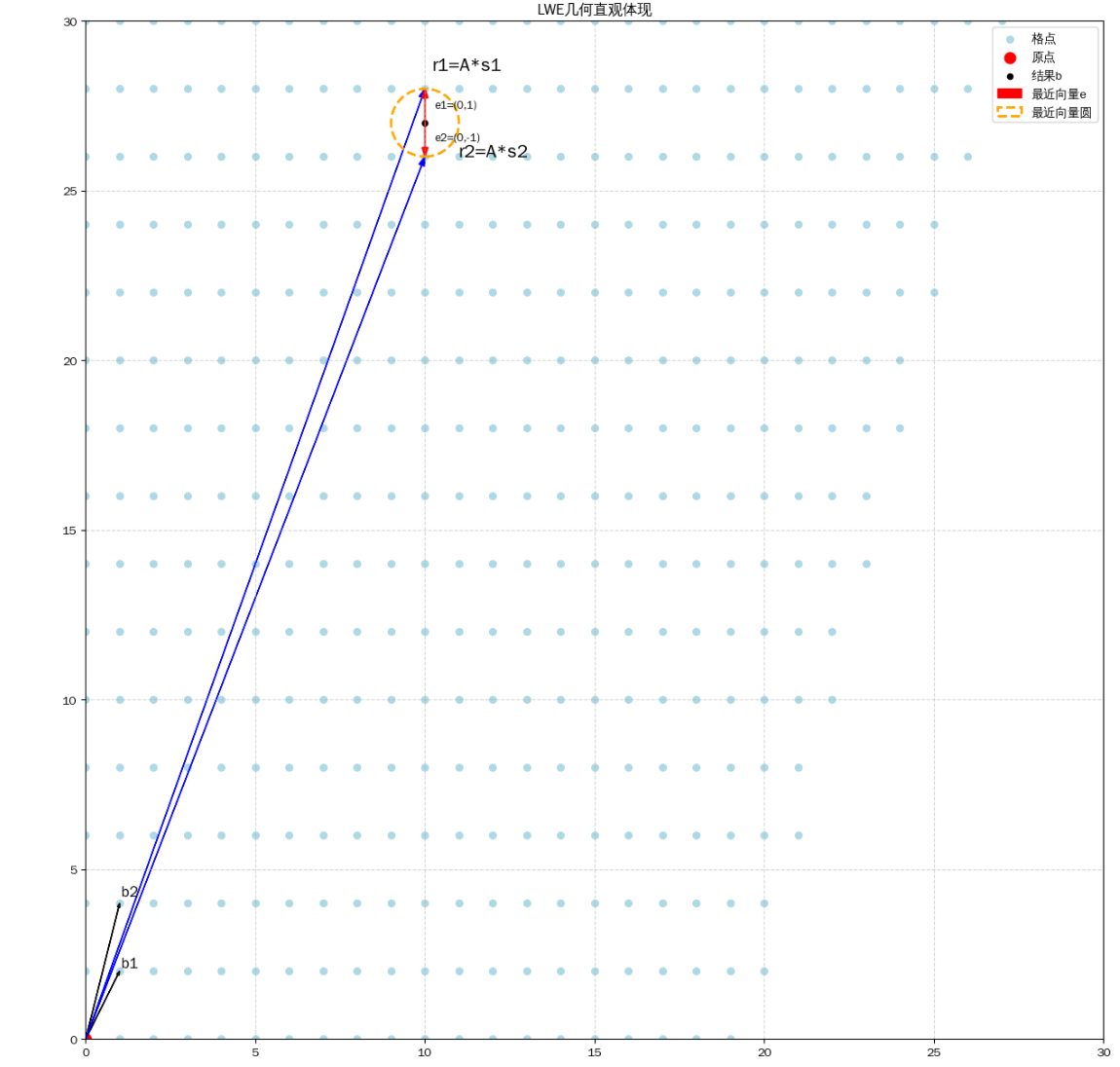
+ 从上图中我们可以看到，如果误差选取不好的话，就会出现多组解满足$||\mathbf{As'}-\mathbf{b}||_{\infty}≤B$，并且目前除了搜索之外没有什么特别快的求解方案。
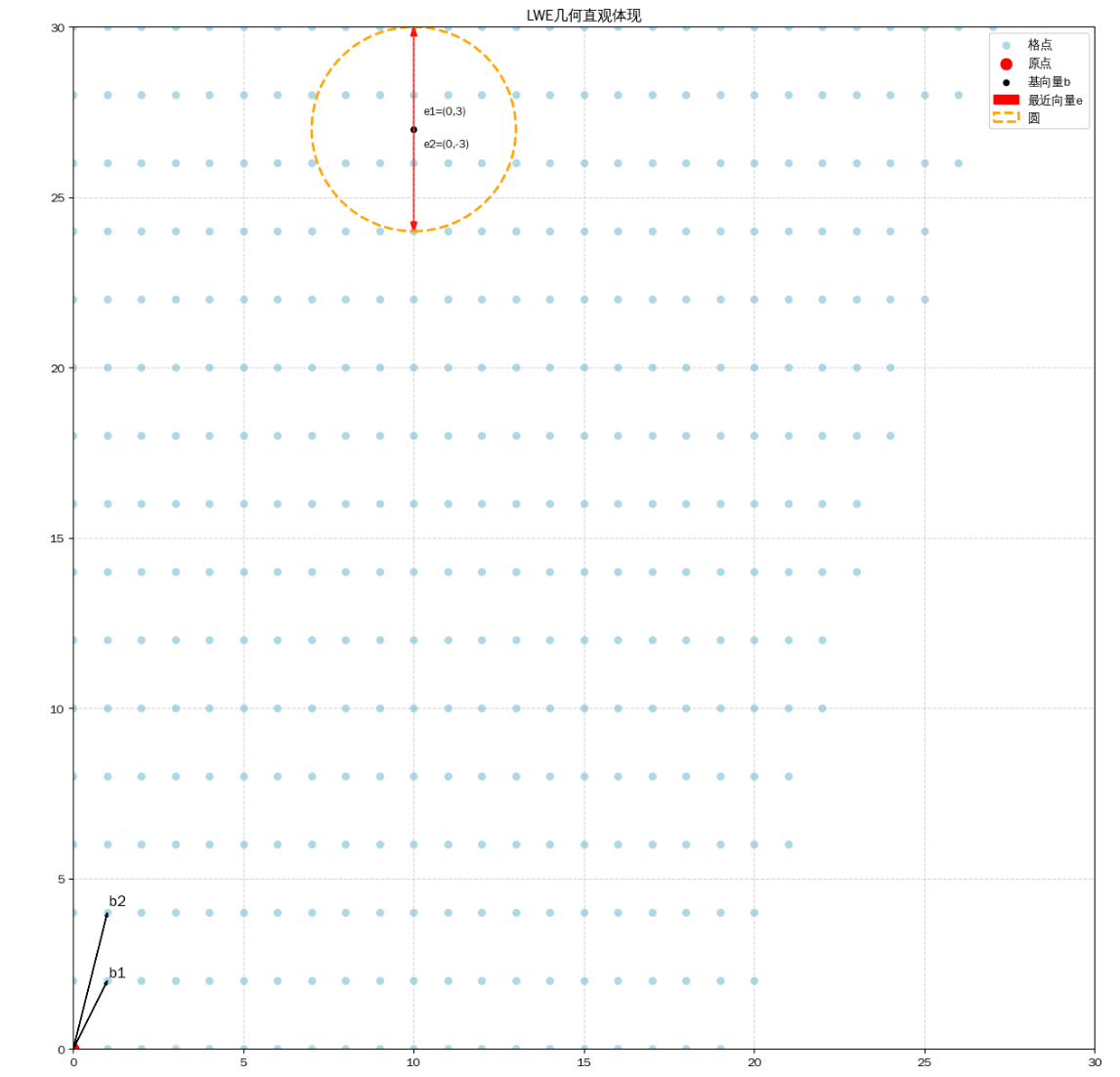
+ 接下来再看一个图片，下面这张图片所出现的情况是误差向量$\mathbf{e}$非常大的时候，以误差向量$\mathbf{e}$的长度为半径画出一个圆，在这个圆内会有非常多的点，而这些点都满足$||\mathbf{As'}-\mathbf{b}||_{\infty}≤B$，这就导致解不唯一，还需要我们在这些解中找到正确的解。
# LWE数学结构
> 通过上面的介绍我们其实可以了解到LWE其实就是在一些方程（或者其他类似于方程的代数结构）中添加一些错误，使得我们在不知道错误的情况下不能直接求解方程从而得到正确答案。
>
> 在上面介绍了方程形式的，方程形式的LWE是最简单的代数结构的LWE问题，接下来我们还要介绍其他代数结构的LWE问题，在介绍其他代数结构的LWE问题，先再描述一下普通的LWE问题。
## 普通LWE
## Module-LWE
>Module-LWE使用的代数结构也算是一个环，但并不是严格的环结构。并且Module-LWE中的Module指的并不是同余的那个模，指的是同余的模块的那个位置。问题的本质是模块结构（模块上的向量卷积结构）。接下来要介绍一下Module-LWE问题的具体形式。
## Ring-LWE
>Ring-LWE使用的代数结构算是一个比较严格的环结构，并且Ring-LWE强调的也是环结构。
# LWE困难问题
## Search-LWE
> 对于Search-LWE问题，在LWE初步介绍那边已经介绍的相当清楚了，这里看情况看看要不要再讲一遍。
+ `Search-LWE`问题的描述这里在简单说一下：
+ 设$n,m$以及$q$为整数（其中$q$一般为质数），并设$\mathbf{s}\in \Z_q^n$上的一个秘密向量，在$\Z_q^{m×n}$上均匀选取矩阵$\mathbf{A}$，设$X$为一个$\Z^m$上的概率分布，并在$Z^m$上选取一个分布服从$X$的小向量$e$作为噪声，并计算：
$$
\mathbf{b}=\mathbf{As}+\mathbf{e}~mod(~q)
$$
+ 并给出$(\mathbf{A},\mathbf{b})$，让我们还原出秘密向量$\mathbf{s}$，这就是最常见的`LWE`问题（这种LWE问题也被称为`搜索LWE问题`，即`Search-LWE`）。
+ `Search-LWE`问题是比较常见的一个LWE问题，在CTF中的很多题目基本上都是`Search-LWE`问题。
## Decision-LWE
>除了Search-LWE问题外，还有一个Decision-LWE问题，该问题并不是格中的CVP问题了，而是SVP问题。接下来需要具体介绍一下Decision-LWE的问题形式，以及其为什么是格中的SVP问题。
+ `Decision-LWE`问题是`LWE`问题的另一种形式，其中文翻译过来被叫做`判定LWE问题`。
# Search—LWE具体题型
## LWE的搜索问题
## MLWE的搜索问题
## RLWE的搜索问题
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 iyheart的博客！
wechat