学到矩阵的运算课程进度已经过了三分之一了,但是到线性空间这块只听和做点小笔记,但是还没怎么刷题。由于矩阵运算线性代数有上过现在采取边复习线性空间的内容,边刷题,边看矩阵运算的内容,边写矩阵运算的相关练习题目。
等学习到多项式,估计LSFR的学习就可以提上日程了QAQ,原本大二下就想学习LFSR,可是看了BM算法自己根本理解不了,估计还是数学知识积累的不够,还是打基础吧。
目前已经学习了三种线性空间:
- 几何空间是线性空间
- 有序数组(也就是向量)是线性空间
- Ms×n(K)是线性空间
回顾——矩阵的秩
矩阵的基本运算
矩阵加法与数量乘法
定义1:矩阵记号、相等、零矩阵
(1)Ms×n(K)={数域K上s×n矩阵},当s=n时,记为Mn(K),也就是方阵。
(2)两个矩阵相等⟺这两个矩阵行数相等,列数相等对应元素相等。
(3)元素全为0
定义2:矩阵加法
⎣⎢⎢⎡a11⋮as1...⋱…a1n⋮asn⎦⎥⎥⎤+⎣⎢⎢⎡b11⋮bs1...⋱…b1n⋮bsn⎦⎥⎥⎤=⎣⎢⎢⎡a11+b11⋮as1+bs1...⋱…a1n+b1n⋮asn+bsn⎦⎥⎥⎤
定义3:矩阵的数量乘法
k⎣⎢⎢⎡a11⋮as1...⋱…a1n⋮asn⎦⎥⎥⎤=⎣⎢⎢⎡ka11⋮kas1...⋱…ka1n⋮kasn⎦⎥⎥⎤
矩阵乘法
先来看看矩阵乘法的引入,矩阵乘法的引入还是比较重要的,当时在学线代的时候对于矩阵乘法完全就是死记,一点也不知道规律在哪里。
首先矩阵的乘法是从映射的乘法引出的,考虑这么一个问题:平面上原点O,以及平面上一点P其坐标为(x,y),OP构成一个长度为r的有向线段即OP,并且OP与x轴夹角为α。有一个转角为θ的旋转记作σ,其中σ是一个映射。求旋转之后P′的坐标,如下图所示:
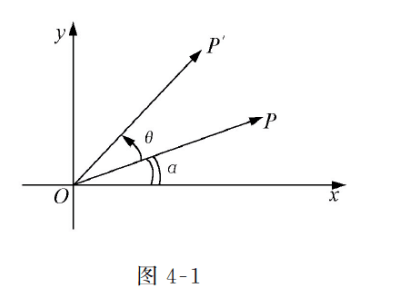
- 首先我们由于旋转前后
r是不变的量,所以先将OP的坐标使用参数方程的形式表示出来。
{x=rcosαy=rsinα
- 之后我们可以通过不变的量
r,将OP的坐标也使用参数方程的形式表示出来,将OP的参数方程带入就可以得到一个关于x、y与x'、y'的关系
{x′=rcos(α+θ)=rcosαcosθ−rsinαsinθy′=rsin(α+θ)=rsinαcosθ+rcosαsinθ⇒{x′=xcosθ−ysinθy′=xcosθ+ysinθ
- 将
x、y当做未知数,将sin、cos当做系数,就会得到一个系数矩阵,所以定义转角为θ的旋转σ为:
σ↦[cosθsinθ−sinθcosθ]
- 同理可以得到,一个转角为ϕ的旋转τ为:
τ↦[cosϕsinϕ−sinϕcosϕ]
接下来我们考虑先旋转θ角度,再旋转ϕ角度;也就是先进行σ映射,再进行τ映射,那么就可以得到转角为(θ+ϕ),如下图所示。
- 同上面的方式,我们就可以比较轻松的得到映射乘法的结果:
τ∘σ↦[cos(θ+ϕ)sin(θ+ϕ)−sin(θ+ϕ)cos(θ+ϕ)]
- 记A=[cosϕsinϕ−sinϕcosϕ],[cosθsinθ−sinθcosθ],根据映射的乘法就导出了矩阵的乘法
AB:=τ∘σ↦[cos(θ+ϕ)sin(θ+ϕ)−sin(θ+ϕ)cos(θ+ϕ)]
- 将A、B带入并且将乘法的结果矩阵里面的三角函数使用和角公式展开就得到如下所示的乘法式子,可以发现规律:
- (先看左边矩阵的第一行和右边矩阵的第1、2列)左边矩阵的第一行第一个元素与右边矩阵第一列的一个元素相乘加上左边矩阵第一行第二个元素与右边矩阵第一列第二个元素相乘,组成了乘积矩阵第一行第一个元素的值。
- (先看左边矩阵的第一行和右边矩阵的第1、2列)左边矩阵的第一行第一个元素与右边矩阵第二列的一个元素相乘加上左边矩阵第一行第二个元素与右边矩阵第二列第二个元素相乘,组成了乘积矩阵第一行第二个元素的值。
- 从而发现:左边矩阵的第i行的各个元素与右边矩阵第j列各个元素相乘之和即为结果矩阵C(i,j)元
[cosϕcosϕ−sinϕsinϕ][cosϕcosϕ−sinϕsinϕ]=[cosθcosϕ−sinθsinϕsinθcosϕ+cosθsinϕ−sinθcosϕ−cosθsinϕcosθcosϕ−sinθsinϕ]
从而导出了矩阵乘法的定义
定义4:矩阵乘法
记:As×n=⎣⎢⎢⎡a11⋮as1…⋱…a1n⋮asn⎦⎥⎥⎤,Bn×m=⎣⎢⎢⎡b11⋮bn1…⋱…b1m⋮bn×m⎦⎥⎥⎤,则有
As×n∗Bn×m=⎣⎢⎢⎡a11⋮as1…⋱…a1n⋮asn⎦⎥⎥⎤∗⎣⎢⎢⎡b11⋮bn1…⋱…b1m⋮bnm⎦⎥⎥⎤:=⎣⎢⎢⎡a11b11+...+a1nbn1⋮as1b11+...+asnbn1…⋱…a11b1m+...+a1nbnm⋮as1b1m+...+asnbnm⎦⎥⎥⎤s×m
要点:
- 左矩阵的列数=右矩阵的行数
- 乘积矩阵AB(i,j)=ai1b1j+...+ainbmj=∑k=1naikbkj
- AB的行数=A的行数,AB的列数=B的列数
接下来再介绍一下矩阵乘法的一些要点,先给个例子看看
eg1:
A=[1020],B=[0001]
则有如下结果
AB=[1020][0001]=[0020]
BA=[0001][1020]=[0000]
从例题中我们可以看出,如下两个结论
结论1:矩阵相乘不满足交换律
结论2:两个非零矩阵相乘结果可能是零矩阵
eg2:通过引入矩阵的乘法,其实就可以将行向量与列向量相乘当做矩阵的乘法来运算。
有两个矩阵A=[1,…,1]1×n,B=⎣⎢⎢⎡1⋮1⎦⎥⎥⎤n×1,那么这两个矩阵相乘就会出现如下结果:
AB=[n]1×1BA=⎣⎢⎢⎡1⋮1…⋱…1⋮1⎦⎥⎥⎤n×n
通过上面两个例子有如下
定义5:
定义矩阵中数都为1的矩阵为J,即J:=⎣⎢⎢⎡1⋮1…⋱…1⋮1⎦⎥⎥⎤
性质1:矩阵乘法运算律
- (AB)C=A(BC),结合律,如果A、B、C能够相乘
- A(B+C)=AB+AC,左分配律
- (B+C)D=BD+CD
- 定义In:=⎣⎢⎢⎢⎢⎢⎢⎡10⋮0001⋮00……⋱……00⋮1000⋮01⎦⎥⎥⎥⎥⎥⎥⎤,In称为n级单位矩阵,则有As×nIn=As×n,IsAs×n=As×n。特别地:若A是n级矩阵,则IA=AI=A
性质2:矩阵乘法与数乘
- k(AB)=(kA)B=A(kB)
矩阵的幂
定义1:矩阵的幂
Am:=A...A。一共m个A相乘,m∈N∗。
A0:=I
容易得到:
- Ak⋅Al=Ak+l,其中k,l∈N
- (Ak)l=Akl,其中k,l∈N
矩阵的转置
性质:矩阵的转置与矩阵乘积的转置
- (A+B)′=A′+B′
- (kA)′=kA′
- (AB)′=B′A′
乘积矩阵的秩
定理1:
设矩阵A,B二者可以相乘,那么就有rank(AB)≤min{rank(A),rank(B)}
引入与证明如下:
特殊矩阵
基本矩阵
基本矩阵的定义:
形如如下的矩阵都被称为基本矩阵,矩阵这个数表中只有一个元素是1,其余元素都是0,使用Eij来表示,其中i=1,...,s;j=1,...,n:
Eij:=⎣⎢⎢⎢⎢⎢⎡0000000000……⋱……001ij0000000⎦⎥⎥⎥⎥⎥⎤s×n
定理1:任意矩阵使用基本矩阵表示
任取A∈Ms×n(K),则有如下
A=⎣⎢⎢⎡a11⋮as1…⋱…a1n⋮asn⎦⎥⎥⎤=⎣⎢⎢⎡a11⋮0…⋱…0⋮0⎦⎥⎥⎤+...+⎣⎢⎢⎡0⋮0…⋱…a1n⋮0⎦⎥⎥⎤+...+⎣⎢⎢⎡0⋮as1…⋱…0⋮0⎦⎥⎥⎤+...+⎣⎢⎢⎡0⋮0…⋱…0⋮asn⎦⎥⎥⎤
那么就有:A=a11E11+...+a1nE1n+...+as1Es1+...+asnEsn
定理2:基本矩阵构成一个基与对应的维数
设k11E11+...+k1nE1n+...+ks1Es1+...+ksnEsn=0,则有⎣⎢⎢⎡k11⋮ks1...⋱…k1n⋮ksn⎦⎥⎥⎤=0。
从而得到k11=...=k1n=...=ks1=...=ksn=0。
于是就有E11,...,E1n,E21,...,E2n,Es1,...,Esn线性无关,因此E11,...,E1n,E21,...,E2n,Es1,...,Esn是Ms×n(K)的一个基。
因此 dim Ms×n(K)=sn,特别地 dim Mn(K)=n2
对角矩阵
对角矩阵的定义:
主对角线以外的元素全为0的方阵称为对角矩阵,简记作diag{d1,d2,...,dn},形如如下的矩阵:
⎣⎢⎢⎢⎡d10000d200……⋱…00dn−10000dn⎦⎥⎥⎥⎤
定理1:
数量矩阵
上、下三角矩阵
初等矩阵
可逆矩阵
练习
矩阵的基本运算练习
4-1典型例题1-5


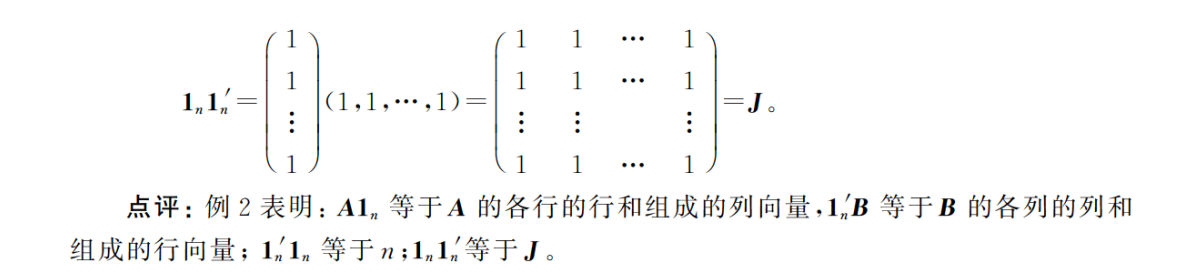


4-1典型例题6-10



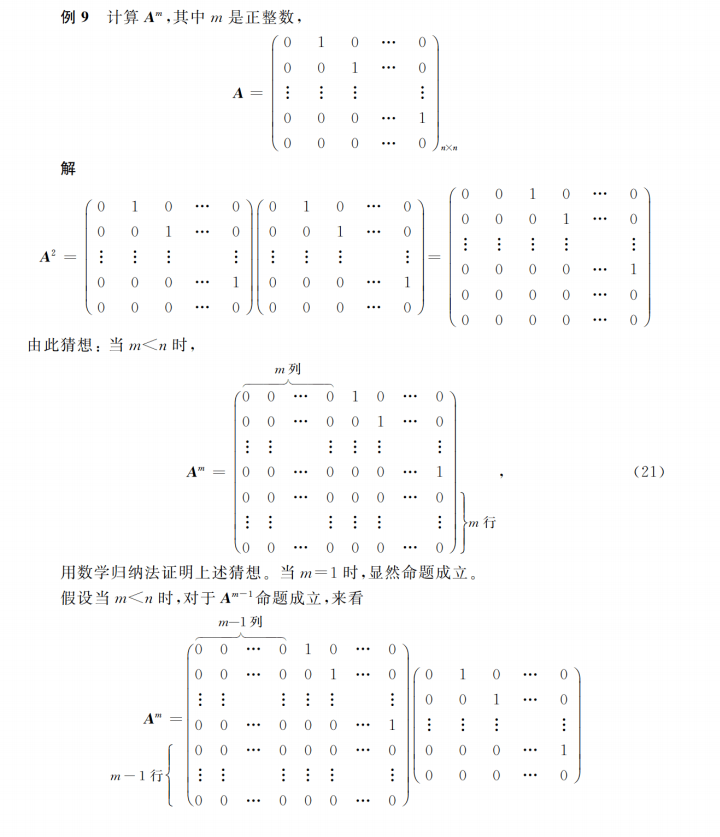


4-1典型例题11-12



4-1习题
















