题目描述如下:
将其翻译后如下:
在定义一个格或者谈论格在密码学中出现的作用之前,先来复习一下线性代数与基相关的知识。
下面的挑战应该被视为复习,如果下面的知识对你来说是全新的,你可能需要做一些背景阅读。
通常,我们推荐Hoffstein, Pipher, Silverman所写的《An Introduction to Mathematical Cryptography》这本书,以及这个pdf文档和他们的应用Wayback Machine
下面进入复习阶段:
一个在域F F F V \mathbf{V} V v ∈ V v\in V v ∈ V a ∈ F a\in F a ∈ F
对于向量的加法:v + w = z v+w=z v + w = z v , w , z ∈ V v,w,z\in V v , w , z ∈ V
对于数量乘法,是域F F F a ∗ v = w a*v=w a ∗ v = w v , w ∈ V , a ∈ F v,w\in V,a\in F v , w ∈ V , a ∈ F
你可能第一次见到向量是在二维向量空间中,以及实数域定义的。我们也将用二维向量空间以及实数域来举一个例子:
考虑一个二维的向量空间:v ∈ V v\in V v ∈ V v = ( a , b ) v=(a,b) v = ( a , b ) a , b ∈ R a,b\in R a , b ∈ R
该二维向量空间的加法为:( a , b ) + ( c , d ) = ( a + c , b + d ) (a,b)+(c,d)=(a+c,b+d) ( a , b ) + ( c , d ) = ( a + c , b + d )
该二维向量空间的数乘运算为:c ∗ v = c ∗ ( a , b ) = ( c a , c b ) c*\mathbf{v}=c*(a,b)=(ca,cb) c ∗ v = c ∗ ( a , b ) = ( c a , c b )
除了向量的加法与数乘运算之外,还定义了内积(也称为点积),也就是两个向量相乘结果返回一个数。如下所示:
v ⋅ w = a \mathbf{v·w}=a v ⋅ w = a v , w ∈ V , a ∈ F v,w\in V,a\in F v , w ∈ V , a ∈ F 在二维空间中的例子就为:v ⋅ w = ( a , b ) ⋅ ( c , d ) = a c + b d v·w=(a,b)·(c,d)=ac+bd v ⋅ w = ( a , b ) ⋅ ( c , d ) = a c + b d
接下来做一题,该题是实数域下的三维向量空间中向量的加法、数乘、内积混合运算,题目如下,flag为计算出的结果没有东西包裹:
v = ( 2 , 6 , 3 ) , w = ( 1 , 0 , 0 ) , u = ( 7 , 7 , 2 ) 3 ∗ ( 2 ∗ v − w ) ⋅ 2 ∗ u = ? v=(2,6,3),w=(1,0,0),u=(7,7,2)\\
3*(2*v-w)·2*u=?
v = ( 2 , 6 , 3 ) , w = ( 1 , 0 , 0 ) , u = ( 7 , 7 , 2 ) 3 ∗ ( 2 ∗ v − w ) ⋅ 2 ∗ u = ?
6 ∗ [ ( 4 , 12 , 6 ) − ( 1 , 0 , 0 ) ] ⋅ ( 7 , 7 , 2 ) = 6 ∗ ( 3 , 12 , 6 ) ⋅ ( 7 , 7 , 2 ) = 6 ∗ ( 3 ∗ 7 + 12 ∗ 7 + 6 ∗ 2 ) = 6 ∗ 117 = 702 \begin{array}{l}
6*[(4,12,6)-(1,0,0)]·(7,7,2)\\
= 6*(3,12,6)·(7,7,2) \\
= 6*(3*7+12*7+6*2) \\
= 6*117\\
=702
\end{array}
6 ∗ [ ( 4 , 1 2 , 6 ) − ( 1 , 0 , 0 ) ] ⋅ ( 7 , 7 , 2 ) = 6 ∗ ( 3 , 1 2 , 6 ) ⋅ ( 7 , 7 , 2 ) = 6 ∗ ( 3 ∗ 7 + 1 2 ∗ 7 + 6 ∗ 2 ) = 6 ∗ 1 1 7 = 7 0 2
题目描述如下:
翻译过来如下:
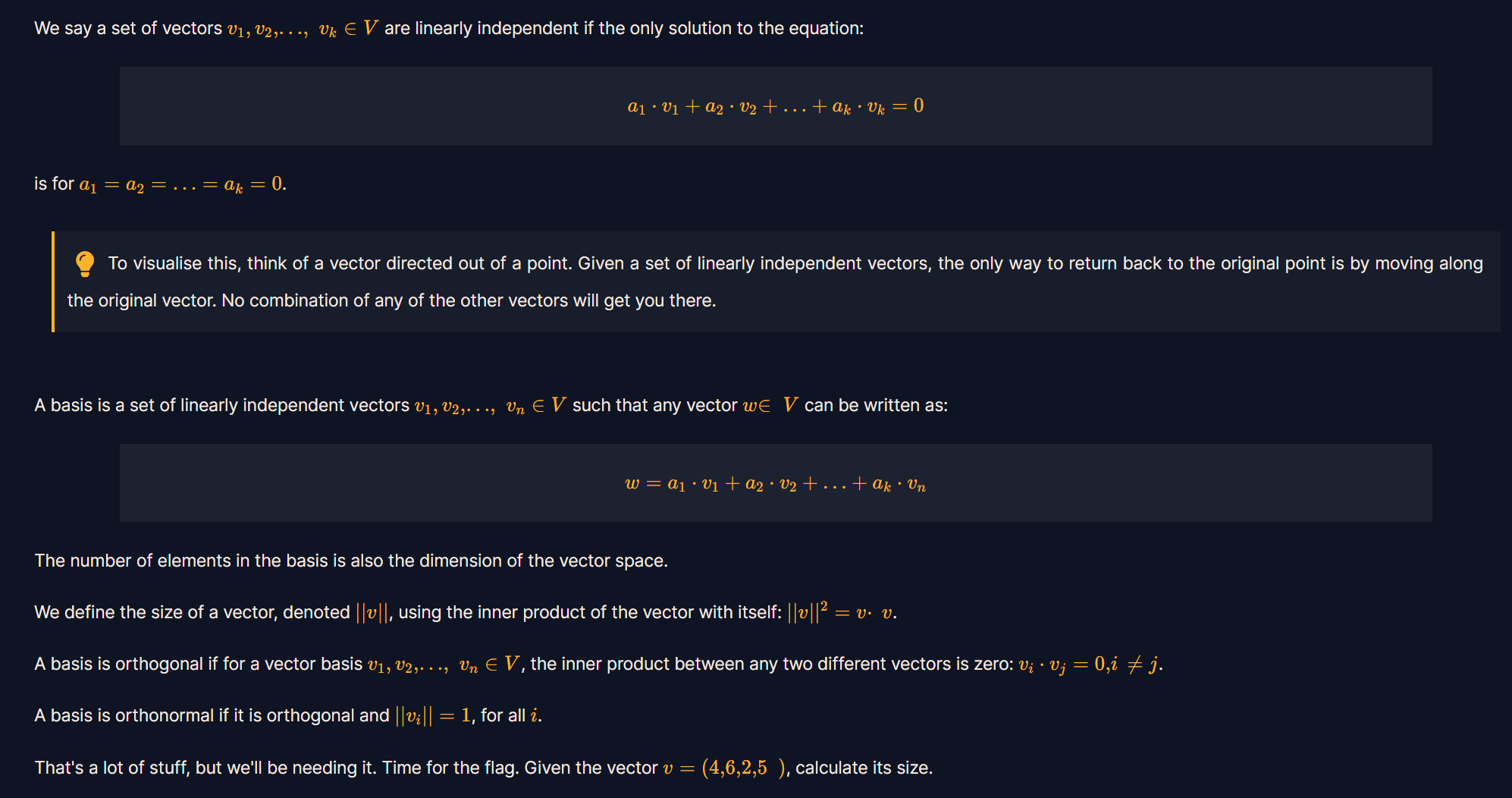
我们说一个向量集合v 1 , v 2 , . . . , v k ∈ V v_1,v_2,...,v_k\in V v 1 , v 2 , . . . , v k ∈ V a 1 v 1 + a 2 v 2 + . . . + a k v k = 0 a_1\mathbf{v_1}+a_2\mathbf{v_2}+...+a_k\mathbf{v_k}=\mathbf{0} a 1 v 1 + a 2 v 2 + . . . + a k v k = 0 a 1 = a 2 = . . . = a k = 0 a_1=a_2=...=a_k=0 a 1 = a 2 = . . . = a k = 0
为了更直观体现,想象一个向量从一个点出发。给定一组线性无关的向量,返回原点的唯一方法是沿原向量移动。其他向量不论经过多少加法运算和数乘运算都不会回到这个点。
向量空间的基就是一组线性无关向量的集合v 1 , v 2 , . . . , v n ∈ V v_1,v_2,...,v_n\in V v 1 , v 2 , . . . , v n ∈ V w ∈ V w\in V w ∈ V
w = a 1 v 1 + a 2 v 2 + . . . + a k v n w = a_1\mathbf{v_1}+a_2\mathbf{v_2}+...+a_k\mathbf{v_n}
w = a 1 v 1 + a 2 v 2 + . . . + a k v n
向量空间的基中向量的个数也就是线性空间的维数,记作d i m V dim~V d i m V
我们定义向量的一个大小,记为∣ ∣ v ∣ ∣ ||v|| ∣ ∣ v ∣ ∣ ∣ ∣ v ∣ ∣ 2 = v ⋅ v ||v||^{2}=v·v ∣ ∣ v ∣ ∣ 2 = v ⋅ v
对于向量空间的一个基v 1 , v 2 , . . . , v n ∈ V v_1,v_2,...,v_n\in~V v 1 , v 2 , . . . , v n ∈ V v i ⋅ v j = 0 , i ≠ j v_i·v_j=0,i≠j v i ⋅ v j = 0 , i = j 正交基
对于一个正交基来说,所有基向量∣ ∣ v i ∣ ∣ = 1 ||v_i||=1 ∣ ∣ v i ∣ ∣ = 1
接下来就是本题的尝试:
计算向量v = ( 4 , 6 , 2 , 5 ) v=(4,6,2,5) v = ( 4 , 6 , 2 , 5 )
∣ ∣ v ∣ ∣ 2 = v ⋅ v = ( 4 , 6 , 2 , 5 ) ⋅ ( 4 , 6 , 2 , 5 ) = 16 + 36 + 4 + 25 = 16 + 4 + 36 + 25 = 20 + 36 + 25 = 20 + 61 = 81 \begin{array}{l}
||v||^{2}\\
=v·v
\\=(4,6,2,5)·(4,6,2,5)
\\=16+36+4+25
\\=16+4+36+25
\\=20+36+25
\\=20+61
\\=81
\end{array}
∣ ∣ v ∣ ∣ 2 = v ⋅ v = ( 4 , 6 , 2 , 5 ) ⋅ ( 4 , 6 , 2 , 5 ) = 1 6 + 3 6 + 4 + 2 5 = 1 6 + 4 + 3 6 + 2 5 = 2 0 + 3 6 + 2 5 = 2 0 + 6 1 = 8 1
本题是介绍斯密特正交化,也就是将一个给定的基(可能是正交基,可能不是正交基),将该基转化成一个正交基。如果需要转化成单位正交基,还需要对该正交基进行归一化处理。
题目描述如下:
翻译过来就如下所示:
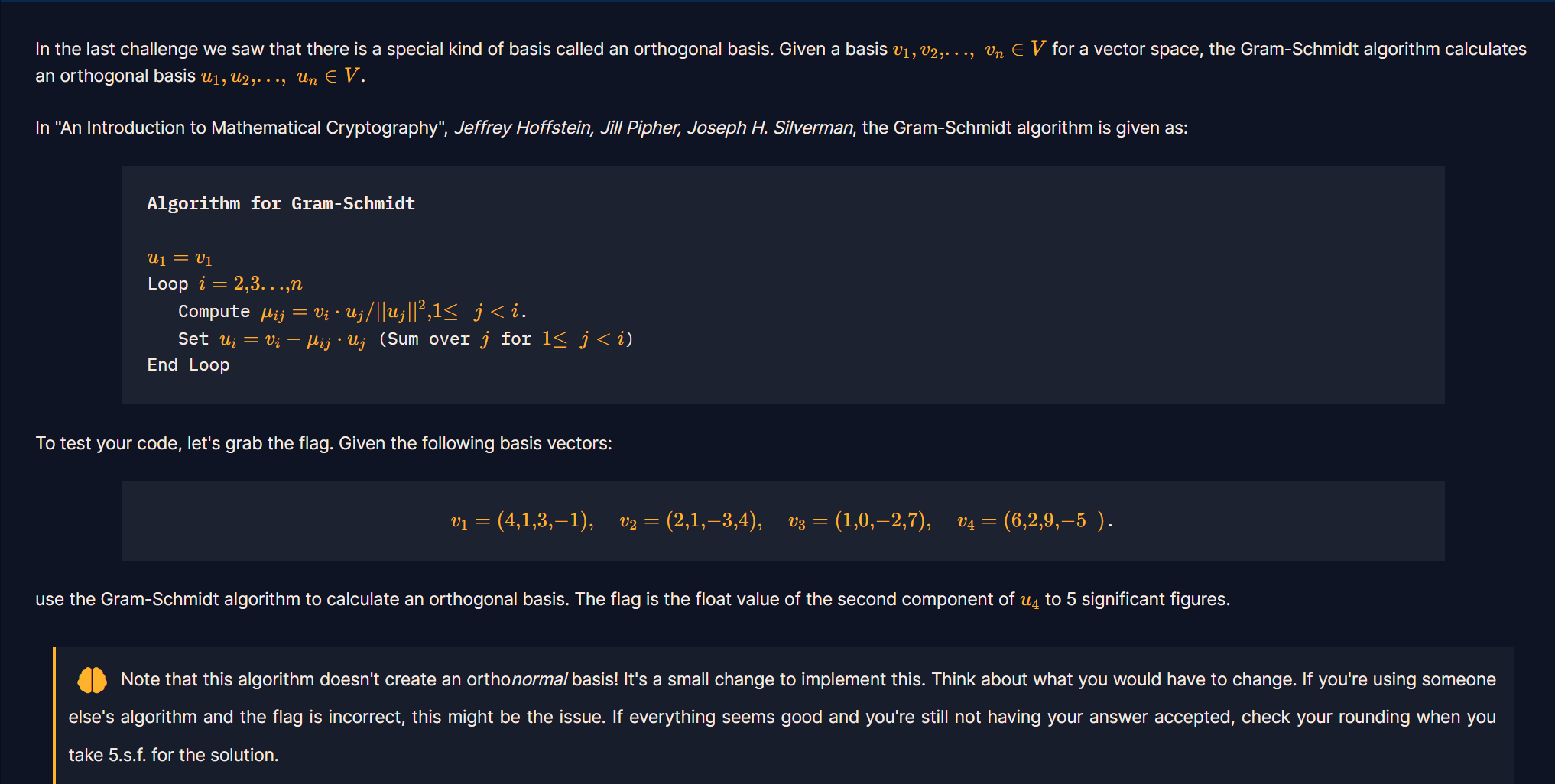
在上一个挑战中,我们了解到了一个被称为正交基 的一个特别的基。给出向量空间中一个基v 1 , v 2 , . . . , v n ∈ V v_1,v_2,...,v_n\in V v 1 , v 2 , . . . , v n ∈ V u 1 , u 2 , . . . , u n ∈ V u_1,u_2,...,u_n \in V u 1 , u 2 , . . . , u n ∈ V
在Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman所写的书《An Introduction to Mathematical Cryptography》,斯密特正交化算法的伪代码如下所示:
u 1 = v 1 L o o p i = 2 , 3 , . . . , n C o m p u t e μ i j = v i ⋅ u j ∣ ∣ u i ∣ ∣ 2 , 1 ≤ j < i . S e t u i = v i − μ i j ⋅ u j ( S u m o v e r j f o r 1 ≤ j < i ) E n d L o o p \begin{array}{l}
u_1=v_1\\
Loop~i=2,3,...,n\\
~~~~~~Compute~\mu_{ij}=\frac{v_i·u_j}{||u_i||^{2}},1≤j<i.\\
~~~~~~Set~u_i=v_i-\mu_{ij}·u_{j}~(Sum~over~j~for~1≤j<i)\\
End~Loop
\end{array}
u 1 = v 1 L o o p i = 2 , 3 , . . . , n C o m p u t e μ i j = ∣ ∣ u i ∣ ∣ 2 v i ⋅ u j , 1 ≤ j < i . S e t u i = v i − μ i j ⋅ u j ( S u m o v e r j f o r 1 ≤ j < i ) E n d L o o p
接下来就是根据伪代码编写一个斯密特正交化的代码,并计算下面这个基的正交基,flag的值是u 4 u_4 u 4
v 1 = ( 4 , 1 , 3 , − 1 ) v 2 = ( 2 , 1 , − 3 , 4 ) v 3 = ( 1 , 0 , − 2 , 7 ) v 4 = ( 6 , 2 , 9 , − 5 ) v_1=(4,1,3,-1)~~~v_2=(2,1,-3,4)~~~v_3=(1,0,-2,7)~~v_4=(6,2,9,-5)
v 1 = ( 4 , 1 , 3 , − 1 ) v 2 = ( 2 , 1 , − 3 , 4 ) v 3 = ( 1 , 0 , − 2 , 7 ) v 4 = ( 6 , 2 , 9 , − 5 )
注意:这个算法不能创造一个正交基。但是如果要创建一个正交基只需要做一个很小的改动,想想需要改动什么。如果你使用的是别人的算法,如果flag是错误的,这个错误点就是问题的所在。但是如果算法没有问题,flag仍然错误,尝试一下四舍五入。
编写如下算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 def vec_multi (u1:list ,v1:list ): """ :param u1: 进行内积的向量之一 :param v1: 进行内积的向量之一 :return: 内积的结果,float或int类型 """ result = 0 length = len (u1) assert length == len (v1) for i in range (length): result += u1[i]*v1[i] return result def vec_add (u1:list ,v1:list ): """ :param u1: 进行向量加法的其中一个向量 :param v1: 进行向量加法的其中一个向量 :return: vec:list: 向量加法的结果 """ result = [] length = len (u1) assert length == len (v1) for i in range (length): result.append(u1[i]+v1[i]) return result def vec_sub (u1:list ,v1:list ): """ :param u1: 被减向量 :param v1: 减向量 :return: vec:list: 向量减法的结果 """ result = [] length = len (u1) assert length == len (v1) for i in range (length): result.append(u1[i]-v1[i]) return result def vec_times (k:int or float ,u1 ): """ :param k: 数乘的值 :param u1: 数乘向量 :return: vec: 返回结果向量 """ result = [] for i in range (len (u1)): result.append(k*u1[i]) return result def Gram_Schmidt (vec:list ): """ 该函数实现的是斯密特正交化 :param vec: 传入的是一个基,并且是一个列表类型,两个行向量v1 = (1,2),v2 = (3,4);则传入[[1,2],[3,4]],列向量就转置成行向量再传入 :return: vec2 : 经过斯密特正交化后的一个正交基 """ vec2 = [] vec2.append(vec[0 ]) for i in range (1 ,len (vec)): mu_list = [] for j in range (i): mu = vec_multi(vec[i],vec2[j])/vec_multi(vec2[j],vec2[j]) mu_list.append(mu) temp = vec_sub(vec[i], vec_times(mu_list[0 ], vec2[0 ])) for k in range (1 ,len (vec2)): temp = vec_sub(temp,vec_times(mu_list[k],vec2[k])) vec2.append(temp) return vec2 vec = [] v1 = [4 ,1 ,3 ,-1 ] v2 = [2 ,1 ,-3 ,4 ] v3 = [1 ,0 ,-2 ,7 ] v4 = [6 ,2 ,9 ,-5 ] vec.append(v1) vec.append(v2) vec.append(v3) vec.append(v4) result = Gram_Schmidt(vec) print (result)""" [[4, 1, 3, -1], [2.5925925925925926, 1.1481481481481481, -2.5555555555555554, 3.851851851851852], [-0.7229219143576828, -1.0201511335012596, 2.012594458438287, 2.1259445843828715], [-0.3619189659458126, 0.916107382550335, 0.21488938603032665, 0.11309967685806738]] 得到的结果是:0.916107382550335,保留五位有效数字就为:0.91611 """
本题正式介绍格,题目描述如下:
翻译过来就如下:
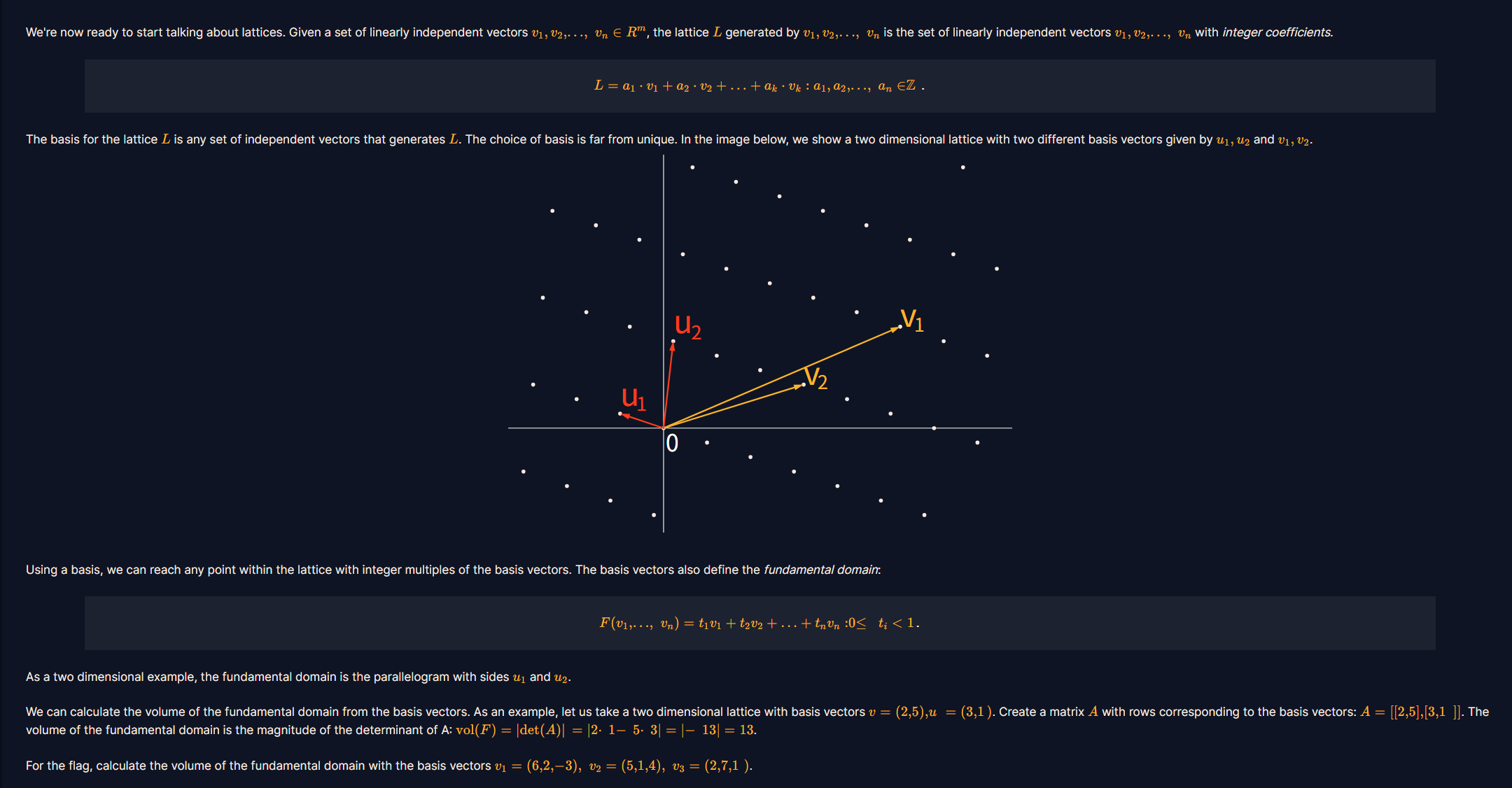
我们现在准备开始讨论格。有一个线性无关向量组v 1 , v 2 , . . . , v n ∈ R m v_1,v_2,...,v_n\in ~R^{m} v 1 , v 2 , . . . , v n ∈ R m L L L v 1 , v 2 , . . . , v n v_1,v_2,...,v_n v 1 , v 2 , . . . , v n
L = a 1 ⋅ v 1 + a 2 ⋅ v 2 + . . . + a k ⋅ v k : a 1 , a 2 , . . . , a n ∈ Z L = a_1·v_1+a_2·v_2+...+a_k·v_k:a_1,a_2,...,a_n\in \Z
L = a 1 ⋅ v 1 + a 2 ⋅ v 2 + . . . + a k ⋅ v k : a 1 , a 2 , . . . , a n ∈ Z
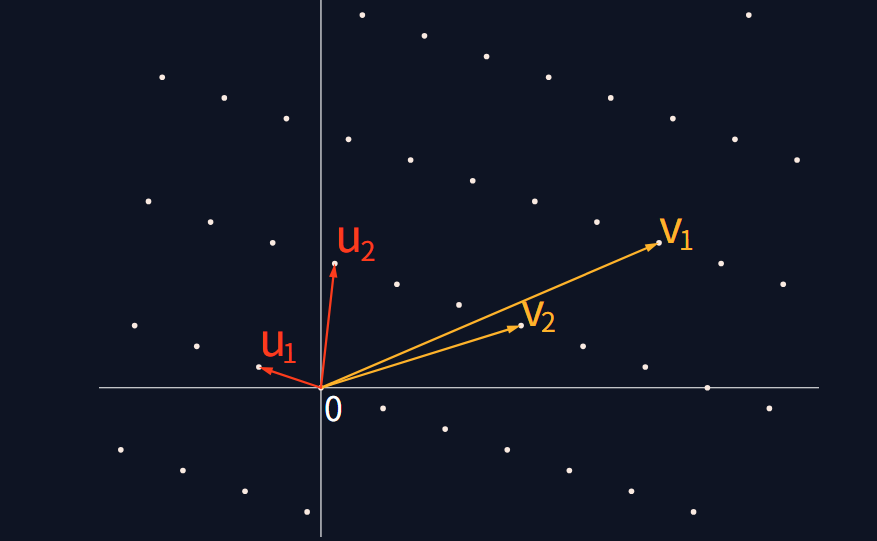
格L L L L L L u 1 、 u 2 u_1、u_2 u 1 、 u 2 v 1 、 v 2 v_1、v_2 v 1 、 v 2
使用一个基,我们能通过基向量的整数倍,到达格中的任一一点,基向量还定义了基本域,基本域定义如下:
F ( v 1 , . . . , v n ) = t 1 v 1 + t 2 v 2 + . . . + t n v n : 0 ≤ t i < 1 F(v_1,...,v_n)=t_1v_1+t_2v_2+...+t_nv_n:0≤t_i<1
F ( v 1 , . . . , v n ) = t 1 v 1 + t 2 v 2 + . . . + t n v n : 0 ≤ t i < 1
还是以二维几何空间为例子,二维平面中格的基本域就是以基向量u 1 、 u 2 u_1、u_2 u 1 、 u 2
我们可以通过格的基向量,计算基本域的体积。仍然使用二维几何空间为例子,有基向量v = ( 2 , 5 ) v=(2,5) v = ( 2 , 5 ) u = ( 3 , 1 ) u=(3,1) u = ( 3 , 1 ) A=\pmatrix{2&5\\3&1} ,从而这个基本域的体积为矩阵A A A
v o l ( F ) = ∣ d e t ( A ) ∣ = ∣ ∣ 2 ∗ 1 − 5 ∗ 3 ∣ ∣ = ∣ ∣ 2 − 15 ∣ ∣ = 13 vol(F)=|det(A)|=||2*1-5*3||=||2-15||=13
v o l ( F ) = ∣ d e t ( A ) ∣ = ∣ ∣ 2 ∗ 1 − 5 ∗ 3 ∣ ∣ = ∣ ∣ 2 − 1 5 ∣ ∣ = 1 3
对于本题的flag,就是计算一个格基本域的体积,给出格基v 1 = ( 6 , 2 , − 3 ) , v 2 = ( 5 , 1 , 4 ) , v 3 = ( 2 , 7 , 1 ) v_1=(6,2,-3),v_2=(5,1,4),v_3=(2,7,1) v 1 = ( 6 , 2 , − 3 ) , v 2 = ( 5 , 1 , 4 ) , v 3 = ( 2 , 7 , 1 )
e该基构成了一个矩阵A = [ 6 2 − 3 5 1 4 2 7 1 ] A=\begin{bmatrix}6 & 2& -3\\5 & 1 &4\\2 & 7 & 1\end{bmatrix} A = ⎣ ⎢ ⎡ 6 5 2 2 1 7 − 3 4 1 ⎦ ⎥ ⎤
v o l ( F ) = ∣ ∣ d e t ( A ) ∣ ∣ = ∣ ∣ 6 ∗ 1 ∗ 1 + 2 ∗ 4 ∗ 2 + ( − 3 ) ∗ 5 ∗ 7 − ( − 3 ) ∗ 1 ∗ 2 − 6 ∗ 4 ∗ 7 − 1 ∗ 5 ∗ 2 ∣ ∣ = ∣ ∣ 6 + 16 − 105 + 6 − 168 − 10 ∣ ∣ = ∣ ∣ 22 − 99 − 178 ∣ ∣ = 255 \begin{array}{l}
vol(F)\\=||det(A)||\\=||6*1*1+2*4*2+(-3)*5*7-(-3)*1*2-6*4*7-1*5*2||\\=||6+16-105+6-168-10||
\\=||22-99-178||
\\=255
\end{array}
v o l ( F ) = ∣ ∣ d e t ( A ) ∣ ∣ = ∣ ∣ 6 ∗ 1 ∗ 1 + 2 ∗ 4 ∗ 2 + ( − 3 ) ∗ 5 ∗ 7 − ( − 3 ) ∗ 1 ∗ 2 − 6 ∗ 4 ∗ 7 − 1 ∗ 5 ∗ 2 ∣ ∣ = ∣ ∣ 6 + 1 6 − 1 0 5 + 6 − 1 6 8 − 1 0 ∣ ∣ = ∣ ∣ 2 2 − 9 9 − 1 7 8 ∣ ∣ = 2 5 5
题目描述如下:
翻译过来如下:
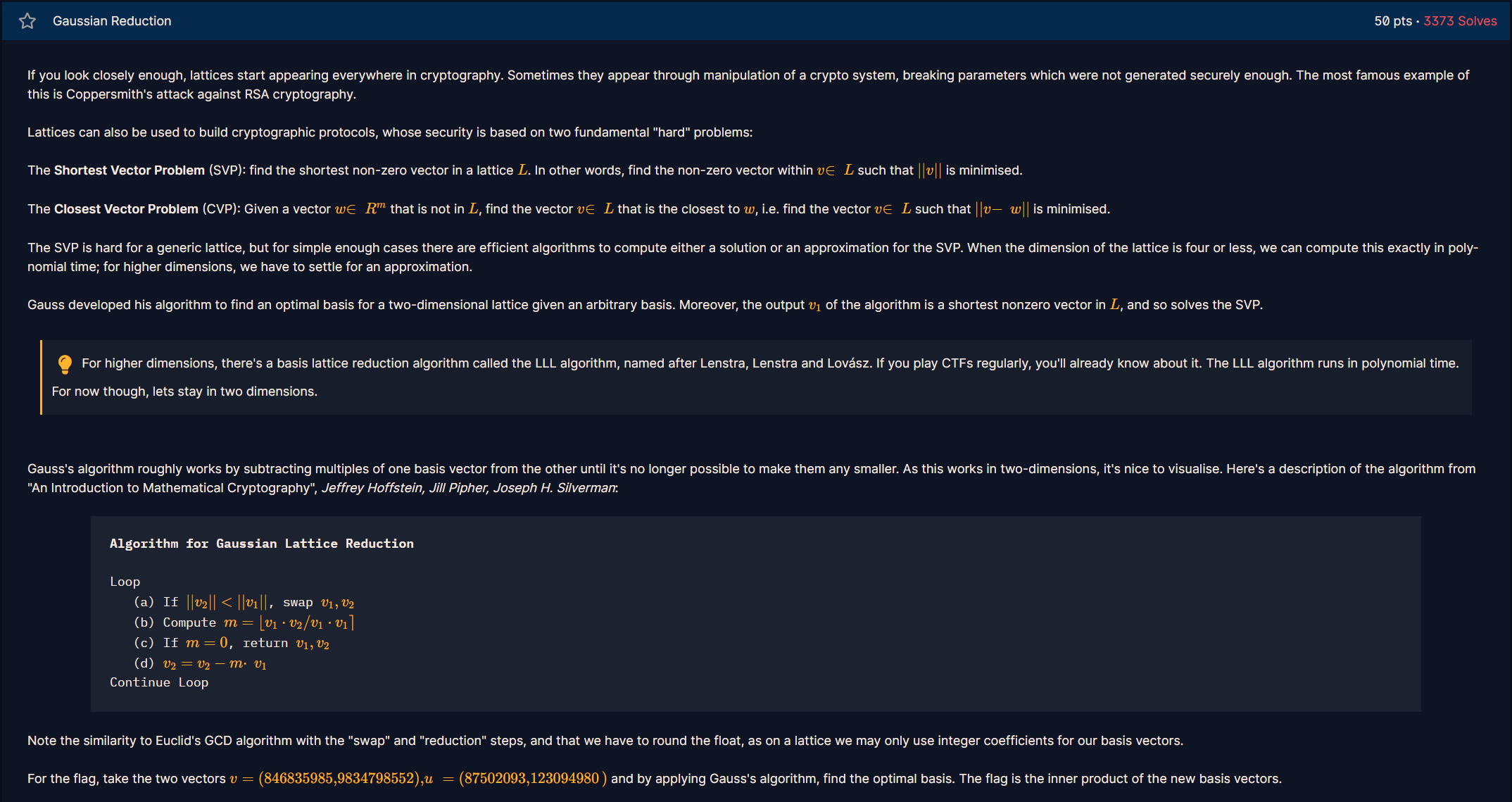
如果你仔细观察,格在密码学中无处不在。有时他们通过某个密码系统通过代数操作显现出来的,用来攻破那些没有被安全地生成的参数。最著名的例子就是Coppersmith针对RSA的攻击。
格也通过两个基本的格困难问题,也可以用来建造密码学协议,这两个基本的格困难问题如下:
最短向量问题(SVP):找到格L L L v ∈ L v\in L v ∈ L ∣ ∣ v ∣ ∣ ||v|| ∣ ∣ v ∣ ∣
最近向量问题(CVP):有一个不在格上的向量w ∈ R m w\in R^{m} w ∈ R m w w w v ∈ L v\in L v ∈ L ∣ ∣ v − w ∣ ∣ ||v-w|| ∣ ∣ v − w ∣ ∣
SVP对于通用格来说是比较困难的,但是对于足够简单的情况,有高效的算法能够计算SVP的解或者近似解。当格的维数为四或更小时,我们可以在多项式时间内精确计算出最短向量。但是对于更高维度的格,我们只能得到其近似值。
高斯发明了一个算法,该算法是用于二维格,给定任意一个格基,寻找二维格中的最优基,此外该算法输出结果中的向量v 1 v_1 v 1 L L L
对于高维格来说,有一种格基规约算法该算法被称为LLL算法,它是以Lenstra、Lenstra、 Lovász这三个人名字的首字母命名的。如果你经常玩CTF,那你已经早就知道它了。LLL算法运行在多项式时间内。不过现在我们依然在二维空间中讨论问题。
高斯算法大致通过从一个基向量的倍数中减去另一个向量,直到无法让基向量变小。由于这个算法用于二维空间的,所以该算法是很容易可视化的。下面这个伪代码是高斯算法的具体过程,来源于Jeffrey Hoffstein、Jill Pipher、Joseph H. Silverman写的这本《An Introduction to Mathematical Cryptography》
L o o p ( a ) I f ∣ ∣ v 2 ∣ ∣ < ∣ ∣ v 1 ∣ ∣ , s w a p v 1 , v 2 ( b ) C o m p u t e m = ⌊ v 1 ⋅ v 2 v 1 ⋅ v 1 ⌉ ( c ) I f m = 0 , r e t u r n v 1 , v 2 ( d ) v 2 = v 2 − m ⋅ v 1 C o n t i n u e L o o p \begin{array}{l}
Loop\\
~~~~(a) If ||v_2||<||v_1||,swap~v_1,v_2 \\
~~~~(b) Compute~m=⌊\frac{v_1⋅v_2}{v_1·v_1}⌉ \\
~~~~(c) If~~~m=0, return~v_1,v_2 \\
~~~~(d) v_2=v_2-m·v_1\\
Continue Loop
\end{array}
L o o p ( a ) I f ∣ ∣ v 2 ∣ ∣ < ∣ ∣ v 1 ∣ ∣ , s w a p v 1 , v 2 ( b ) C o m p u t e m = ⌊ v 1 ⋅ v 1 v 1 ⋅ v 2 ⌉ ( c ) I f m = 0 , r e t u r n v 1 , v 2 ( d ) v 2 = v 2 − m ⋅ v 1 C o n t i n u e L o o p
注意:高斯算法与欧几里得的GCD算法中swap和reduction步骤有比较相似的地方,并且我们必须对浮点数进行四舍五入,因为格上我们只能使用整数系数作为基向量。
本题的flag是,使用高斯算法找到两个向量v = ( 846835985 , 9834798552 ) , u = ( 87502093 , 123094980 ) v=(846835985,9834798552),u=(87502093,123094980) v = ( 8 4 6 8 3 5 9 8 5 , 9 8 3 4 7 9 8 5 5 2 ) , u = ( 8 7 5 0 2 0 9 3 , 1 2 3 0 9 4 9 8 0 )
编写如下算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 def vec_multi (u1:list ,v1:list ): """ :param u1: 进行内积的向量之一 :param v1: 进行内积的向量之一 :return: 内积的结果,float或int类型 """ result = 0 length = len (u1) assert length == len (v1) for i in range (length): result += u1[i]*v1[i] return result def vec_sub (u1:list ,v1:list ): """ :param u1: 被减向量 :param v1: 减向量 :return: vec:list: 向量减法的结果 """ result = [] length = len (u1) assert length == len (v1) for i in range (length): result.append(u1[i]-v1[i]) return result def vec_times (k:int or float ,u1 ): """ :param k: 数乘的值 :param u1: 数乘向量 :return: vec: 返回结果向量 """ result = [] for i in range (len (u1)): result.append(k*u1[i]) return result def Gaussian_reduction (v1:list ,v2:list ): """ 使用高斯规约法计算出给定二维格的最短向量 :param basis: 传入的是一个基,v1=[1,2],v2=[3,4] :return: 返回(v1,v2)大致形式如下:([1,1],[0,1]) """ if vec_multi(v2,v2) < vec_multi(v1,v1): v1,v2 = v2,v1 m = int (vec_multi(v1,v2)/vec_multi(v1,v1)) while m: v2 = vec_sub(v2,vec_times(m,v1)) if vec_multi(v2, v2) < vec_multi(v1, v1): v1, v2 = v2, v1 m = int (vec_multi(v1, v2) / vec_multi(v1, v1)) return v1,v2 v1 = [846835985 ,9834798552 ] v2 = [87502093 ,123094980 ] v1,v2 = Gaussian_reduction(v1,v2) print (v1)print (v2)print (vec_multi(v1,v2))""" [87502093, 123094980] [-4053281223, 2941479672] 7410790865146821 """
题目描述如下:
翻译如下:
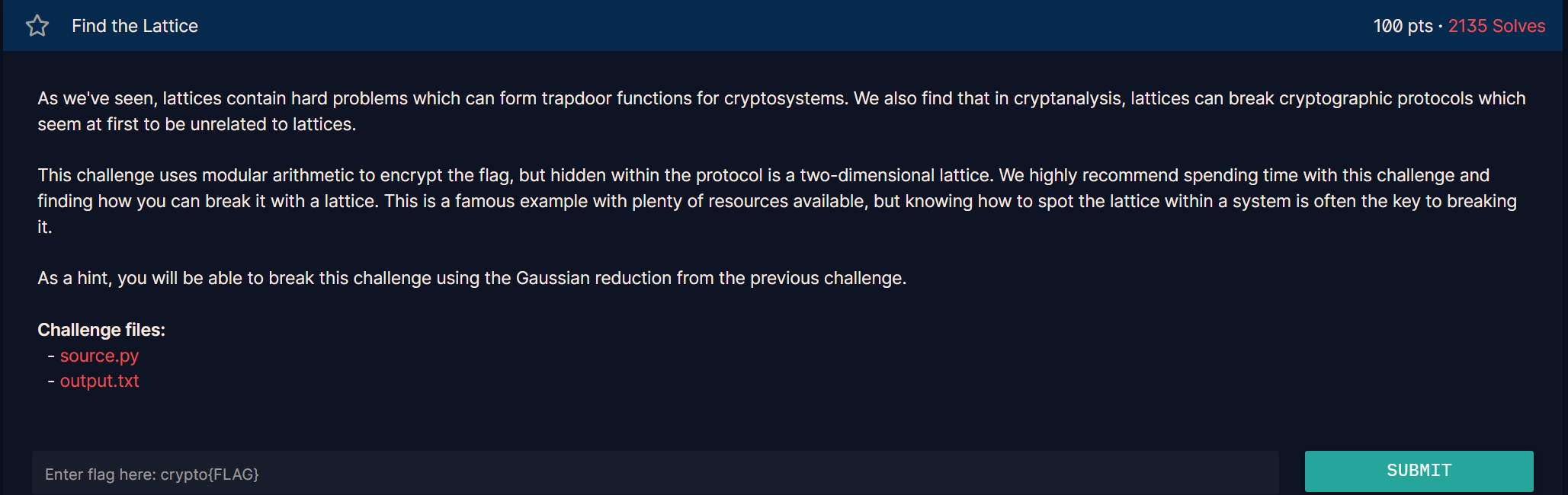
正如我们所见,格中的困难问题能在密码系统中构成一个门限函数。我们也发现在密码分析学中,格能攻击那些一开始看起来与格无关的密码学协议。
这个挑战使用模运算去加密flag,但是在这个协议中隐藏了一个二维的格。我们非常推荐花时间在这个挑战中以及你使用格能怎样破解它。
这题是一个非常著名的例子,关于它的资料非常丰富,但是在一个密码系统中找到隐藏的格经常是破解该密码系统的一个关键。
接下来就是一个带附件的题目了,先来看看该附件的source.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 from Crypto.Util.number import getPrime, inverse, bytes_to_longimport randomimport mathFLAG = b'crypto{?????????????????????}' def gen_key (): q = getPrime(512 ) upper_bound = int (math.sqrt(q // 2 )) lower_bound = int (math.sqrt(q // 4 )) f = random.randint(2 , upper_bound) while True : g = random.randint(lower_bound, upper_bound) if math.gcd(f, g) == 1 : break h = (inverse(f, q)*g) % q return (q, h), (f, g) def encrypt (q, h, m ): assert m < int (math.sqrt(q // 2 )) r = random.randint(2 , int (math.sqrt(q // 2 ))) e = (r*h + m) % q return e def decrypt (q, h, f, g, e ): a = (f*e) % q m = (a*inverse(f, g)) % g return m public, private = gen_key() q, h = public f, g = private m = bytes_to_long(FLAG) e = encrypt(q, h, m) print (f'Public key: {(q,h)} ' )print (f'Encrypted Flag: {e} ' )
题目描述如下:
翻译如下:
我非常喜欢这个密码系统,我把它放背包中并且随身携带它。为了减轻负担,我确保背包的密度不会太高。
题目描述如下:
翻译过来就为:
在开始这部分之前,你应该至少完成"格"上面格部分。
通过CryptoHack中RSA章节部分,使用LLL算法进行格基规约已经证明了是一个非常强有力的密码分析学工具。它在SVP和CVP或BDD问题中找到一个短向量表现是非常出色的。
然而,对于LWE的格基规约算法仅仅使用在某一个点。通过使格的维数或者误差变大,或者提供一个大的或混淆的基底,格基规约将不再返回格中的最短向量。这就是使得LWE称为密码学中的困难问题的原因。
哪一个计算机科学和数学家在2005年提出了LWE问题?本题的flag的值就是该科学家的名字。
来源:the_two_faces_of_lattices_in_cryptology.pdf
题目描述如下:
翻译过来为:
LWE指的是一个计算问题,在已知大量带噪声的样本的情况下,去学习一个在线性环上取值的线性函数f ( A ) f(\mathbf{A}) f ( A )
这些样本看起来像这样的一对( A , < A , S > + e ) (\mathbf{A},<\mathbf{A,S}>+e) ( A , < A , S > + e ) S \mathbf{S} S e \mathbf{e} e 小噪声误差项,而A \mathbf{A} A < A , S > <\mathbf{A,S}> < A , S > A \mathbf{A} A S \mathbf{S} S
基于LWE的密码系统种类非常多,但是他们通常由以下几个特征:
它们在两个不同的模数下进行模算数,一个是明文模数,另一个是密文模数。
密钥是模n的某个向量空间中的元素。
消息的加密方式是:将编码后的带噪声消息加入到一个大的点积结果中。
带噪声的消息,是将原消息与一个小的误差(或噪声)项适当编码后得到的和。
这个点积是密钥与向量空间的一个随机元素之间的点积,而这个随机元素会作为密文的一部分提供。
这样就像( A , < A , S > + e n c o d e d ( m , e ) ) (\mathbf{A},<\mathbf{A,S}>+encoded(m,e)) ( A , < A , S > + e n c o d e d ( m , e ) )
如果密钥已知,那么就可以将点积消去,只剩下编码后的消息与噪声。由于消息与噪声采用了特殊的编码方式,噪声可以从编码中被去除,从而只留下原始消息。
在LWE系统中,有两种常见的方法来存放消息与噪声:要么把消息存放在LWE样本的高位,把噪声放在低位,要么反过来存放。
将一些消息存放在高位的LWE加密方案例子包括Regev09和BFV
将消息存放在低位的LWE加密方案的一个例子是BGV
如果没有加入误差,哪种算法可以在多项式时间内从这些线性方程组中恢复消息。本题的flag就是该算法的名称
题目描述如下:
翻译过来如下:
现在我们将手动解密一个示例LWE系统中的消息,这个消息被隐藏在高位中。
该LWE加密系统参数如下:
一个n维的向量空间
密文模数q
明文模数p(需要满足加密的消息m < p)
缩放因子Δ ≈ q p \Delta≈\frac{q}{p} Δ ≈ p q
密钥:
密钥S \mathbf{S} S Z p n \Z^{n}_p Z p n
密文:
密文是由一对( A , b ) (\mathbf{A},b) ( A , b ) A \mathbf{A} A Z q n Z^{n}_q Z q n b b b Z q Z_q Z q
加密消息m:
样本A \mathbf{A} A Z q n Z^{n}_q Z q n
对误差项e e e [ − Δ 2 , Δ 2 ] [-\frac{\Delta}{2},\frac{\Delta}{2}] [ − 2 Δ , 2 Δ ]
计算b = < A , S > + Δ ⋅ m + e b=<\mathbf{A,S}>+\Delta·m+e b = < A , S > + Δ ⋅ m + e < A , S > <A,S> < A , S >
返回( A , b ) (\mathbf{A},b) ( A , b )
解密消息( A , b ) (\mathbf{A},b) ( A , b )
计算x = b − < A , S > m o d ( q ) x=b-<\mathbf{A,S}>~mod(~q) x = b − < A , S > m o d ( q ) x x x q意义下的值)
计算m = r o u n d ( x Δ ) m=round(\frac{x}{\Delta}) m = r o u n d ( Δ x )
返回m
在这个系统中,解密之所以可行,是因为在去掉掩码< A , S > <\mathbf{A,S}> < A , S > Δ ⋅ m + e \Delta·m+e Δ ⋅ m + e q而发生回绕。
因此,可以通过对整数除法进行四舍五入来去除误差项e e e Δ ⋅ m + e < q 2 \Delta·m+e<\frac{q}{2} Δ ⋅ m + e < 2 q
接下来给出与本次挑战相关的代码文件和密文,代码如下,flag为m的值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 n = 64 p = 257 q = 0x10001 error_bound = int (floor((q/p)/2 )) delta = int (round (q/p)) V = VectorSpace(GF(q), n) S = V.random_element() print ("S = " , S, "\n" )m = ? A = V.random_element() error = randint(-error_bound, error_bound) b = A * S + m * delta + error print ("A = " , A)print ("b = " , b)
其实本题考察的就是上面的加密和解密过程,只不过要注意的是< A , S > <A,S> < A , S >
1 2 3 4 5 6 7 8 9 10 11 12 13 14 S = (55542 , 19411 , 34770 , 6739 , 63198 , 63821 , 5900 , 32164 , 51223 , 38979 , 24459 , 10936 , 17256 , 20215 , 35814 , 42905 , 53656 , 17000 , 1834 , 51682 , 43780 , 22391 , 33012 , 61667 , 37447 , 16404 , 58991 , 61772 , 44888 , 43199 , 32039 , 26885 , 17206 , 62186 , 58387 , 57048 , 38393 , 29306 , 58001 , 57199 , 33472 , 56572 , 53429 , 62593 , 14134 , 40522 , 25106 , 34325 , 37646 , 43688 , 14259 , 24197 , 33427 , 43977 , 18322 , 38877 , 55093 , 12466 , 16869 , 25413 , 54773 , 59532 , 62694 , 13948 ) A = (13759 , 12750 , 38163 , 63722 , 39130 , 22935 , 58866 , 48803 , 15933 , 64995 , 60517 , 64302 , 42432 , 32000 , 22058 , 58123 , 53993 , 33790 , 35783 , 61333 , 53431 , 43016 , 60795 , 25781 , 28091 , 11212 , 64592 , 11385 , 24690 , 40658 , 35307 , 63583 , 60365 , 60359 , 32568 , 35417 , 22078 , 38207 , 16331 , 53636 , 28734 , 30436 , 18170 , 15939 , 966 , 48519 , 41621 , 36371 , 41836 , 4026 , 33536 , 57062 , 52428 , 59850 , 476 , 43354 , 61614 , 32243 , 42518 , 19733 , 63464 , 29357 , 56039 , 15013 ) b = 44007 s = 0 for i in range (len (S)): s += A[i]*S[i] print (s)p = 257 q = 0x10001 x = int ((b - s) % q) print (result)delta = int (round (q/p)) print (int (round (x/delta)))
题目描述如下:
翻译过来如下:
现在我们将手动解密一个示例LWE系统中的消息,这个LWE加密系统的消息被藏在低位,而噪声被藏在高位。
参数如下:
n维向量空间
密文模数q
明文模数p(需要满足加密消息m<q)
必须满足两个模数p,q互质
密钥如下:
密钥S S S Z q n \Z^{n}_q Z q n
密文形式:
密文对为( A , b ) (A,b) ( A , b ) Z q n \Z^{n}_q Z q n b b b Z q Z_q Z q
加密m的过程:
样本A为Z q n Z^{n}_q Z q n
错误样本e e e [ − q 2 p , q 2 p ] [-\frac{q}{2p},\frac{q}{2p}] [ − 2 p q , 2 p q ]
计算b = < A , S > + m + p ⋅ e b=<\mathbf{A,S}>+m+p·e b = < A , S > + m + p ⋅ e < A , S > <A,S> < A , S >
返回密文对( A , b ) (A,b) ( A , b )
解密( A , b ) (A,b) ( A , b )
计算x = b − < A , S > x=b-<A,S> x = b − < A , S > q q q x x x ( − q 2 , q 2 ] (-\frac{q}{2},\frac{q}{2}] ( − 2 q , 2 q ] [ 0 , q − 1 ] [0,q-1] [ 0 , q − 1 ]
计算m = x m o d ( p ) m=x~mod(~p) m = x m o d ( p )
在这个系统中,解密之所以可行,因为在去掉掩码< A , S > <A,S> < A , S > m + p ⋅ e m+p·e m + p ⋅ e m + p ⋅ e < q 2 m+p·e<\frac{q}{2} m + p ⋅ e < 2 q
下面有两个附件,请求出m。附件如下:
题目描述如下:
翻译过来如下:
现在来看一个公钥密码系统,通过使用LWE的加法同态性质。给定一个加密数字m的密文< A , b > <\mathbf{A,b}> < A , b > m + m 2 m+m_2 m + m 2 m 2 m_2 m 2
具体来说,对于低位消息(高噪声),可以计算:< A , b + m 2 > <\mathbf{A,b+m_2}> < A , b + m 2 >
对于高位消息(低噪声),可以计算:< A , b + Δ ⋅ m 2 > <\mathbf{A,b+\Delta·m_2}> < A , b + Δ ⋅ m 2 >
虽然当消息存储在低位时,加法同态性质更容易看出来,但当消息存储在高位时,这种性质同样存在
同样地,将两个LWE密文相加会产生一个新的有效密文,它加密的是对应明文之和。私钥持有者可以利用这一性质,通过公开许多不同的零加密来将LWE构建成一个公钥系统。为了加密,Alice首先从这些零加密中随机选择一个子集并将它们相加。根据第二条加法同态性质,这仍然是一个有效的零加密。接着,Alice对她的消息m进行新的编码,并将该编码后的消息加到这个新的零加密上。根据第一条加法同态性质,这就是一个有效的m的加密。
该过程要求对噪声项的采样分布进行精心选择,以确保最终的误差项在(高概率下)低于可成功解密所需的阈值。
为了保证安全性,攻击这必须难以判断某个LWE密文是由哪些公钥中的零加密相加得到的。为了达到这一点,公钥中零加密的数量必须显著大于LWE的维度。因此,公钥的大小为随着O ( n 2 l o g ( q ) ) O(n^{2}log(q)) O ( n 2 l o g ( q ) )
问题: Kyber1024使用的公钥大小是多少bytes?flag的值为字节数。通过上面可得知公钥大小会比1024大。
答案:
题目描述如下:
翻译如下:
噪声项的加入使得学习变成了带误差的学习。如果没有误差,你能够学得多少呢?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 from utils import listenerfrom sage.all import *FLAG = b"crypto{????????????????????????}" n = 64 p = 257 q = 0x10001 V = VectorSpace(GF(q), n) S = V.random_element() def encrypt (m ): A = V.random_element() b = A * S + m return A, b class Challenge : def __init__ (self ): self.before_input = "Would you like to encrypt your own message, or see an encryption of a character in the flag?\n" def challenge (self, your_input ): if 'option' not in your_input: return {'error' : 'You must specify an option' } if your_input['option' ] == 'get_flag' : if "index" not in your_input: return {"error" : "You must provide an index" } self.exit = True index = int (your_input["index" ]) if index < 0 or index >= len (FLAG) : return {"error" : f"index must be between 0 and {len (FLAG) - 1 } " } self.exit = True A, b = encrypt(FLAG[index]) return {"A" : str (list (A)), "b" : str (int (b))} elif your_input['option' ] == 'encrypt' : if "message" not in your_input: return {"error" : "You must provide a message" } self.exit = True message = int (your_input["message" ]) if message < 0 or message >= p: return {"error" : f"message must be between 0 and {p - 1 } " } self.exit = True A, b = encrypt(message) return {"A" : str (list (A)), "b" : str (int (b))} return {'error' : 'Unknown action' } import builtins; builtins.Challenge = Challenge listener.start_server(port=13411 )