RSA加密原理

• 感觉自己写的RSA密码分析还是比较杂，而且还有很多没有补充完整的，思来想去还是把从头开始把每个东西都完善一下。我之前打算的分类是每个RSA攻击方式，在正常RSA加密、多幂RSA加密、多素数RSA加密、对偶RSA加密、共素数RSA加密等都分析一遍。
• 但是这样的分类还是有点乱，最终决定依然按照《Cryptanalysis of RSA and Its Variants (M. Jason Hinek)》这本书的分类来进行分类。（之后如果有时间，再根据我上面的想法分个类。）
• 这篇博客正式开始我的RSA加密的密码分析学的学习，之前一直想写这个博客，但是由于基础知识有限以及时间关系一直就鸽了，现在基础知识跟上来了，直接开始疯狂学习。
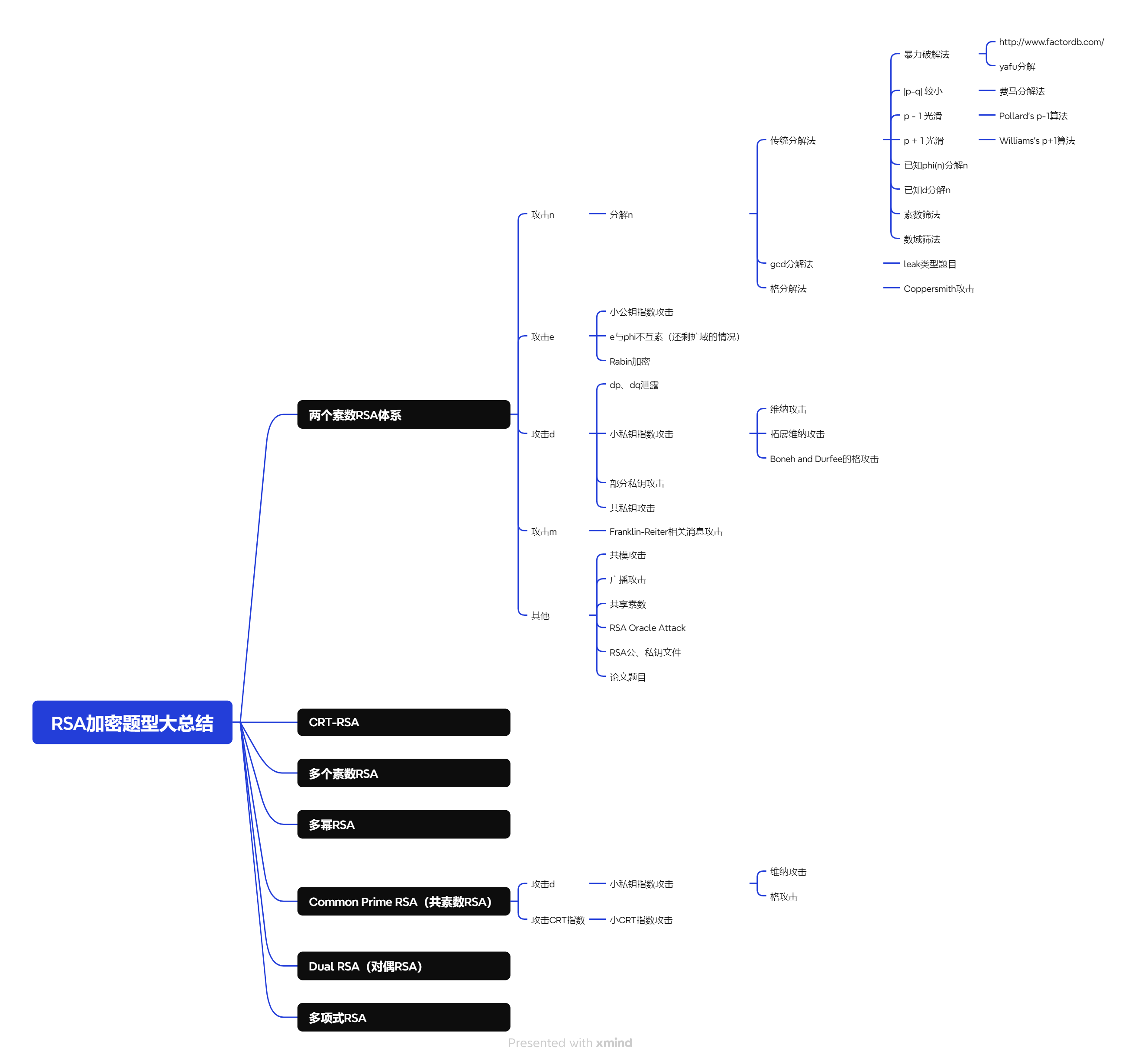
• 之前也做过不少RSA加密的题型，所以我根据集合的划分，将RSA加密题型进行分类，尽我所能的将题型分类成如下图所示，我会根据我的分类进行学习。目前还没分类完成，只能说边学边分类吧（此图会不定期跟新与完善）。这个分类的构建有参考这本国外书籍：《Cryptanalysis of RSA and Its Variants (M. Jason Hinek)》

公钥密码学

• 公钥密码学这个概念在1970年~1980年之间流行起来的，这个概念是被Diffie、Hellman、Merkle这三个人提出的。如果想要了解公钥密码学的起源，可以参考Diffie所写的The first ten years of public-key cryptography。
• 基于Douglas R. Stinson（道格拉斯·R·斯廷森），对于密码系统的定义，我们在公钥密码学中使用下面的定义：
  • 公钥密码学五元组$(P,C,K,E,D)$
  • $P$是明文的有限集合
  • $C$是密文的有限集合
  • $K$是密钥的有限集合，被称为密钥空间。
  • $E$是加密映射的有限集合，所有的公钥加密算法都属于这个集合
  • $D$是解密映射的有限集合，所有的公钥解密算法都属于这个集合
  • 对于每一个密钥$k\in K$，有一个加密规则（其实也就是一个映射）$enc_K\in E$，并且对应着有一个正确的解密规则（也可以理解为一个映射）$dec_K \in D$。
    • 对于每一个加密映射$enc_K: P\rightarrow C$和解密映射$dec_K: C\rightarrow P$，这两个函数有$dec_K(enc_K(m))=m,m\in P$
    • 对于每一个密钥$k \in K$以及每一个明文$m \in P$，$enc_K(m)$和$dec_K(enc_K(m))$都非常容易计算。
    • 对于几乎所有$k \in K$来说，任何与$dec_K$等价且可有效计算的算法，都在计算上不能仅有$enc_K$（这是一个映射）推导得到。也就是说，在不知道$dec_K$的情况下，解密是困难的。
    • 加密规则$enc_K$是公开的而解密规则$dec_K$是非公开的。
• 其实换一种角度思考公钥密码系统，从另一种角度看，一个公钥密码系统包含了三个有效的可计算的算法：
  • 密钥生成算法：该算法定义了密钥空间$K$
  • 加密算法和解密算法：这两个算法共同定义了明文空间$P$和密文空间$C$

RSA加密原理

• RSA加密体制是第一个被公开发表的公钥密码体制。RSA密码提示最早由Gardner在1977年于《Scientific Amrican》上发表的一篇文章中介绍。其完整的研究论文则于次年1998年由发明者Rivest、Shamir和Adleman发表，这三位作者都隶属于麻省理工学院，该密码体制最初被称为MIT公钥密码体制。

• 接下来以非专业的术语大致讲解一下RSA加密和解密过程：

  • 定义：要加密的明文为$m$，加密后得到的密文为$c$
  • 前提准备1：先选取两个素数$p、q$，计算这两个素数的乘积$n=p*q$
  • 前提准备2：计算$n$的欧拉函数，$\phi(n)=(p-1)*(q-1)$
  • 公钥的生成：生成一个公钥$e$，要求$1<e<\phi(n)$，且$e$为整数，还需要满足$gcd(e,\phi(n))=1$（也就是两者互素）
  • 私钥的生成：确定私钥$d$，私钥需要满足$e*d\equiv1~mod~(~\phi(n)~)$
  • 加密算法如下：

  $$c = m^e~mod~(~n)$$

  • 解密算法如下：

  $$m = c^d~mod(~n)$$

  • 解密正确性验证：
    • 通过欧拉定理以及欧拉函数可以将原本计算量比较大的指数运算转换为求解逆元的运算。如果稍微了解一下求解逆元的过程，其实就知道求逆元的过程本质上就是解不定方程，还需要用上欧几里得算法。
    • 由$e*d\equiv1~mod(~\phi(n))$就可以得到：$e*d=1+k*\phi(n)$
    • 所以$c^d\equiv (m^{e})^{d}\equiv m^{ed}~mod(n)$
    • 通过代换就可以得到$c^d\equiv m^{ed}\equiv m^{k*\phi(n)+1}~mod(n)$
    • 通过欧拉定理有$a^{\phi(n)}\equiv 1~mod(~n),gcd(a,n)=1$
    • 最后得到$c^d \equiv m^{ed} \equiv m^{k*\phi(n)+1}\equiv m^{k*\phi(n)}*m\equiv m~mod(~n)$
  • $(n,e)$为公钥对，$(p,q,d)$为私钥对

• 接下来使用比较专业的术语再描述一下RSA公钥加密体制的具体算法：

  • 定义明文空间与密文空间：生成两个大素数$p、q$，让$N = pq$，$P=C=Z_N$（即明文空间和密文空间就是整数模N的集合，其实就是$[0,n-1]$这个范围内的整数集）

  • 定义密钥空间：$K = \{(N,p,q,e,d):ed\equiv 1~mod(~\phi(N))\}$，其中$\phi(N)=(p-1)(q-1)$是欧拉函数。

  • 定义加密、解密规则：

    • 对于每个密钥$k\in K,k=(N,p,q,e,d)$。
    • 有加密规则$enc_K:Z_N\rightarrow Z_N$，满足算法$enc_K(x)=x^{e}~mod(~N)$。
    • 有解密规则$dec_K:Z_N\rightarrow Z_N$，满足算法$dec_K(y)=y^d~mod(~N)$

  • 其中$x,y\in Z_N$，$(e,N)$这一对被称为RSA公钥，$(d,p,q)$这个三元组被称为RSA私钥。

  • 加密函数$enc_K(x)=x^e~mod(~N)$，其中$N$是不能在一定时间内分解出来，并且满足$gcd(e,\phi(N))=1$。这个加密函数就被叫做RSA function（RSA函数）或者RSA primitive（RSA基本式）

  • $N=pq$被叫做RSA modulus（RSA模数），两个素数$p、q$被叫做RSA primes（RSA素数）

  • $e$被叫做public exponent（公钥指数）或者encrypting exponent（加密指数）

  • d被叫做private exponent（私钥指数）或者decrypting exponent（解密指数）

  • 由于公私钥指数必须满足$ed\equiv 1~mod(~\phi(N)~)$，所以有$ed=1+k\phi(N)$其中k是小整数（相比p、q、n来说），而$ed=1+k\phi(N)$这个等式就被称为RSA key equation（RSA密钥等式，简称密钥等式）

  • 解密规则正确性：

    • 对于与$N$互素的元素$a$，由欧拉定理可以得到$a^{\phi(N)}\equiv 1~(mod~N)$
    • 给定公钥$(e,N)$，以及一个明文消息$m\in Z_N,gcd(m,N)=1$，计算得到密文$c=m^e~mod(~N)$
    • 使用解密规则，并且用上欧拉定理与密钥等式有：

    \begin{align} c^d~(mod~N) &\equiv (m^e)^d~mod(~N)\\ &\equiv m^{ed} ~mod(~N)\\ &\equiv m^{1+k\phi(N)} ~mod(~N)\\ &\equiv m*(m^{\phi(N)})^k~mod(~N)\\ &\equiv m ~mod(~N) \end{align}

    • 由于$m \in Z_N$，所以$c^d\equiv m~mod(~N)$可以直接用等号连接$c^d = m~mod(N)$

  • 除此之外$gcd(m,N)>1$这种情况应该尽量避免，因为在$gcd(m,N)>1$这一情况下使用RSA加密计算出密文$c$后，$c$一定会满足$gcd(c,N)=p$或者$gcd(c,N)=q$

RSA加密进一步理解