格密码入门

造格解线性方程

• 当一个多元线性方程有一个比较小的解，那么就有可能可以使用基于格的启发式方法进行求解。这种方法的思路就是，在构造出的某个格中，尝试找到一个特定的最短向量。

• 我们所考虑的方法依赖于一个尚未被证明的假设，该假设涉及到格中小向量的分布或性质，因此这种方法本质上只是启发式，而非严格保证成功的算法。

• 举一个简单的例子来说明一下这个通用方法。假设我们希望求解下面的线性方程：其中$x,y,z,w\in Z$都是未知数，并且已知$x,z,w$的值比较小，而$y$可以是任意整数。

$$Ax+By+Cz=w$$

• 注意，此时我们能将这个方程，以及两个平凡方程$x=x$，$y=y$，写成一个向量-矩阵方程：$\vec{u}\mathbf{B}=\vec{v}$

$$(x,z,y) \begin{bmatrix} 1 & 0 & A\\ 0 & 1 & C\\ 0 & 0 & B \end{bmatrix}=(x,z,w)$$

• 在上述矩阵$\mathbf{B}$的各行向量是线性无关的，因此可以推出$\mathbf{B}$构成了某个格$L$的一组基，进一步就有：
  • 则就有$\vec{u}=(x,y,z)\in \Z^{3}$，而目标向量$\vec{v}=(x,y,w)$。
  • 通过展开向量-矩阵方程就可以很清晰的看到，目标向量是基矩阵的一个整数线性组合。因此，很容易证明目标向量就在这个格上。
  • 当目标向量$\vec{v}$和其反向量$-\vec{v}$是该格中唯一的最短向量时，我们只需要通过求解该格的最短向量问题，即可解出原线性方程（对于这样一个小规模的格，这个问题可以高效求解），一旦得到$\vec{v}$，就可以解出方程。
  • 进一步就可以利用$\vec{u}\mathbf{B}=\vec{v}$中的$\vec{u}$，从而恢复出$x,y,z,w$的全部数值。

总结：通过上述说明，我们已知知道了造格的要点之一：目标向量必须由基矩阵通过整数线性组合。

• 通过上面的描述，我们的非常希望目标向量$\vec{v}$是格$\mathbf{L}$中的一个最短向量。接下来一个非常关键的点就是如何判断、证明或者是严格证明目标向量$\vec{v}$是否有可能成为格$\mathbf{L}$中的最短向量。

  • 这题提供一个严格证明的方法：
    • 如果要证明某个格中的向量$\vec{v}$是最短向量，那一个非常好的证明就是类比证明$a≥b,b≥a\Leftrightarrow a=b$。
    • 估计出格中的最短向量的上界$A$，估计出格中最短向量的下界$B$，并证明$B≤\vec{v}≤A$，
    • 最后如果能证明的话尽量证明出$A=B$（可以类比证明集合相等，或者高数的夹逼准则）
  • 但是实际上可能严格证明不了，所以就给出了两个判断最短向量的标准，下面是其中一个：
    • 假设目标向量$\vec{v}$可能是格$\mathbf{L}$中的最短向量，记上面的基向量$\vec{a}=(1,0,A),\vec{b}=(0,1,C),\vec{c}=(0,0,B)$
    • 那么目标向量必须比基矩阵中所有的基向量都短，也就是让$X=max\{|x|,|y|,|z|\}$。
    • 因此目标向量就满足$||\vec{v}||≤\sqrt{3}X$，那么就有$X≤|A|,|B|,|C|$是向量$\vec{v}$是最短向量的必要条件。
  • 判断最短向量的第二个标准如下：
    • 如果$\vec{v}$是最短向量，那么该向量就必须满足闵科夫斯基界限Minkowski's bound，也就是当格的维数$dim(L)=n$，时其最短向量总满足$||\vec{v}||≤\sqrt{n}vol(L)^{\frac{1}{3}}$，其中$vol(L)=|det(B)|=|B|$，
    • 运用到这里的例子就是$||\vec{v}||≤\sqrt{3}vol(L)^{\frac{1}{3}}$
    • 再使用第一个判断标准就可以推出：$X≤|B|^{\frac{1}{3}}$，这个条件就是目标向量$\vec{v}$满足闵科夫斯基界限的一个充分条件。
    • 通常情况下，如果目标向量满足闵科夫斯基界限，那么它也会满足第一个判据所给出的界，不过在某些情况下这一点不成立，所以这两个判据应当始终加以检查。
  • 当目标向量满足上面两个判据时，我们就可以确定它有可能是该格中的一个最短向量，在这一阶段，一般来说，我们只能寄希望于它确实是最短向量，并且希望能够通过求解该格的最短向量问题将其恢复出来。特别地，在以这种方式求解线性方程时，我们将依赖下面这个假设：
    • 设矩阵$\mathbf{B}$是格$\mathbf{L}$的一个基，$\vec{v}\in L$。如果向量$\vec{v}$比矩阵$\vec{B}$中的所有基向量都短，并且满足这个格$\mathbf{L}$闵科夫斯基界限，那么$\pm\vec{v}$就是格$L$中的最短向量。
    • 当上面的这一假设对某一类格（对应于某个线性方程）成立时，用来判断目标向量是否为最短向量的两个判据所给出的界，就可以作为求解该线性方程组的方法的有效界限。
    • 结合前面给出的例子：假设$|A|\approx |B|\approx|C|$，则满足闵科夫斯基界限的向量也会比每一个基向量都要短。如果上述假设对由基矩阵$B$生成的格成立，那么我们预期只要满足：$X≤|B|^{\frac{1}{3}}$，就能就解任何具有相同形式（并且满足相同假设）的线性方程。
  • 在很多情况下，目标向量$\vec{v}$的各个分量是不平衡的。当这种情况出现的时候，就要进一步放宽上面判断方法所允许的界限。例如上述例子中，假设$X,Z,W$是$x,z,w$的界，并且假设$X>Z,W$，也就是我们认为$x$是$x,z,w$中最大的一个。这时候可以从右侧将向量-矩阵方程乘一个对角矩阵，也就是如下：
    • 对角矩阵$\mathbf{D}=\begin{bmatrix}1 & 0&0 \\0 & \frac{X}{Z} & 0 \\0 & 0& \frac{X}{W}\end{bmatrix}$，右乘该对角矩阵$\vec{u}\mathbf{B}\mathbf{D}=\vec{v}\mathbf{D}=\vec{v'}$
    • 右乘后的结果：$(x,y,z)\begin{bmatrix}1 & 0&\frac{AX}{W} \\0 & \frac{X}{Z} & \frac{CX}{W} \\0 & 0& \frac{BX}{W}\end{bmatrix}=(x,z\frac{X}{Z},w\frac{Z}{W})$
    • 右乘后就得到新的目标向量$\vec{v'}$，该向量是一个由基矩阵$\mathbf{B'}$所构成的一个新的格$\mathbf{L'}$，那么这个新的目标向量的分量就被平衡了，并且满足$||\vec{v'}||≤(X^2+(\frac{ZX}{Z})^{2}+\frac{WZ}{W})≤\sqrt{3}X$
    • 还有$vol(L')=|det(B')|=\frac{BX^{2}}{ZW}$，并且基向量的长度也会随之增大，因此未知量取值大小的界可以相应放宽，而目标向量仍然能够同时满足成为最短向量的两个判断依据。只要目标向量的各个分量是不平衡的，这种用于优化界限的方法就可以采用。
    • 在一些使用该技术的攻击描述中，这种优化会直接与初始格的构造过程融合在一起。
  • 同样的思想也可以应用到存在多于一个方程、且这些方程共享部分未知量的情形中。
    • 前面的例子中，假设我们知道$x,y$还满足方程$A'x+C'z+D=0$，其中$D$是比较小的。利用这两个方程，我们可以构造出新的向量-矩阵方程。也就是将基矩阵的中间那一列替换成新方程的参数
    • 构造后的向量-矩阵方程：$(x,z,y)\begin{bmatrix}1 & A' & A\\0 & C' & C\\0 & 0 & B\end{bmatrix}=(x,-D,w)$，构造出来后并按照前文所述的方法，继续推导相应的界，使得目标向量有可能成为该格中的一个最短向量。
    • 同样地，如果目标向量的各个分量不平衡，我们可以通过将该方程乘以一个合适的对角矩阵，来构造一个新的格以及对应的目标向量。
    • 由于需要计算格的体积来求出闵科夫斯基界限，那么向量-矩阵方程的构造应当使得矩阵的行列式能方便地计算，通常的做法就是将矩阵构造成三角矩阵。

• 前面都在说线性方程，现在来看看非线性方程，当已知一个非线性方程存在较小解时，可以对该问题进行线性化处理，从而使用上述方法来尝试求解新的问题例如：

  • 形如这样的方程：$Ax+Bx^{2}+Cz^{2}=D$的方程，
  • 可以通过令$x'=x,y'=x^2,z'=z^{2}$，将其线性化为新的方程$Ax'+By'+Cz'=D$
  • 注意：其实还存在其他方法可以直接求解非线性方程，并且在某些情况下这些方法能够给出更优解的界限。例如某些情况下的Coppersmith攻击。

造格解模线性方程

• 上面造格解线性方程这个想法，同样也可以应用到多元模线性方程中：

  • 使用相同的例子，现在我们希望找到同余式的小解：$Ax+By+Cz\equiv w~mod(~N)$，其中$N$是一些已知的整数。
  • 可以先将同余式转换为多元线性方程：$Ax+By+Cz=w+nN$，其中$n$是未知的整数。此时只是构造了一个新的线性方程（定义在整数环上），其中引入了一个新的未知量。因此我们可以直接将前面介绍的方法应用到这个新的方程中。
  • 具体来说可以构造相应的向量-矩阵形式的方程：$\vec{u}\mathbf{B}=\vec{v}$

  $$(x,y,z,-n) \begin{bmatrix} 1&0&0&A\\ 0&1&0&B\\ 0&0&1&C\\ 0&0&0&N \end{bmatrix}=(x,y,z,w)$$

  • 构造之后就可以尝试将$(x,y,z,w)$作为矩阵行生成的格中最短向量来就解。实际上，这里描述的方法可以用来说明一个广为人知的经验性理论(folklore结果)：关于如何寻找模线性方程的小解。

    • 考虑一般的多元模线性方程：$a_1x_1+...+a_nx_n\equiv 0~(~mod~N)$，这里所有的$a_i$和$N$都是已知的，并且设$X_1,...,X_n＞0$为整数，使得$|x_1|≤X_1,|x_n|≤X_n$
    • 这个经验性结论就是：当$\Pi^{n}_{i=1}X_i≤N$，未知量$x_1,...,x_n$是可以被解出的。

  • 虽然这个结论多年来一直为人所知并被广泛使用，但对其的理论解释直到2008年由Hermann和May在论文Solvinglinearequations modulo divisors: Onfactoring given any bits.才写出。接下来简述一下他们两个的结果

    • 假设$gcd(a_n,N)=1$，在论文中通过将原来的模方程两边同时乘$-a_n^{-1}~mod(~N)$，将一般的模方程转换为一个等价的模方程。从而得到$b_1x_1+...+b_{n-1}x_{n-1}\equiv x_n~mod(~N)$，其中$b_i=-a_{n}^{-1}a_i~mod(~N),i=1,...,n$
    • 再将新的线性同余方程转换为线性方程：$b_1n_1+...+b_{n-1}x_{n-1}=-x_n-nN$，其中$n$是整数
    • 根据新的线性方程，可以造出一个向量-矩阵方程

    $$(x_1,...,x_{n-1},n) \begin{bmatrix} 1&0&0&\dots&0&b_1\\ 0&1&0&\dots&0&b_2\\ \vdots&&\ddots&&\vdots&\vdots\\ 0&0&0&\dots&1&b_{n-1}\\ 0&0&0&\dots&0&N \end{bmatrix} =(x_1,...,x_{n-1},x_n)$$

    • 此时我们将这个向量-矩阵方程右乘一个对角矩阵

    $$D= \begin{bmatrix} \frac{N}{X_1}&0&0&\dots&0\\ 0&\frac{N}{X_2}&&&0\\ \vdots&&\ddots&&\vdots\\ 0&&&\frac{N}{X_{n-1}}&0\\ 0&0&\dots&0&\frac{N}{X_n} \end{bmatrix}$$

    • 此时我们的目标向量就会变成$\vec{v}=(\frac{x_1N}{X_1},...,\frac{x_{n-1}N}{X_{n-1}},\frac{x_nN}{X_n})$，此时每一个分量的界都是$N$。因此就有$||\vec{v}||≤\sqrt{n}N$
    • 右乘一个对角矩阵后得到的新格$L'$，其体积为：$vol(L')=N\Pi^{n}_{i=1}\frac{N}{X_i}=N^{n+1}\Pi^{n}_{i=1}\frac{1}{X_i}$
    • 因为该新格是n维格，因此使目标向量满足闵科夫斯基界限的一个充分条件是：$\sqrt{n}N≤\sqrt{n}(N^{n+1}\Pi^{n}_{i=1}\frac{1}{X_i})^{\frac{1}{n}}$，或者可以更简单的表述为$\Pi^{n}_{i=1}X_i≤N$，这就是我们想要得到的结果。
    • 注意：通过构造可知，目标向量作为最短向量的另一个判据预计也会满足。由于$a_n^{-1}$很可能与$N$大小相当，因此每一个基向量都将大于$N$。同时，当$X_n$明显小于$N$时，每个基向量的大小也会增大。重新标记系数和变量后，总能选择一个$X_n$，使得所有基向量都大于$\sqrt{n}N$。因此，当$\Pi^{n}_{i=1}X_i≤N$，且之前说的假设对该格成立时，该解应该是可以被找到的。

Matrix warm up

• 题目来源：tangcuxiaojkuai Matrix_warm_up | NSSCTF
• 题目附件如下：

from Crypto.Util.number import *
from random import randint
from secret import flag

p = getPrime(256)

print("p =", p)
print("c =", randint(1,p)*vector(Zmod(p), [i*getPrime(128) for i in flag]))

• 首先通过题目代码会发现，代码实现的是这样的一个过程：

  • 随机生成一个长256位的素数
  • 构造一个模p下的向量，向量的每个分量都是一个随机的128位的素数，乘上flag每个字符的ASCII码。再模上$p$
  • 最后再乘一个随机数$x$，随机数的范围为$x\in[1,p)$

• 通过查看代码，我们不妨设：256位的素数为p，128位的素数分别为$q_1,q_2,...,q_n$，flag的每个字符分别为$c_1,c_2,...,c_n$，那么代码就可以表示为这样，乘积后向量每个分量表示为$a_1,a_2,...,a_n$，随机数为$r$：

$$r(q_1c_1,q_2c_2,...,q_nc_n)\equiv (a_1,a_2,...,a_n)~mod(~p)$$

• 很显然，这样其实就有线性方同余程组：

$$\begin{cases} rq_1c_1&\equiv a_1~mod(~p)\\ rq_2c_2&\equiv a_2~mod(~p)\\ ......&\equiv ...\\ rq_nc_n&\equiv a_n~mod(~p) \end{cases} \Rightarrow \begin{cases} q_1c_1&\equiv \frac{a_1}{r}~mod(~p)\\ q_2c_2&\equiv \frac{a_2}{r}~mod(~p)\\ ......&\equiv ~......\\ q_nc_n&\equiv \frac{a_n}{r}~mod(~p) \end{cases}$$

• 接下来我们把线性同余方程组转换为线性方程组：

$$\begin{cases} q_1c_1&= \frac{a_1}{r^{-1}~mod(~p)}+k_1p\\ q_2c_2&= \frac{a_2}{r^{-1}~mod(~p)}+k_2p\\ ......&= ~......\\ q_nc_n&= \frac{a_n}{r^{-1}~mod(~p)}+k_np \end{cases}$$

• 这样我们就能构造一个向量矩阵方程，其中未知量构成向量，已知量构成矩阵（也被称为基矩阵）：
  • $\vec{v}=(k_1,k_2,...,k_n,1)$
  • $\mathbf{B}=\begin{bmatrix}p&0&...&0&0\\0&p&...&0&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\dots&p&0\\0&0&\dots&0&p\\a_1 &a_2&\dots& a_{n-1}&a_{n}\end{bmatrix}$
• 这样就有，如果向量含有$r$的倍数的话，那其实就不是最短向量了，所以我们需要将$r$提取出来，

$$\vec{v}\mathbf{B}=(rq_1c_1,rq_2c_2,...,rq_nc_n)=r(q_1c_1,q_2c_2,...,q_nc_n)$$

• 接下来我们就要先证明：$r^{-1}\vec{v}$这个向量中每个分量都是整数，这样才符合格的定义（也就是我们所构造的向量矩阵方程的结果在基矩阵所构成的这个格上），也就是我们的向量$\vec{v}$以及$r^{-1}\vec{v}$都需要是整数。首先$\vec{v}$中每个分量是整数，这个是很显然的。
  • 当$r^{-1}$是在实数域下的除法，那就会是分数，不是整数。
  • 而$r^{-1}$要是在模意义下的逆元，那就是整数，不是分数。
  • 很显然$r^{-1}$其实是在模意义下的逆元，所以$r^{-1}$是一个整数。
• 接下来我们就需要判断我们所造的格最短向量的界限如何，我们采用判断最短向量的第二个标准：
  • 如果$\vec{v}$是最短向量，那么该向量就必须满足闵科夫斯基界限，首先我们可以确定$n=40$，根据题目结果向量的长度可以确定。
  • 我们构造的矩阵是$41×40$的矩阵，但是最后一行$a_i$并不会被$p$整除，也就是线性表出不了$p$。但是会存在一个幺模矩阵$U$，使得$UB$的结果最后一行为0（也就是把最后一行消掉）
  • 从而得到结论，这个格的维数其实就是$dim(L)=40$，但是$L$的行列式并不是$\left|\begin{array}{ccc}p&0&...&0&0\\0&p&...&0&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\dots&p&0\\0&0&\dots&0&p\end{array}\right|$的结果，而是$p^{n-1}$说是最后一行使得格变得更密集。（主要可能需要注意是在$Z^{n}$中的格）
  • 接下来我们就可以计算出这个格中的闵科夫斯基界限，也就是最短向量必须满足$||\vec{c}||≤ \sqrt{40}vol(L)^{\frac{1}{40}}=x$，$x$的比特位数满足252

• 计算完闵科夫斯基界限之后，我们需要确定一下目标向量$(q_1c_1,q_2c_2,...,q_nc_n)$的长度会不会在闵科夫斯基界限范围之内。但此时我们是不知道$c_1,...c_n$的，所以我们取$c_1=...=c_n=255$。然后随机生成40个128比特的素数，粗略计算其界限。粗略计算是139远小于闵科夫斯基界限。所以我们可以由此判断，我们构造的目标向量其实就是这个格中的最短向量。

• exp如下：

from Crypto.Util.number import *
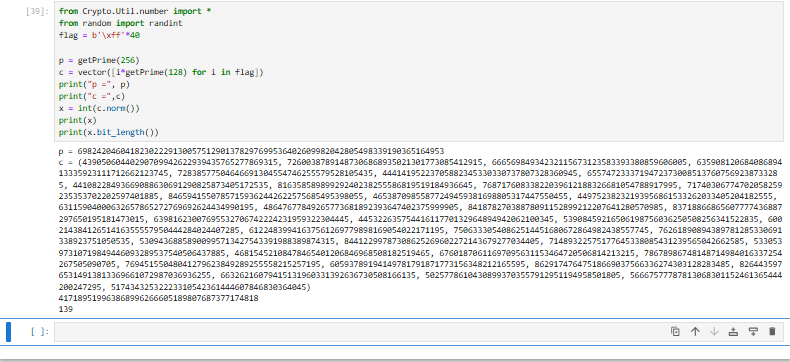
p = 98599605855990863958662823830259118267375283238963264208942746159972368798977
c = (82517335089994719678720440397443953324384116847602255948002639513101104313901, 23480188129189591225240386556937897340033310681946797651109881140283150083100, 15745298061459065444463644608757257986229810898393004395352776218436881867854, 84270435615636794052799481698023318073557231543509363804769535392387106088012, 96201177281893449383084244768818058633149464193199178668137778957874162588597, 43099159137504756238001406956750489932275012152611165794936270563202575868628, 87473505105909878544169429075138231076098232834027353502500829730748021802487, 40526868536247532569035007288241093602738034216676401111616964676485866001367, 44063716593961353493617098833905785233979061481957760044796936148478757568227, 73878801949618274670593476331042214019727738696724993431466987347899203829551, 49611915001043486900506624481468610085773333425213914365595384853737803495962, 73663397192166635927598415179372372658073408573520164162260288496381183157084, 51733741043276334909533397330697507522291127501835804656529603983330304127768, 64639581064354157349746518765309305166295198913786821156885357341832971588844, 90354658228040593281300119754247779870329701927324901681798697523188730973033, 81401987979903580862392404586229550887556894433599857234113189812553019212068, 65298685556525832301482171825516369217697144412414009394249099549396780614524, 92349134325759014555606171432361003009117804710882007512683431101244819357154, 39394732129711855468318778879498680882419172115836685759980312734935432566454, 89214625742350879812979703430208753053162953323218138936231425180728813794449, 87951032840368764288085902531369588071408620709369928883374860974551615905037, 60041643006614697975386569737424841551182444106423440342092211624111120068440, 52134076763481562368967639851739622158152428322184528366399356626269315562251, 94460273205082809035309971217762374872749243209992347460192832060386367068612, 81830195945772515483993492042731806886511046889048054326081378383609107573139, 59927341466053806949392223156717407467992244223474305030831956923880506151818, 8751919290908691103794561570673927187109339646175952750394326252264933529062, 54591713702851027898905443928525737279007535818923698240211592382012374983446, 2140612416897646831206582069941332263923242007855261278594389244676754980256, 52417324316592882505143461851975632709758110493345908564966799857008914624366, 67465336731188637403089317771383723385475068909628487431163316746247923651300, 27199905960890285751217134356216526365658255922621785367716717678817928449249, 54473441396851065734077065293435462643909804742918929675879047353889181542133, 80510976090103305519296069614208687998853259233221264088240018787064439260513, 8058130903768026149187035175827909499988897221461529508000687843925051502655, 67156889287780792927386938935000448930480556972869381436437517903446774800552, 72201690705594722108901018434840511628961928552271222882717149213381438349100, 84683979048378610860209511563266111942843164474629561376116322648815861493665, 84303105224028516998747055916665218580859682882704053081074579698916784229642, 47309573725991488669494386361197419696625258114057186352396638593272407412257)
n = len(c)
M = Matrix(ZZ,n+1,n)

for i in range(n):
    M[i,i]=p
    M[40,i]=c[i]
L = M.LLL()

    
x = L[1]
flag = []
for i in x:
    c = abs(i)
    for j in range(1,255):
        t1 = c % j
        t2 = c // j
        if t1 == 0 and isPrime(t2):
            flag.append(j)

for i in flag:
    print(chr(i),end="")
"""
NSSCTF{F1nd_@_s3cR3t_NUMBER_1s_eAsy_4_U}
"""

Matrix1

Matrix 1_v1

• 题目附件如下：

from Crypto.Util.number import *
from os import urandom
from secret import flag

def pad(msg, length):
    return msg + urandom(length - len(msg))

n = 10
p = getPrime(256)
M1 = Matrix(Zmod(p), n, n, pad(flag[:len(flag)//2],n^2))
M2 = Matrix(Zmod(p), n, n, pad(flag[len(flag)//2:],n^2))

A = random_matrix(Zmod(p), n, n)
B = M1*A*M2^(-1)

print("p =", p)
print("A =", A.list())
print("B =", B.list())

Matrix 1_v2

Matrix 2