本篇博客主要介绍如下分解方法：

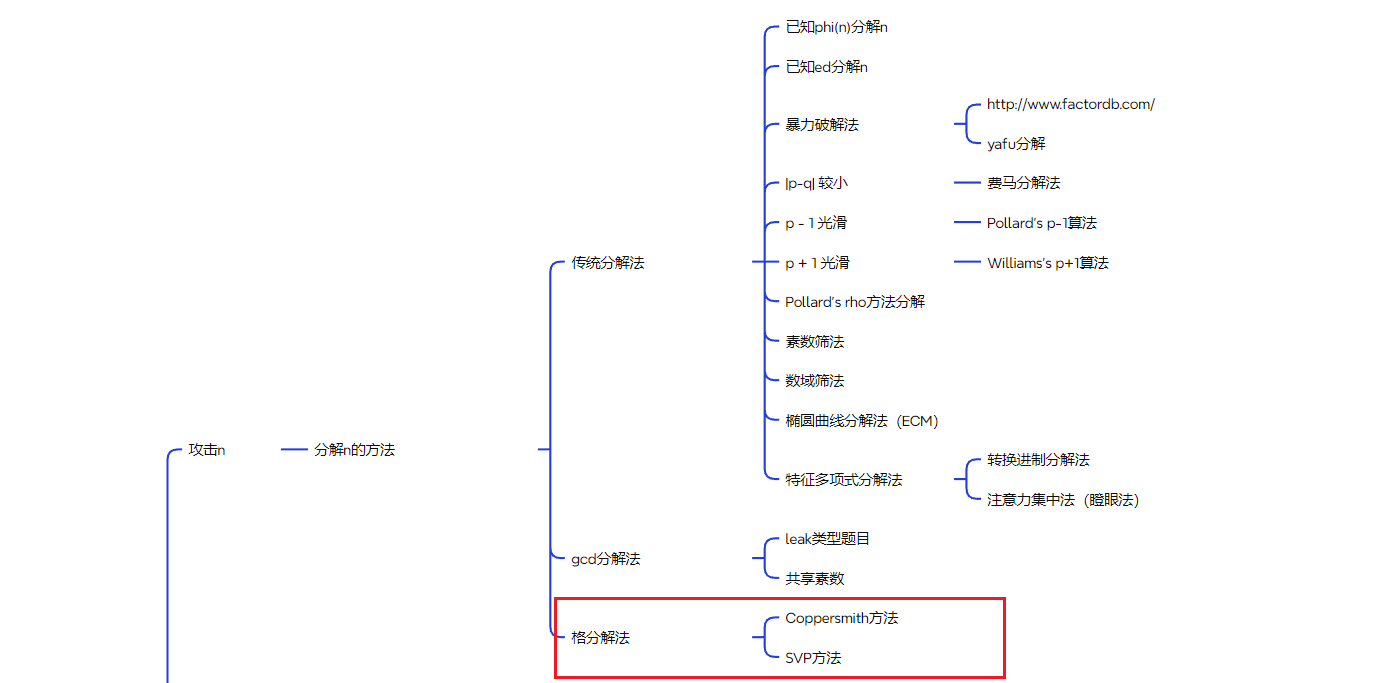
对于本次要学习的RSA分解相关的，都利用了关于私钥的一部分信息（这些信息通常假设未知的），来对模数进行分解。例如，攻击者可能已知私钥指数或模数中某个素因子的一部分比特。通过这些攻击可以看出，隐藏私钥比特的重要性。
一般来说，我们关注这样一个情形：私钥指数或模数中的某个素数的最高有效位(MSB)或者最低有效位(LSB)有一部分是已知的。设$0≤\varepsilon≤1$，表示已知比特所占的比例。对于最高有效位泄露的问题有如下定义，而对于最低有效位的情形，主要采用Boneh、Durfee、Frankel在论文中提出的一种更宽松的定义。
- 当已知一个数$x$的$\varepsilon$比例的最高有效位时，我们假设已知的一个近似值为$\hat{x}$使得：$x=\hat{x}+x_0$，其中未知量$x_0$满足：$|x_0|=|x-\hat{x}|<x^{1-\varepsilon}$
- 当已知$x$的$\varepsilon$比例的最低有效位，我们假设已知$\tilde{x}$以及一个满足$r≥|x^{\varepsilon}|$的参数$r$，使得$x=x_0r+\tilde{x}$，其中$|\tilde{x}|<r$，并且未知量$x_0$满足：$|x_0|=|\frac{x-\tilde{x}}{r}|<|\frac{x}{r}|<x^{1-\varepsilon}$。当$r=2^{l}$时，$\tilde{x}$就对应于通常意义下的$l$个最低有效比特。也就是说，在二进制表示中$x$与$\tilde{x}$的最低$l$位是相同的。
对于此类题目，基本上是$p$高位泄露、$p$低位泄露等等，我们都统称为带提示分解这一种分解题型。接下来大致介绍一下这类题型的解决方法以及要用到的相关定理。
- Coppersmith在论文中证明：当RSA模数是两个平衡素数时，如果已知其中一个素数的一半MSB，就可以将模数分解。
- Boneh、Durfee、Frankel发表论文证明：当RSA模数是两个平衡素数时，如果已知其中一个素数的一半LSB同样足以完成分解。
- 接下来给出定理6.1统一描述一下这个定理：
  - 设$N=pq$是一个由平衡素数（$p\approx q$）构成的RSA模数。如果已知其中一个素数的至少一半最高有效位或最低有效位，那么就可以在关于$log_N$的多项式时间内对$N$进行分解。
- 关于该定理的证明，我们可以使用Coppersmith的一元模多项式小根方法，给出该定理的证明。
  - 设$f(x)$是一个首一的一元一次多项式，$N$是一个未知因子分解的整数，并且存在一个未知因子$b>N^{\beta}$。这样只要满足$|x_0|<cN^{\beta^{2}}$，其中$c$是任意小的常数，那么所以满足$f(x_0)\equiv 0~mod(~b)$的根$x_0$都可以在多项式时间内被恢复出来。
- 证明MSB的情况：
  - 因为生成RSA模数的素数是两个平衡素数，所以就有$\frac{1}{2}N^{\frac{1}{2}}<p,q<2N^{\frac{1}{2}}$（这里放宽了$p$与$q$的大小顺序假设，不考虑$p、q$的大小关系）
  - 当已知模数中某个素数的LSB或MSB时，攻击的核心思想是：构造一个一元一次首一多项式，使其具有一个已知界限内的小根，该小根恰好对应于该素数中未知的那部分比特。一旦成功计算出这个小根，模数的因子分解也就被揭示出来。
  - 所以我们假设已知素数$p$的至少一半MSB，也就是说我们已知一个近似值$\hat{p}$，使得$p=\hat{p}+p0$，其中未知量$p_0$满足$|p_0|<|p-\hat{p}|<p^{\frac{1}{2}}<\sqrt{2}N^{\frac{1}{4}}$，注意到$p_0$是下面这个首一一元多项式在模意义下的小根$f{msb}(x)=x+\hat{p}$
  - 这是因为$f{msb}(p_0)=p_0+\hat{p}=p\equiv0 ~mod(~p)$，事实上由于$f{msb}(x)$是首一且一次的，多项式在模$p$意义下的所有根都可以写成$p_0+\alpha p$，其中$\alpha$是某个整数。因此，在所有的这些根中，只有$p_0$满足界限$|x|<\sqrt{2}N^{\frac{1}{4}}$。令$\beta=\frac{1}{2}-log_N(2),c=2\sqrt{2}$，注意到素数$p$满足$p>\frac{1}{2}N^{\frac{1}{2}}=N^{\frac{1}{2}-log_N(2)}=N^{\beta}$
  - 并且我们希望恢复的根满足：
  - 由Coppersmith方法中的相关定理，并结合上面所定义的常数$c$和$\beta$，可以推出我们能够计算该根$p_0$。因此由于$p=p_0+\hat{p}$我们就可以在关于$logN$的多项式时间内轻松完成对模数N的因子分解。
- 证明LSB的情况：
  - 接下来，假设我们已知素数$q$的至少一半LSB，也就是说，我们假设已知$\tilde{q}$和一个参数$r$，使得$q=q_0r+\tilde{q}$，其中$q=q_0r+\tilde{q}$以及$q^{\frac{1}{2}}<r<q$，并且未知量$q_0$满足$|q_0|=|\frac{q-\tilde{q}}{r}|≤|\frac{q}{r}|<q^{\frac{1}{2}}<2N^{\frac{1}{4}}$。
  - 当$r$是2的幂是，$\tilde{q}$就对应于$q$的真实最低有效位。令$R=r^{-1}~mod(~N)$，于是存在某个整数$k$值得：$rR=1+kN$。
  - 那么就可以注意到首一一元多项式：$f_{lsb}(x)=x+\tilde{q}R$有一个$q_0$是在模素数$q$下的根。
  - 很显然：$rf_{lsb}(q_0)=q_0r+\tilde{q}Rr=q_0r+\tilde{q}+\tilde{q}kN=q+\tilde{q}kpq\equiv 0~mod(~q)$
  - 由于在模数$q$意义下不存在零因子，并且条件$q^{\frac{1}{2}}<r<q$，包含了$r\not\equiv 0~mod(~q)$，因此可以得到$flsb(q_0)\equiv 0~mod(~q)$，与前一个多项式的情形完全类似，由于$f{lsb}(x)$是首一且线性的，所以在多项式模$q$意义1下的所有根中只有$q_0$能满足$|x|<\sqrt{2}N^{\frac{1}{4}}$
  - 由于该根的界限以及$N$的因子(即素数q)的大小界限与前一种情况完全相同，因此可以直接应用Coppersmith方法相关的定理，并使用之前完全相同的常数$c$和$\beta$，从而在关于$log(N)$的多项式时间内计算出根$q_0$。
  - 又因为$q=q_0r+\tilde{q}$，一旦求得$q_0$就立即得到了模数的因子分解。由于在整个推导过程中并未对素数$p、q$的大小顺序作任何假设，上述论证同样适用于：已知任意一个素数的$\frac{1}{2}$最高有效位和$\frac{1}{2}$最低有效位的情形，因此定理得证。
- 尽管上述结果要求：已知某个素数至少一半的最高有效位或最低有效位，但是这个界限实际上可以适当放宽，从而允许已知的比特比例略小一些。这一点可以直接从定理中的$|x|<cN^{\frac{1}{4}}$看出。常数$c$的存在，使得我们用可以略少的已知比特数，以增加运行时间为代价来完成攻击。
- 如果已知$\frac{1}{2}-\varepsilon$比例的比特，并且$\varepsilon\in O(log(logN))$那么整个攻击的运行时间仍然是关于$logN$的多项式时间。
- 另一种做法就是：对缺失的$\varepsilon$个比特进行穷举搜索，并对每一个关于那$\frac{1}{2}$已知比特的候选值尝试对模数进行分解，直到成功为止。
- 无论采取上述哪种方法，都可以得出结论：只要已知某个素数的大约一半的最高有效位或最低有效位，就可以高效地对RSA模数进行分解
接下来就直接看题了。

题型1 p高位泄露

p高位泄露例题1

题目附件如下：

from Crypto.Util.number import *
import uuid

p = getPrime(512)
q = getPrime(512)
n = p*q
e=65537
flag = "flag{"+str(uuid.uuid4())[:20]+"}"
m = bytes_to_long(flag.encode())
assert(m<n)
c=pow(m,e,n)

print(f"h = {((p>>128)<<128)}")
print(f"e = 65537")
print(f"c = {c}")
print(f"n = {n}")
"""
h = 9605964225476901441398365225327926616880072280289780777971846998748464126891804587377933727304510424852546683782576240573278202121547956666293242671661056
e = 65537
c = 2226099021169425534206121605501718994593261953280046899345810118356590881389142531649792348146129153474985003929407172972982275439970723778495455838452638879586163957468972518078320159354264971816842073874550773309020013613432004074760802192607651584906352686468143648939740004838208640531785439362344039075       
n = 96928253979490973984593903132811649229014718994486532280648145898877952846656019305217095845257550421730063527538581223570539203247068060192535543753763017716750817560470547219370972835770943358384150269303529653434434525449357699107332781898776312692702549420939758722366794431784782973884379040574148608179      
"""

根据上面说明的定理，我们只要已知超过一半的素数为就能分解，此题我们的素数位数是512位，而泄露p的512-128=384位，远远大于256位，那就可以直接用Coppersmith攻击求解。
构造首一一元模多项式：$f_{MSB}(x)=h+x~mod(~n)$，其中根的上界为$|x_0|<2^{128}$，$\beta=\sqrt{\frac{128}{1024}}=\sqrt{\frac{1}{8}}\approx0.3$应该可以求解出小根。
exp如下：

from Crypto.Util.number import *
h = 9605964225476901441398365225327926616880072280289780777971846998748464126891804587377933727304510424852546683782576240573278202121547956666293242671661056
e = 65537
c = 2226099021169425534206121605501718994593261953280046899345810118356590881389142531649792348146129153474985003929407172972982275439970723778495455838452638879586163957468972518078320159354264971816842073874550773309020013613432004074760802192607651584906352686468143648939740004838208640531785439362344039075       
n = 96928253979490973984593903132811649229014718994486532280648145898877952846656019305217095845257550421730063527538581223570539203247068060192535543753763017716750817560470547219370972835770943358384150269303529653434434525449357699107332781898776312692702549420939758722366794431784782973884379040574148608179      
PR.<x> = PolynomialRing(Zmod(n))
f = h + x 
result = f.small_roots(X=2^128,beta=0.3)
p = int(result[0] + h)
q = n // p
phi = (p-1)*(q-1)
d = inverse(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
# b'flag{c014bbe0-d90b-4249-b}'

p高位泄露例题2

题目来源：LitCTF 2023 Where is P? | NSSCTF
题目附件如下：

from Crypto.Util.number import *
m=bytes_to_long(b'XXXX')
e=65537
p=getPrime(1024)
q=getPrime(1024)
n=p*q
print(p)
c=pow(m,e,n)
P=p>>340
print(P)
a=pow(P,3,n)
print("n=",n)
print("c=",c)
print("a=",a)
#n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
#c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724
#a= 22184346235325197613876257964606959796734210361241668065837491428527234174610482874427139453643569493268653377061231169173874401139203757698022691973395609028489121048788465356158531144787135876251872262389742175830840373281181905217510352227396545981674450409488394636498629147806808635157820030290630290808150235068140864601098322473572121965126109735529553247807211711005936042322910065304489093415276688746634951081501428768318098925390576594162098506572668709475140964400043947851427774550253257759990959997691631511262768785787474750441024242552456956598974533625095249106992723798354594261566983135394923063605

题型2 p低位泄露

p低位泄露例题1

刷题

刷题1

题目来源：鹤城杯 2021BabyRSA | NSSCTF
题目附件如下：

from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag

p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724
hint2 = q % (2 ** 265)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)
"""
hint1 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
hint2 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
c = 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
"""

刷题2
题目来源：*CTF 2022ezRSA | NSSCTF
题目附件如下：

from Crypto.Util.number import getStrongPrime
from gmpy import next_prime
from random import getrandbits
from flag import flag

p=getStrongPrime(1024)
q=next_prime(p^((1<<900)-1)^getrandbits(300))
n=p*q
e=65537

m=int(flag.encode('hex'),16)
assert m<n
c=pow(m,e,n)

print(hex(n))
#0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3

print(hex(c))
#0xd7f6c90512bc9494370c3955ff3136bb245a6d1095e43d8636f66f11db525f2063b14b2a4363a96e6eb1bea1e9b2cc62b0cae7659f18f2b8e41fca557281a1e859e8e6b35bd114655b6bf5e454753653309a794fa52ff2e79433ca4bbeb1ab9a78ec49f49ebee2636abd9dd9b80306ae1b87a86c8012211bda88e6e14c58805feb6721a01481d1a7031eb3333375a81858ff3b58d8837c188ffcb982a631e1a7a603b947a6984bd78516c71cfc737aaba479688d56df2c0952deaf496a4eb3f603a46a90efbe9e82a6aef8cfb23e5fcb938c9049b227b7f15c878bd99b61b6c56db7dfff43cd457429d5dcdb5fe314f1cdf317d0c5202bad6a9770076e9b25b1

题型1 p高位泄露

p高位泄露 例题1

p高位泄露 例题2

题型2 p低位泄露

p低位泄露 例题1

刷题

刷题1

刷题2

p高位泄露例题1

p高位泄露例题2

p低位泄露例题1