RSA加密之小私钥攻击

• RSA加密对私钥的攻击比对公钥的攻击难多了，这篇博客主要讲解的就是RSA小私钥攻击，主要讲解如下内容，可能会分成两三篇博客进行记录，也可能只用一篇博客进行记录。

• 使用小私钥指数的RSA具有一定的风险。尽管在某些场景下，尽可能降低解密成本可能是比较有吸引力的，但如果私钥指数选择得过小，就会存在非常现实且有效的攻击，使得整个密码系统完全不安全。
• 在任何密码系统中，如果私钥（或秘密密钥）是从一个较小的集合中选取的，那么总是可以通过简单的穷举法搜索出来密钥从而破坏该系统。对RSA而言所有满足$d<2^{l}$的私钥指数$d$都可以直接通过猜测得到，其中$l$取决于当前技术的发展水平。例如，在目前的计算能力下，恢复所有满足$d≤2^{60}$的私钥指数是可行的，而对所有满足$d≤2^{80}$的私钥指数则是不可行的。
• 然而，接下来介绍的攻击方法，都能够恢复原大于简单穷举搜索所能覆盖范围的私钥指数。事实上，所有这些攻击都可以有效地攻破私钥指数大小达到$N^{\delta}$（其中$\delta ≥\frac{1}{4}$）的RSA实例。对于一个1024比特的模数，即便是这些攻击中最弱的一种，也已经可以破解私钥指数满足$d≤2^{256}$的RSA实例。
• 与前面几个攻击不太相同的是，那些攻击通常是在给定公钥以及一个或多个密文的情况下恢复一个或多个明文，然而针对小私钥指数RSA的所有攻击，都是利用密钥等式，仅凭借公钥就通过分解模数来彻底攻破RSA实例。
• 在以下攻击中，除非另有说明，我们将假设公钥指数和私钥指数都是在模$\lambda(N)$意义下定义的，并且二者都小于$\lambda(N)$。
• 由如下密钥等式：

$ed=1+k\lambda(N)$

• 我们可以推出如下一个不等式关系：

$0<k=\frac{ed-1}{\lambda(N)}<\frac{ed}{\lambda(N)}<min\{e,d\}$

• 特别地，由于本章关注的是小私钥指数RSA，因此有$k<d$。当指数是模$\phi(N)$定义时，同样的论证也依然成立。

维纳连分数攻击

维纳攻击 推导

• 第一个具有重大意义的RSA小私钥指数攻击就是维纳连分数攻击。仅仅只有公钥$(e,N)$，这个攻击可以使用$\frac{e}{N}$的连分数展开某个渐进分数所活动信息来分解模数。

• 这里还要介绍一个定理，该定理是勒让德连分数定理：

  • 设$\alpha\in R$，若有既约分数$|\alpha-\frac{p}{q}|<\frac{1}{2q^{2}}$
  • 那么$\frac{p}{q}$必然是$\alpha$的某一个连分数收敛子。

• 下面的定理最一般的形式重新描述了维纳连分数攻击，记该定理为定理5.1，定理内容如下：

  • 设$N=pq$是一个RSA的模数，设$e$是一个有效的公钥指数，并且$d$是定义在模$\lambda(N)$下与之对应的私钥指数。
  • 设$k$是一个满足密钥等式$ed=1+k\lambda(N)$的整数，$g=gcd(p-1,q-1)$，$g_0=\frac{g}{gcd(g,k)}$，以及$k_0=\frac{k}{gcd(k,g)}$
  • 如果私钥指数满足$d<\frac{pq}{2(p+q-1)g_0k_0}=\frac{N}{2sg_0k_0}$，那么$N$能在关于$log(N)$和$\frac{g}{k}$的多项式时间内被分解。
  • 证明如下：
    • 从新回顾一下RSA模数$N=pq$，$\lambda(N)=lcm(p-1,q-1)=\frac{\phi(N)}{gcd(p-1,q-1)}=\frac{N-s}{g}$，其中$g=gcd(p-1,q-1)$
    • 因此密钥等式可以重新写为$ed=1+k\lambda(N)=1+k\frac{\phi(N)}{g}=1+\frac{k_0gcd(k,g)}{g_0gcd(k,g)}(N-s)=1+\frac{k_0}{g_0}(N-s)$，其中$k_0=\frac{k}{gcd(k,g)},g_0=\frac{g}{gcd(k,g)}$，也最终其实就是这样的形式$ed=1+\frac{k_0}{g_0}(N-s)$
    • 接下来等式两边都同乘一个$dN$，就有$\frac{e}{N}=\frac{1}{dN}+\frac{k_0}{dg_0}-\frac{s}{dN}$。
    • 接下来再移项一下，就会出现$|\frac{e}{N}-\frac{k_0}{dg_0}|=|\frac{1}{dN}-\frac{k_0s}{dg_0N}|=|\frac{g_0-k_0s}{dg_0N}|<\frac{k_0s}{dg_0N}$，记为式子①
    • 假设私钥指数满足不等式$d<\frac{N}{2sg_0k_0}\Rightarrow \frac{1}{N}<\frac{1}{2sdg_0k_0}$
    • 使用假设私钥指数满足的不等式带入到式子①就会有$|\frac{e}{N}-\frac{k_0}{dg_0}|<\frac{k_0s}{dg_0N}<\frac{1}{2(dg_0)^{2}}$，记为式子②，这其实就满足了勒让德连分数定理的条件。
    • 有$\frac{k_0}{dg_0}$是$\frac{e}{N}$的一个收敛子，设$c_i=\frac{a_i}{b_i}$是连分数$\frac{e}{N}$的第$i$个收敛子，这下我们就知道$\frac{k_0}{dg_0}=\frac{a_j}{b_j}$。
    • 这样就有$ed=1+k\lambda(N)=1+k\frac{\phi(N)}{g}=1+\frac{k_0}{g_0}\phi(N)$。
    • 进而得到$\phi(N)=e(\frac{dg_0}{k_0})-\frac{g_0}{k_0}=\lfloor e(\frac{b_j}{a_j})\rfloor-\lfloor\frac{g_0}{k_0}\rfloor$
    • 因此如果我们知道正确的连分数$c_j$，并且可以猜到$\lfloor\frac{g_0}{k_0}\rfloor$，那不就可以得到$\phi(N)$了，当$\phi(N)$知道了，并且$N=pq$，那就可以直接列方程解出$p、q$了。所以维纳攻击实际上是一种完全攻击手段，可以间接分解出RSA的两个大素数。
  • 为了找到正确的连分数从而计算出$\phi(N)$，我们需要做如下操作：
    • 从$m=0$开始，我们通过迭代$\frac{e}{N}$的连分数收敛子来计算出$\phi(N)$的候选值，并计算$\phi'=\lfloor \frac{e}{c_i}\rfloor+m$
    • 对于每一个$\phi(N)$的候选值，我们尝试分解模数。如果没有任何候选值得到$\phi(N)$，我们就将$m$的值增加1，重新进行上面过程。
    • 通过这种方式，我们可以保证最终计算出候选的$\phi=\lfloor\frac{e}{c_j}\rfloor+\frac{g_0}{k_0}$，从而实现对模数$N$的因式分解。
    • 每一次测试（尝试使用$N$和$\phi(N)$的候选值来进行因式分解）是关于$log(N)$的多项式级别。由于$\frac{e}{N}$的连分数收敛子数量也是关于$log(N)$的多项式级别，并且对于每个收敛子我们最多测试$\frac{g_0}{k_0}=\frac{g}{k}$个候选值，最终结果得以实现。
  • 在证明中，获取正确的候选值的方法不是最优的。例如，当$|\frac{e}{N}-c_i|$太大，我们可以根据式子②忽略它。事实上，之后会讲到候选的连分数收敛子可以缩小到一个非常小的集合。
  • 此外，当RSA的质数是随机选择时，预期的$g$会非常小$g = gcd(p-1,q-1)$，因此，预期$\frac{g}{k}=0$，实际上只需要对候选连分数的收敛子进行一次迭代。在几乎所有的Wiener攻击的推导中，都假设在某个时刻$\frac{g}{k}=0$，或者$\frac{g}{k}<1$。
  • 上面定理5.1中的充分条件并不是通常与Wiener攻击相关的条件，更常见的条件是：

  $d<\frac{1}{c}N^{\frac{1}{4}}$

  • 对于某个小常数$c>1$，它是通过假设公钥指数大致与模数相同，并且生成$N$的素数满足平衡素数，并且$g_0$很小得出的。在一个典型的RSA实例中，当质数是随机生成并且私钥指数较小的时候，这些假设是有效的，这个界限大致上就是$d<N^{\frac{1}{4}}$是Wiener攻击的参考点（有时会被称为Wiener界限）

• 接下来举一个例子，在说明典型的小私钥指数RSA实例上进行攻击的过程：

  • 有公钥对$(e,N)=(58549809,2447482909)$，那么$\frac{e}{N}$的连分数为$[0,41,1,4,23,78,1,6,8,1,1,1,4,3,2]$
  • 先计算出一些收敛子$0,\frac{1}{41},\frac{1}{42},\frac{5}{209},\frac{116}{4849},\frac{9053}{378431},\frac{9169}{383280},\frac{64067}{2678111},...$
  • 测试上面的每一个目标收敛子，并且令$m=0$，前三个收敛子不能分解$N$
  • 到第四个收敛子，就有$\phi'=\lfloor\frac{e}{c_4}\rfloor=\lfloor58549809(\frac{209}{5})\rfloor=2447382016$
  • 通过已知$\phi(N)$分解$N$就可以得到$p=60317$和$q=40577$，这两个都是素数，因此$\phi(N)=\phi'$，并且我们分解了模数$N$。
  • 使用这个分解我们计算出，$\lambda(N)=611845504,g=4$，因此私钥对为$(d,p,q)=(209,60317,40577)$。
  • 此时就满足定理5.1的攻击条件，满足$d=209<\frac{N}{2sg_0k_0}\approx2425.82$

• 在一些非典型的RSA实例中，维纳攻击的效果可能比$N^{\frac{1}{4}}$更弱也可能更强，这个时候我们要牢牢抓住定理5.1的这个式子$d<\frac{pq}{2(p+q-1)g_0k_0}=\frac{N}{2sg_0k_0}$，有以下三种方式可以减小私钥指数的界限从而削弱攻击：

  • 使用不平衡的素数，使得$s=p+q-1$变得更大。
  • 使用具有大$g=gcd(p-1,q-1)$的质数，从而假定$g_0$也变得更大。
  • 使用$e>N$的公钥指数，使得$k\approx\frac{ed}{N}$（并假定$k_0$）变得更大。一个比$N$更大的公钥指数可以通过简单地将$\lambda(N)$的倍数加到现有的正常公钥指数上来实现。事实上，当$e>N^{\frac{3}{2}}$时，维纳攻击完全无效。
    • 较大的公钥指数削弱攻击，而较小的公钥指数则强化攻击。考虑使用平衡指数、小$g_0$、小私钥指数$d=N^{\delta}<N^{\frac{1}{2}}$和公钥指数$e=N^{\alpha}$的RSA，其中$\frac{1}{2}<\alpha<1$。由于$ed=1+k\lambda(N)$，我们有$k\approx N^{\alpha+\delta-1}$。将这些带入Wiener攻击的通用条件，并忽略小常数。就可以得到$N^{\delta}<N^{1-\frac{1}{2}-(\alpha+\delta-1)-\epsilon}$，或者更简单地$\delta<\frac{3}{4}-\frac{\alpha}{2}-\epsilon$，其中$\epsilon>0$是一个小常数，表示任何被忽略的小因子。
    • 在典型情况下，当$e\approx N$时，我们有$\alpha\approx1$以及$\delta<\frac{1}{4}$，这是预期的结果，对于较大的公钥指数，界限上的$\delta$会减小，直到在$\alpha=\frac{3}{2}$时消失，此时攻击无法保证任何结果，而对于较小的公钥指数，界限会增加，直到在$\alpha=\frac{1}{2}$时达到$\delta <\frac{1}{2}$

维纳攻击 例题1

• 题目来源：RSA入门 | DexterJie’Blog
• 题目附件如下：

import libnum
import random
import gmpy2

# 生成随机素数
p = libnum.generate_prime(512)
q = libnum.generate_prime(512)
m = "flag{20d6e2da95dcc1fa5f5432a436c4be18}"
# 字符串转数字
m = libnum.s2n(m)
n = p * q
phi_n = (p - 1) * (q - 1)

# 计算d
while True:
    nbits = 1024
    d = random.getrandbits(nbits // 4)
    if (libnum.gcd(d, phi_n) == 1 and 36 * pow(d, 4) < n):
        break
# 计算e
e = libnum.invmod(d, phi_n)

c = pow(m, e, n)

print("n=", n)
print("e=", e)
print("c=", c)
"""
n = 113881698992379349039968368927979997900777221951663104697020683691495129639829918739755194174063944178083527489820939138302751895652076620380510013941997706327553964127612610209509889011613768847759318892303231846117914554931459295347697888260576901354448014917692680573408654658384481284699735788978230690197
e = 39068960413447607023613035707248214114819409621234801785480423979473767995171860917209502861408393208940683687475760366491413173744775811644295874981290403938714121977201901942939425294427737703229098649131737380098596135730392902019429964095866394165971291108245774407908011073271822915371753470010435225545
c = 32897925577913728659288168937025744709859960639901500169867896018406263110205704273203287172003057450591000201857719871686024077615520906540631374442504017489026298422189715372129838501090730593164075113452055617571409044743698645392909829425374093273187125709095368164744188182156849031225036001381531504057
"""

维纳攻击 例题2

• 题目来源：XYCTF2024
• 题目附件如下：

import gmpy2
import hashlib
from Crypto.Util.number import *

p = getPrime(512)
q = getPrime(512)
d = getPrime(512)
e = gmpy2.invert(d, (p**3 - 1) * (q**3 - 1))
flag = "XYCTF{" + hashlib.md5(str(p + q).encode()).hexdigest() + "}"
print(e)
print(p * q)
# 172005065945326769176157335849432320425605083524943730546805772515111751580759726759492349719668775270727323745284785341119685198468883978645793770975366048506237371435027612758232099414404389043740306443065413069994232238075194102578269859784981454218948784071599231415554297361219709787507633404217550013282713899284609273532223781487419770338416653260109238572639243087280632577902857385265070736208291583497988891353312351322545840742380550393294960815728021248513046077985900158814037534487146730483099151396746751774427787635287611736111679074330407715700153025952858666841328055071403960165321273972935204988906850585454805923440635864200149694398767776539993952528995717480620593326867245714074205285828967234591508039849777840636255379730281105670496110061909219669860172557450779495125345533232776767292561378244884362014224844319802810586344516400297830227894063759083198761120293919537342405893653545157892446163
# 99075185389443078008327214328328747792385153883836599753096971412377366865826254033534293886034828804219037466246175526347014045811852531994537520303063113985486063022444972761276531422538694915030159420989401280012025249129111871649831185047820236417385693285461420040134313833571949090757635806658958193793

维纳攻击 板子

• 收集一下板子，通过解读板子所写的代码，对维纳攻击会有更深的体会。

维纳攻击 Python实现

import gmpy2
import libnum


def continuedFra(x, y):
    """计算连分数
    :param x: 分子
    :param y: 分母
    :return: 连分数列表
    """
    cf = []
    while y:
        cf.append(x // y)
        x, y = y, x % y
    return cf


def gradualFra(cf):
    """计算传入列表最后的渐进分数
    :param cf: 连分数列表
    :return: 该列表最后的渐近分数
    """
    numerator = 0
    denominator = 1
    for x in cf[::-1]:
        # 这里的渐进分数分子分母要分开
        numerator, denominator = denominator, x * denominator + numerator
    return numerator, denominator


def solve_pq(a, b, c):
    """使用韦达定理解出pq，x^2−(p+q)∗x+pq=0
    :param a:x^2的系数
    :param b:x的系数
    :param c:pq
    :return:p，q
    """
    par = gmpy2.isqrt(b * b - 4 * a * c)
    return (-b + par) // (2 * a), (-b - par) // (2 * a)


def getGradualFra(cf):
    """计算列表所有的渐近分数
    :param cf: 连分数列表
    :return: 该列表所有的渐近分数
    """
    gf = []
    for i in range(1, len(cf) + 1):
        gf.append(gradualFra(cf[:i]))
    return gf


def wienerAttack(e, n):
    """
    :param e:
    :param n:
    :return: 私钥d
    """
    cf = continuedFra(e, n)
    gf = getGradualFra(cf)
    for d, k in gf:
        if k == 0: continue
        if (e * d - 1) % k != 0:
            continue
        phi = (e * d - 1) // k
        p, q = solve_pq(1, n - phi + 1, n)
        if p * q == n:
            return d


n = 
e = 
c = 

d = wienerAttack(e, n)
print(d)
m = pow(c, d, n)
print(libnum.n2s(m).decode())

维纳攻击 sagemath实现

1

拓展维纳攻击

• 拓展维纳攻击，需要比较扎实的连分数基础和格攻击的基础。

Boneh and Durfee攻击

• 前面介绍了维纳攻击和拓展维纳攻击，维纳攻击可以看作是尝试在模$N$下简化的密钥方程。而Boneh和Durfee证明了一种更强大的攻击方法，即通过尝试在模公钥指数$e$下解决密钥方程。
• 具体而言，就是解如下同余方程：

$-k(N-s)\equiv 1~mod(~e)$

• 通过解这个方程中的未知数$k$和$s$，可以对私钥指数$d<N^{0.292}$的RSA进行启发式攻击。这是目前已知最强大的正对小私钥指数的RSA攻击之一，适用于平衡素数的情况，并且不需要是部分密钥泄露攻击或不需要素数的特殊性质。
• 在这部分攻击中展示的所有基于格的攻击，我们假设素数是平衡的，且公钥指数和私钥指数都是模$\phi(N)$下定义的。接下来要了解Boneh和Durfee对任意大小公钥指数的攻击完整的推导，并且简要介绍Blömer和May的变种。

Boneh and Durfee 攻击

Boneh and Durfee 攻击 推导

• 先重新陈述Boneh和Durfee针对小私钥指数RSA基于格的攻击，适用于任意公共指数。由于该结果依赖尚未证明的假设，我们只能将其表述为一种攻击方法，描述如下：

  • 对于任意的$\varepsilon >0$，都存在一个$n_0$，使得当$n>n_0$时如下结论成立
  • 设$N=pq$是一个n位的RSA模数，并且$p、q$是平衡素数；设$(e,N)$是有效的公钥对，设$d$是其对应的定义在模$\phi(N)$下的私钥指数
  • 设$e=N^{\alpha},d=N^{\delta}$，在给定公钥的情况下，如果私钥满足$\delta <\frac{7}{6}-\frac{1}{3}\sqrt{1+6\alpha}-\varepsilon$，那么只要满足两个假设，就可以在关于$log(N)$的多项式时间内对模数$N$进行分解。
  • 假设1：在$Z$或$Z_N$上具有已知小解的多项式，只存在唯一的一个小解。
  • 假设2：由LLL规约后的基向量所得到的这些多项式代数意义上彼此独立。

• 对于Boneh和Durfee攻击的说明：

  • 考虑密钥等式$ed=1+k(N-s)$，将这个密钥等式模$e$就可以得到：$kN-ks+1\equiv 0 ~mod(~e)$，其中$k$和$s$是未知量。
  • 这就启发我们寻找这个二元多项式的小根：$f_e(x,y)\in Z[x,y]: f_e(x,y)=Nx+xy+1$，其中$(x_0,y_0)=(k,-s)$是$f_e(x,y)$模$e$下的根。
  • 设$e=N^{\alpha}$和$d=N^{\delta}$，注意期望得到的根满足：
    • $|x_0|=k=\frac{ed-1}{\phi(N)}<\frac{ed}{\frac{1}{2}N}=2N^{\alpha+\delta-1}$
    • $|y_0|=|-s|=p+q-1<3N^{\frac{1}{2}}$
    • 其中我们使用的$\phi(N)>\frac{1}{2}N$并且$s<3N^{\frac{1}{2}}$因为加密使用的素数是平衡素数。
  • 因此就可以将这两个变量的界限分别定为：$X=2N^{\alpha+\delta-1}$和$Y=3N^{\frac{1}{2}}$，使用多项式$f_e(x,y)$和界限$X$和$Y$就可以构造一个格，使得该格中的每个元素都对应于一个多项式，并且该多项式在模$e$的某个幂意义下都以$(x_0,y_0)$为根。
  • 对某个固定的整数$m>0$，定义如下多项式：
    • $g_{i,k}(x,y):=x^{i}f_e(x,y)^{k}e^{m-k}$
    • $h_{j,k}(x,y):=y^{j}f_e(x,y)^{k}e^{m-k}$
    • 其中$g_{i,k}(x,y)$被称为x-移位，$h_{j,k}(x,y)$被称为y-移位。因为他们分别通过乘$x$或$y$的幂，对基础多项式$f_e(x,y)$进行位移。
  • 在这种构造下可以注意到：对于任意$i,j≥0$以及$0≤k≤m$，如果$(x_0,y_0)$是模$f_e(x,y)$在模$e$意义下的一个根，那么它同样也是$g_{i,k}(x,y)$和$h_{j,k}(x,y)$在模$e^{m}$意义下的一个根。也就是如下式子，下面这个式子是后续造格利用Coppersmith方法的关键基础：

  $f_e(x_0,y_0)\equiv 0~mod(~e)\Rightarrow \begin{cases} g_{i,k}(x_0,y_0)\equiv 0~mod(~e^{m})\\ h_{j,k}(x_0,y_0)\equiv 0~mod(~e^{m}) \end{cases}······①$

  • 接下来，利用多项式$g_{i,k}(xX,yY)$和$h_{j,k}(xX,yY)$的系数向量（其中$X$和$Y$是前面定义的$x_0$和$y_0$的界），我们可以造出一个格$L$的基矩阵$\mathbf{B}$。该格中的每个向量，都是多项式$g_{i,k}(xX,yY)$和$h_{j,k}(xX,yY)$的系数向量，而这个多项式$f(xX,yY)$正是由$g_{i,k}(xX,yY)$和$h_{j,k}(xX,yY)$整数线性组合得到的。
  • 于是由式子①就可以推出这些多项式$f(x,y)$中的每一个都满足如下性质：$f_e(x_0,y_0)\equiv 0~mod(~e)\rightarrow f(x_0,y_0)\equiv 0~mod(~e^{m})$
  • 因此每一个在格中的向量$v$都是相应的一个在模$e^m$下有根$(x_0,y_0)$的多项式$f(x,y)$，因此Boneh和Durfee所使用的基矩阵具体构造我们将其记为$\mathbf{B_{BD}}$是由如下多项式的系数向量所组成的，其中下面的整数$t>0$，并且具有如下特征：

  $\begin{array}{l} \{g_{i,k}(xX,yY)|0≤k≤m,0≤i≤m-k\}\\ \{h_{j,k}(xX,yY)|0≤k≤m,1≤j≤t\} \end{array}$

  • 对于造出来的基矩阵从行的角度看：
    • 有$\omega=\frac{(m+1)(m+2)}{2}+t(m+1)$总数个基向量并且它们都是线性无关的。
    • 因此这个格的维数为：$dim(L_{BD})=\omega$，并且行和列被重新排列使得这个基矩阵是下三角矩阵。
    • 对于行来说，自顶向下，首先是放置x-位移多项式$g_{i,k}(xX,yY)$，按照$l=i+k$的值递增排列，其中$l=0,...,m$；对于固定的$l$，这写多项式按照$k=0,...,l$的递增顺序排列
    • 接下来放置的是y-位移多项式$h_{j,k}(xX,yY)$，按照$j=1,...,t$的递增顺序排列；对于每个固定的$j$，这些多项式再按照$k=0,....,m$
    • 在这种向量的递增顺序排列下，每一个新的基向量都会恰好引入一个此前所以基向量都没有出现过的单项式。
  • 从列的角度看：
    • 对列从左到右进行排序，使得第$n$列对应的正是第$n$行所引入的那个单项式。具体来说就是前$\omega_x=\frac{(m+1)(m+2)}{2}$列对应的单项式$x^{i}y^{k}$，它们按照$i=0,...,m$递增排列，对于每个固定的$i$再按照$k=0,...,i$排列。这些对应的就是x-移位多项式中的单项式
    • 剩下的$\omega_y=t(m+1)$列对应的单项式，$x^{k}y^{j+k}$它们按照$j=1,...,t$递增排列，对于每个固定的$j$，再按照$k=0,...,m$递增排列。这些列对应的是只出现在y-移位多项式中的单项式。
  • 在下图中，当$m=2、t=1$时，给出了这种排序下的基矩阵$B_{BD}$，在这种基矩阵的排序方式下，其对角线元素为
    • 对于x-位移多项式对角线的元素是：$X^{i+k}Y^{k}e^{m-k}$
    • 对于y-位移多项式对角线的元素是：$X^{k}Y^{j+k}e^{m-k}$
    • 由于$vol(L_{BD})=|det(B_{BD})|$，而$B_{BD}$的行列式在这里仅仅等于其对角线元素的乘积，因此格$L_{BD}$的体积很容易计算出来。
    • 计算结果为：$vol(L_{BD})=(\Pi^{m}_{k=0}\Pi^{m-k}_{i=0}X^{i+k}Y^{k}e^{m-k})(\Pi^{m}_{k=0}\Pi^{t}_{j=1}X^{k}Y^{j+k}e^{m-k})=(eX)^{\frac{m(m+1)(m+2)}{3}+\frac{tm(m+1)}{2}}Y^{\frac{m(m+1)(m+2)}{6}+\frac{t(m+1)(m+t+1)}{2}}$
    • 其中第一个双重乘积对应于来自x-位移多项式的贡献(这样的多项式有$\omega_x$个)，第二个双重乘积对应于y-位移多项式的贡献（这样的多项式有$\omega_y$个）。

  

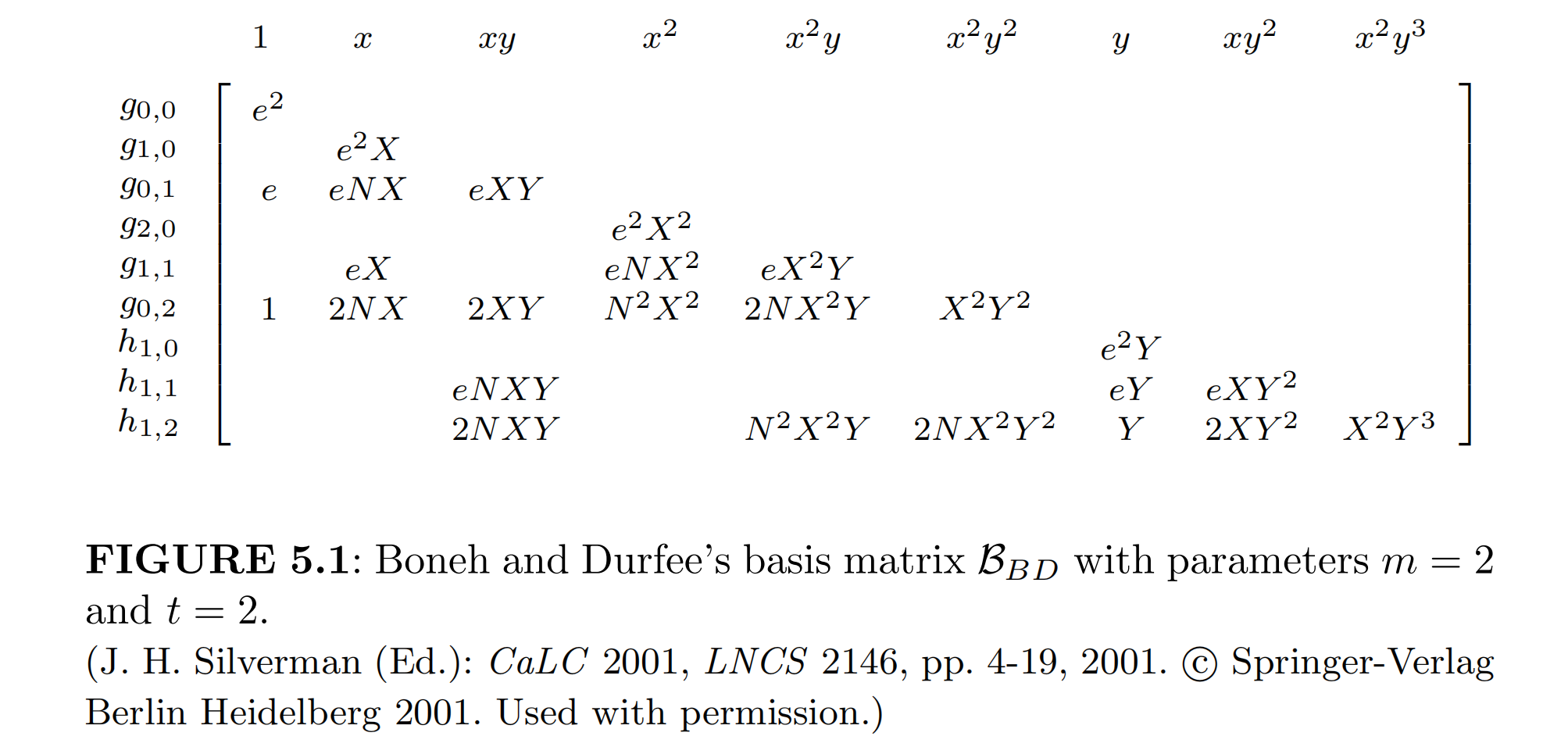
  • 对格$L_{BD}$使用LLL算法计算出规约后的基向量，由Coppersmith方法以及对应的多项式结论就可以得到，规约后的基向量最小的两个向量对应于线性无关的多项式$p_1(x,y),p_2(x,y)$，它们满足：$||p_1(xX,yY)||≤||p_2(xX,yY)||≤2^{\frac{\omega}{4}}vol^{\frac{1}{\omega-1}}$
  • 如果这两个多项式中较大的哪个也满足$||p_2(xX,yY)||<\omega^{-\frac{1}{2}}e^{m}$，那么根据Howgrave-Graham的结果，并将其应用到二元多项式的情形，我们知道$(x_0,y_0)$是多项式$p_1(x,y)$和$p_2(x,y)$在整数环上的一个公共根。满足这个公共根的一个充分条件就是：$2^{\frac{\omega}{4}}vol(L)^{\frac{1}{\omega-1}}<\omega^{-\frac{1}{2}}e^{m}$
  • 或者更简单地写成：$vol(L)<2^{\frac{-\omega(\omega-1)}{4}}\omega^{\frac{-(\omega-1)}{2}}e^{m(\omega-1)}=\gamma e^{m(\omega-1)}$，该式记为③式，其中：$\gamma=2^{\frac{-\omega(\omega-1)}{4}}\omega^{\frac{-(\omega-1)}{2}}$，是一个常数（当m和t固定的时候），这是该攻击能够成功的条件

• 只要格$L_{BD}$的体积满足上述不等式，多项式$p_1(x,y)$和$p_2(x,y)$就都以$(x_0,y_0)$作为其整数意义下的一个根。如果这两个多项式在代数上相互独立，那么我们就可以对$p_1(x,y)$和$p_2(x,y)$关于变量x计算它们的结式，从而得到一个多项式：$p_{1,2}(y)$该多项式在整数上以$y_0=-s$作为根。

• 接着，可以使用标准的一元整数多项式求根技术来求出$y_0$，当$s$已知之后，我们就可以计算：$\phi(N)=N-s$，并且很容易地对模数$N$进行因数分解。

• 需要注意的是，上述结论对于所有满足$|x_0'|<X$以及$|y_0'|<Y$的、使得$f_e(x,y)\equiv 0~mod(~e)$的根$(x_0',y_0')$都成立。我们假设只存在唯一的解（上面描述过的假设）

• 尽管这个使能条件在理论上是完全正确的，但是它并没有针对$\alpha$和$\delta$等输入参数，提供关于该攻击成功性的太多直观认识。为了推导出一个更有用的使用条件，尤其是攻击结论所给出的条件，我们需要做出一些假设并进行简化。

  • 首先我们忽略③式中$\gamma=2^{\frac{-\omega(\omega-1)}{4}}\omega^{\frac{-(\omega-1)}{2}}$，因为一但$m$和$t$被选定，这个因子就是一个固定常数，通常考虑足够大的$N$，也就是$e$会比较大，这个固定常数就可以被认为是很小，可以忽略不计
  • 接下来将$X=2N^{\alpha+\delta-1},Y=3N^{\frac{1}{2}},e=N^{\alpha}$，代入到使能条件中，并设：$t=\tau m$其中$\tau>0$为某个实数，与处理$\gamma$的方式相同，我们忽略$X$和$Y$中的小常数因子。
  • 得出忽略后有不等式：$N^{(\frac{\tau^2}{4}+(\alpha+\frac{\delta}{2}-\frac{1}{4})+\frac{2\alpha}{3}+\frac{\delta}{3}-\frac{1}{4})m^{3}+o(m^{3})}<N^{(\alpha\tau+\frac{\alpha}{2})m^{3}+o(m^3)}$，其中我们只保留了来自$m^3$项的贡献。对于足够大的$m$（这可能需要考虑更大的$N$，以保证$\gamma$仍然可以忽略），我们可以使所以$o(m^3)$级别的贡献变得任意小。忽略这些低阶项，我们只关注$m^3$项的系数，关于指数的条件就可以被简化：$\frac{1}{4}\tau^{2}+(\frac{\delta}{2}-\frac{1}{4})\tau+\frac{\alpha}{6}+\frac{\delta}{3}-\frac{1}{4}<0$
  • 注意对于任意的$\alpha$和$\delta$，当$\tau=\tau_{min}=\frac{1}{2}-\delta$时，该不等式的左端取得最小值。将这一取值代回不等式并重新整理后，可以得到

  $-\frac{1}{4}\delta^{2}+\frac{7}{12}\delta+\frac{\alpha}{6}-\frac{5}{16}<0$

  • 解出这个不等式就会得到新的使用条件：$\delta<\frac{7}{6}-\frac{1}{3}\sqrt{1+6\alpha}-\varepsilon$，其中加入了一个$\varepsilon>0$用来补偿前面被忽略的常数因子以及被舍弃的低阶项。通过取足够大的$N$和$m$，这个修正项可以被做的任意接近于零
  • 因此对于足够大的$N$，如果私钥指数$d=N^{\delta}$，满足使用条件$\delta<\frac{7}{6}-\frac{1}{3}\sqrt{1+6\alpha}-\varepsilon$那么就可以找到两个以$(x_0,y_0)=(k,-s)$为根的多项式。如果这两个多项式在代数上相互独立，那么就可以计算出$y_0=-s$，并利用它对模数进行分解，由于所以计算都可以在关于$log(N)$的多项式时间内完成，因此结论成立。
  • 在一个典型的小私钥指数RSA实例中，公钥指数的大小通常与模数的大小大致相同，使用近似的上述攻击中的条件就可以转换为$\delta<\frac{7}{6}-\frac{1}{3}\sqrt{1+6\alpha}-\varepsilon$，因此，对于足够大的模数，如果所使用的私钥指数满足上述界限，RSA将被认为是不安全的。

Boneh and Durfee 攻击 例题1

Boneh and Durfee 攻击 例题2

Boneh and Durfee 攻击 板子

• sagemath板子如下：

import time

"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True

"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct 
upperbound on the determinant. Note that this 
doesn't necesseraly mean that no solutions 
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False

"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension

############################################
# Functions
##########################################

# display stats on helpful vectors
def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii,ii] >= modulus:
            nothelpful += 1

    print (nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")

# display matrix picture with 0 and X
def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii,jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        print (a)

# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
    # end of our recursive function
    if current == -1 or BB.dimensions()[0] <= dimension_min:
        return BB

    # we start by checking from the end
    for ii in range(current, -1, -1):
        # if it is unhelpful:
        if BB[ii, ii] >= bound:
            affected_vectors = 0
            affected_vector_index = 0
            # let's check if it affects other vectors
            for jj in range(ii + 1, BB.dimensions()[0]):
                # if another vector is affected:
                # we increase the count
                if BB[jj, ii] != 0:
                    affected_vectors += 1
                    affected_vector_index = jj

            # level:0
            # if no other vectors end up affected
            # we remove it
            if affected_vectors == 0:
                print ("* removing unhelpful vector", ii)
                BB = BB.delete_columns([ii])
                BB = BB.delete_rows([ii])
                monomials.pop(ii)
                BB = remove_unhelpful(BB, monomials, bound, ii-1)
                return BB

            # level:1
            # if just one was affected we check
            # if it is affecting someone else
            elif affected_vectors == 1:
                affected_deeper = True
                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
                    # if it is affecting even one vector
                    # we give up on this one
                    if BB[kk, affected_vector_index] != 0:
                        affected_deeper = False
                # remove both it if no other vector was affected and
                # this helpful vector is not helpful enough
                # compared to our unhelpful one
                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
                    print ("* removing unhelpful vectors", ii, "and", affected_vector_index)
                    BB = BB.delete_columns([affected_vector_index, ii])
                    BB = BB.delete_rows([affected_vector_index, ii])
                    monomials.pop(affected_vector_index)
                    monomials.pop(ii)
                    BB = remove_unhelpful(BB, monomials, bound, ii-1)
                    return BB
    # nothing happened
    return BB

""" 
Returns:
* 0,0   if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May
    
    finds a solution if:
    * d < N^delta
    * |x| < e^delta
    * |y| < e^0.5
    whenever delta < 1 - sqrt(2)/2 ~ 0.292
    """

    # substitution (Herrman and May)
    PR.<u, x, y> = PolynomialRing(ZZ)
    Q = PR.quotient(x*y + 1 - u) # u = xy + 1
    polZ = Q(pol).lift()

    UU = XX*YY + 1

    # x-shifts
    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
            gg.append(xshift)
    gg.sort()

    # x-shifts list of monomials
    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials():
            if monomial not in monomials:
                monomials.append(monomial)
    monomials.sort()
    
    # y-shifts (selected by Herrman and May)
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift) # substitution
    
    # y-shifts list of monomials
    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            monomials.append(u^kk * y^jj)

    # construct lattice B
    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)

    # Prototype to reduce the lattice
    if helpful_only:
        # automatically remove
        BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
        # reset dimension
        nn = BB.dimensions()[0]
        if nn == 0:
            print ("failure")
            return 0,0

    # check if vectors are helpful
    if debug:
        helpful_vectors(BB, modulus^mm)
    
    # check if determinant is correctly bounded
    det = BB.det()
    bound = modulus^(mm*nn)
    if det >= bound:
        print ("We do not have det < bound. Solutions might not be found.")
        print ("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print ("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print ("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

    # display the lattice basis
    if debug:
        matrix_overview(BB, modulus^mm)

    # LLL
    if debug:
        print ("optimizing basis of the lattice via LLL, this can take a long time")

    BB = BB.LLL()

    if debug:
        print ("LLL is done!")

    # transform vector i & j -> polynomials 1 & 2
    if debug:
        print ("looking for independent vectors in the lattice")
    found_polynomials = False
    
    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):
            # for i and j, create the two polynomials
            PR.<w,z> = PolynomialRing(ZZ)
            pol1 = pol2 = 0
            for jj in range(nn):
                pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
                pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)

            # resultant
            PR.<q> = PolynomialRing(ZZ)
            rr = pol1.resultant(pol2)

            # are these good polynomials?
            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print ("found them, using vectors", pol1_idx, "and", pol2_idx)
                found_polynomials = True
                break
        if found_polynomials:
            break

    if not found_polynomials:
        print ("no independant vectors could be found. This should very rarely happen...")
        return 0, 0
    
    rr = rr(q, q)

    # solutions
    soly = rr.roots()

    if len(soly) == 0:
        print ("Your prediction (delta) is too small")
        return 0, 0

    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]

    #
    return solx, soly

def example():
    ############################################
    # How To Use This Script
    ##########################################

    #
    # The problem to solve (edit the following values)
    #

    # the modulus
    N = 0xbadd260d14ea665b62e7d2e634f20a6382ac369cd44017305b69cf3a2694667ee651acded7085e0757d169b090f29f3f86fec255746674ffa8a6a3e1c9e1861003eb39f82cf74d84cc18e345f60865f998b33fc182a1a4ffa71f5ae48a1b5cb4c5f154b0997dc9b001e441815ce59c6c825f064fdca678858758dc2cebbc4d27
    # the public exponent
    e = 0x11722b54dd6f3ad9ce81da6f6ecb0acaf2cbc3885841d08b32abc0672d1a7293f9856db8f9407dc05f6f373a2d9246752a7cc7b1b6923f1827adfaeefc811e6e5989cce9f00897cfc1fc57987cce4862b5343bc8e91ddf2bd9e23aea9316a69f28f407cfe324d546a7dde13eb0bd052f694aefe8ec0f5298800277dbab4a33bb

    # the hypothesis on the private exponent (the theoretical maximum is 0.292)
    delta = 0.280 # this means that d < N^delta

    #
    # Lattice (tweak those values)
    #

    # you should tweak this (after a first run), (e.g. increment it until a solution is found)
    m = 4 # size of the lattice (bigger the better/slower)

    # you need to be a lattice master to tweak these
    t = int((1-2*delta) * m)  # optimization from Herrmann and May
    X = 2*floor(N^delta)  # this _might_ be too much
    Y = floor(N^(1/2))    # correct if p, q are ~ same size

    #
    # Don't touch anything below
    #

    # Problem put in equation
    P.<x,y> = PolynomialRing(ZZ)
    A = int((N+1)/2)
    pol = 1 + x * (A + y)

    #
    # Find the solutions!
    #

    # Checking bounds
    if debug:
        print ("=== checking values ===")
        print ("* delta:", delta)
        print ("* delta < 0.292", delta < 0.292)
        print ("* size of e:", int(log(e)/log(2)))
        print ("* size of N:", int(log(N)/log(2)))
        print ("* m:", m, ", t:", t)

    # boneh_durfee
    if debug:
        print ("=== running algorithm ===")
        start_time = time.time()

    solx, soly = boneh_durfee(pol, e, m, t, X, Y)

    # found a solution?
    if solx > 0:
        print ("=== solution found ===")
        if False:
            print ("x:", solx)
            print ("y:", soly)

        d = int(pol(solx, soly) / e)
        print ("private key found:", d)
    else:
        print ("=== no solution was found ===")

    if debug:
        print("=== %s seconds ===" % (time.time() - start_time))

if __name__ == "__main__":
    example()

Boneh and Durfee 子格攻击

Blömer and May攻击

共模攻击

共模攻击 推导

共模攻击 例题1

共私钥攻击

• 共私钥攻击这里我们只介绍正常的RSA加密的共私钥攻击，对于多模数和多幂的RSA情况之后再学习。

共私钥攻击 推导

共私钥攻击 例题1