共模攻击

共模攻击 推导

共模攻击 例题1

共私钥攻击

  • 其实共私钥攻击在强网拟态2026出现过了，早就想写博客了，但是没时间，现在有时间写了，强网拟态2026的模数是多平衡素数的，而我们先来介绍两个平衡素数的情况。

  • 共私钥攻击这里我们只介绍正常的RSA加密的共私钥攻击，对于多模数和多幂的RSA情况之后再学习。在这个部分，我们将表明当把Wiener的小私钥攻击视为一种基于格的启发式攻击时，它可以很容易地被扩展，用来攻击多个RSA实例，只要这些实例共享同一个较小的私钥指数即可。所以这个攻击就被称为是共私钥攻击。

  • 当可用的实例数量增加时，该攻击的效果也会随之增强。对于这种攻击的情况，我们定义如下：

    • 假设同一个用户使用相同的较小的私钥指数dd，生成了rr个RSA实例，并且模数的大小也大致相同。
    • 设(ei,Ni),i=1,...,r(e_i,N_i),i=1,...,r是有效的RSA公钥对，并且Ni,i=1,...,rN_i,i=1,...,r的位数相差不大，dd是它们对应的私钥，并且dd比较小。
    • 这样我们就考虑如下rr个密钥等式：

    e1d=1+k1ϕ(N1)⋮erd=1+krϕ(Nr)e_1d=1+k_1\phi(N_1)\\ \vdots \\ e_rd=1+k_r\phi(N_r)

    • 其中，根据我们在前面了解RSA密码最开始介绍的有ϕ(Ni)=Ni−si\phi(N_i)=N_i-s_i，并且对于每个i=1,...,ri=1,...,r都有ki<dk_i<d
    • 接下来我们要保证所有模数的大小都是相同量级(模数的位数要相同)，并且将模数NiN_i进行按从大到小递增排列使得：N1<N2<...<Nr<2N1N_1<N_2<...<N_r<2N_1
    • 此外我们假设每个模数NiN_i都是由平衡素数生成的，即对于每个i=1,..,ri=1,..,r都有：∣si∣<3Ni12|s_i|<3N^{\frac{1}{2}}_i

  • 这就是共私钥能被攻击的前置条件，共私钥攻击的攻击方式可以在这篇论文中有详细的：IJCSI-9-2-1-311-314.pdf

共私钥攻击 推导

  • 我们先来讲解一下这个攻击的结论：

    • 任意整数r≥1r≥1，设N1,N2,...,NrN_1,N_2,...,N_r是平衡的RSA模数，并且满足N1<N2<...<Nr<2N1N_1<N_2<...<N_r<2N_1。
    • 设(e1,N1),...,(er,Nr)(e_1,N_1),...,(e_r,N_r)是有效的RSA公钥对，并且这些公钥对有相同的私钥指数d<Nrδrd<N^{\delta_r}_r。
    • 如果δr<12−12(r+1)−logNr(6)\delta_r<\frac{1}{2}-\frac{1}{2(r+1)}-log_{N_r}(6)，所有的模数都可以在关于log(Nr)log(N_r)以及rr的多项式时间内被分解。

  • 证明如下：

    • 令M=⌊Nr12⌋M=\lfloor N^{\frac{1}{2}}_r\rfloor（取将这些模数中最大的一个开根号），已知这rr个公钥对(e1,N1),...,(er,Nr)(e_1,N_1),...,(e_r,N_r)。
    • 继续考虑rr个密钥等式，eid=1+ki(Ni−si)e_id=1+k_i(N_i-s_i)，以及恒等式dM=dMdM=dM，我们将这些式子写成如下形式：

    dM=dMe1d−N1k1=1−k1s1e2d−N2k2=1−k2s2⋮⋱⋮⋮erd−Nrkr=1−krsr\begin{array}{l} dM&& & & & & = &dM\\ e_1d&-N_1k_1&&&&& =& 1&-k_1s_1\\ e_2d&&-N_2k_2&&&& = &1&-k_2s_2\\ \vdots&&&\ddots&&&\vdots &\vdots\\ e_rd&&&&-N_rk_r&& = &1&-k_rs_r\\ \end{array}

    • 这个系统中的的r+1r+1个等式可以写成向量矩阵方程xrBr=vrx_r\mathbf{B_r}=v_r：

    xr=(d,k1,...,kr)Br=[Me1e2…er−N1−N2⋱−Nr]vr=(dM,1−k1s1,...,1−krsr)\begin{array}{l} x_r=(d,k_1,...,k_r)\\ \mathbf{B_r}= \begin{bmatrix} M& e_1& e_2& \dots & e_r \\ &-N_1& & & \\ && -N_2&&\\ &&&\ddots&\\ &&&&-N_r \end{bmatrix} \\ v_r=(dM,1-k_1s_1,...,1-k_rs_r) \end{array}

    • 注意：此时目标向量vrv_r是矩阵BrB_r的每一行正线性组合而成的向量，因此这个向量是由格LrL_r所创造（或者说目标向量在我们所造的格LrL_r上），其中格基为是矩阵BrB_r每一行构成的一个基。
    • 由于有Ni≤Nr≤2N1,k＜d＜NrδrN_i≤N_r≤2N_1,k＜d＜N^{\delta_r}_r，并且还有si<3Nr12s_i<3N^{\frac{1}{2}}_r，对于任意i=1,...,ri=1,...,r都满足。
    • 这就是使得目标向量满足：∣∣vr∣∣<1+9rNr12+δr||v_r||<\sqrt{1+9r}N^{\frac{1}{2}+\delta_r}_r，就满足：

    ∣∣vr∣∣2=(dM)2+(1−k1s1)2+⋅⋅⋅+(1−krsr)2<(1+9r)(Nrδr+12)2||v_r||^2 = (dM)^ 2 + (1 − k_1s_1) ^2 + ··· + (1 − k_rs_r)^ 2 < (1 + 9r) (N_r ^{δ_r+\frac{1}{2}} )^2

    • 而这个格LrL_r的体积就为vol(Lr)=∣det(Br)∣vol(L_r)=|det(\mathbf{B_r})|，满足：

    vol(L)=∣MΠi=1r(−Ni)∣=⌊Nr12⌋Πi=1rNi>N112N1r>(Nr2)r+12vol(L)=|M\Pi^{r}_{i=1}(-N_i)|=\lfloor N_r^{\frac{1}{2}}\rfloor\Pi^{r}_{i=1}N_i>N_1^{\frac{1}{2}}N_1^{r}>(\frac{N_r}{2})^{r+\frac{1}{2}}

    • 从闵科夫斯基界限可以得到，目标向量是格LrL_r（该格的维数是r+1r+1）最短向量的必要条件是∣∣vr∣∣<r+1vol(Lr)1r+1||v_r||<\sqrt{r+1}vol(L_r)^{\frac{1}{r+1}}
    • 使用目标向量的范数作为界限，以及上面推导的格的体积，使上面必要条件成立的一个充分条件就是：

    9r+1Nrδ+12<r+1(Nr2)r+12r+1\sqrt{9r+1}N_r^{\delta+\frac{1}{2}}< \sqrt{r+1}(\frac{N_r}{2})^{\frac{r+\frac{1}{2}}{r+1}}

    • 或者更简单的不等式为，其中cr=r+19r+112r+12r+1>(13)(12)=16c_r=\sqrt{\frac{r+1}{9r+1}}\frac{1}{2^{\frac{r+\frac{1}{2}}{r+1}}}>(\frac{1}{3})(\frac{1}{2})=\frac{1}{6}

    Nr12+δr<crNrr+12r+1N_r^{\frac{1}{2}+\delta_r}<c_rN_r^{\frac{r+\frac{1}{2}}{r+1}}

    • 一个新的充分条件如下：Nr12+δr<16Nrr+12r+1=Nrr+12r+1−logN(6)N_r^{\frac{1}{2}+\delta_r}<\frac{1}{6}N_r^{\frac{r+\frac{1}{2}}{r+1}}=N_r^{\frac{r+\frac{1}{2}}{r+1}-log_N(6)}，通过解这个δr\delta_r就可以得到最后的不等式条件：

    δr<12−12(r+2)−logNr(6)\delta_r<\frac{1}{2}-\frac{1}{2(r+2)}-log_{N_r}(6)

    • 当私钥指数比NrδrN^{\delta_r}_r小的时候，我们就可以知道目标向量vrv_r满足了必要条件，已经满足了闵科夫斯基界限所施加的必要条件，从而有可能成为格LrL_r中的最短向量。此外，第二个标准也满足了。
    • 具体而言，当δr<12\delta_r<\frac{1}{2}，目标向量vrv_r比基矩阵B\mathbf{B}中的任何一个基向量的大小都要小。因此当私钥指数足够小，并且在格中的假设对格LrL_r成立，我们就能通过求解格LrL_r上的SVP问题从而求解出目标向量。一旦获得了目标向量，我们就能很轻松的分解所有的模数。
    • 从密钥等式可以入手：eid=1+ki(Ni−si)⇒ki=eid−(1−kisi)Nie_id=1+k_i(N_i-s_i)\Rightarrow k_i=\frac{e_id-(1-k_is_i)}{N_i}，而目标向量vr=(dM,1−k1s1,...,1−krsr)v_r=(dM,1-k_1s_1,...,1-k_rs_r)，这时目标向量就会暴露出私钥指数dd以及(1−kisi)(1-k_is_i)。暴露出这些后，我们就可以计算出kik_i。有了dd和kik_i从而计算出ϕ(Ni)=(eid−1)ki\phi(N_i)=\frac{(e_id-1)}{k_i}
    • 计算出ϕ(Ni)\phi(N_i)后，这就是前面的已知ϕ(Ni)\phi(N_i)分解NN的知识点了，两个素数的情况解方程就行了。

  • 这里也将书上的例子给出：

    • 下面有三对RSA公私钥对，它们有相同的私钥指数

    (e1,N1)=(587438623,2915050561)(e2,N2)=(2382816879,3863354647)(e3,N3)=(2401927159,3943138939)\begin{array}{l} (e_1,N_1)=(587438623,2915050561)\\ (e_2,N_2)=(2382816879,3863354647)\\ (e_3,N_3)=(2401927159,3943138939) \end{array}

    • 令M=⌊M312⌋=62794M=\lfloor M_3^{\frac{1}{2}}\rfloor=62794，我们构造出基矩阵：

    B=[62794587438623238281687924019271590−2915050610000−38633546470000−3943138939]\mathbf{B}= \begin{bmatrix} 62794 &587438623 & 2382816879 & 2401927159\\ 0& -291505061 &0&0\\ 0&0&-3863354647&0\\ 0&0&0&-3943138939 \end{bmatrix}

    • 使用LLL算法对基矩阵B\mathbf {B}进行格基规约，则规约出来的最短向量为b=(−41130070,14375987,50221643,50147516)b=(-41130070,14375987,50221643,50147516)
    • 如果攻击成功，我们预期b的第一个分量b1b_1满足∣b1∣=Md|b_1|=Md，我们有b1M=∣−41130070∣62794=655\frac{b_1}{M}=\frac{|-41130070|}{62794}=655，这个其实就是公共的私钥指数dd。
    • 在这个例子中，注意到攻击的使用条件：δ<12−12(r+1)−logN3(6)≈0.3189\delta<\frac{1}{2}-\frac{1}{2(r+1)}-log_{N_3}(6)\approx 0.3189满足条件，因为logN3(d)≈0.2935log_{N_3}(d)\approx 0.2935，那就满足了：d≈N30.2935<N0.3189<Nδd\approx N_3^{0.2935}<N^{0.3189}<N^{\delta}

共私钥攻击 例题1

  • 题目来源：nssCTF格密码工坊

  • 题目附件如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from Crypto.Util.number import *

flag = b'******'
flag = bytes_to_long(flag)
d = getPrime(400)




for i in range(4):
    p = getPrime(512)
    q = getPrime(512)
    n = p * q
    e = inverse(d, (p-1)*(q-1))
    c = pow(flag, e, n)
    print(f'e{i} =', e)
    print(f'n{i} =', n)
    print(f'c{i} =', c)

'''
e0 = 14663634286442041092028764808273515750847961898014201055608982250846018719684424125895815390624536073501623753618354026800118456911536861815261996929625814961086913500837475340797921236556312296934664701095834187857404704711288771338418177336783911864595983563560080719582434186801068157426993026446515265411
n0 = 104543450623548393448505960506840545298706691237630183178416927557780858213264769135818447427794932329909731890957245926915280713988801182894888947956846369966245947852409172099018409057129584780443712258590591272371802134906914886744538889099861890573943377480028655951935894660286388060056770675084677768397
c0 = 66400441793466385558399002350812383744096354576421495899465166492721568297592616443643465864544107914461044325088868615645524260480104397769130582397209585192620565774001015221725536884170662700337565613181799442382460047295553807602785067421981837709831158111951991854109179278733629950271657405211417740374
e1 = 62005504700456859456675572895620453845623573672275890584145949847469951381521709553504593023003977393014834639251022203398533914340078480147377747715528821418445514563871411209895815634752533151145061594791024551625615960423026244560340983481137777162236719939420428613005457949228517914830194749293637917667
n1 = 89410873947410184231222334229470195622685051370058935269198780539059522679122059486414591834635266301335656798768270022060656655274640699951736588085471509424575027153387518893978494158981314217195561629375189515702124478687925014362857206223379284909134299260355456357407022417434961226383007916607728238843
c1 = 75133250536426006056029454024900058936095761927174304108454764308417889983571094946046507426319589437822458959089546795698076608690695326741772662156830944126301658579142020817338297043884836598263468494533324693019866746045910394812656639124276516075062088756043949581789436307373276242558429450971458945061
e2 = 5365316217065391632204029784515519544882379449147835081003675696051077792179684123668298103660153980837519314114793091112163153158510344440829742753002176560016265852613076363394396640641504813912550948776926622696268531691467015580417575287779607009068332802842890478748171958455354463809356050553832863427
n2 = 53325942266099921615667538877103327425435396909592382386684073177331528393295928518724880712900970020425481561110366696624090824641115147978830715508666547064446891727446073538022824237798568413003419382767587742032676311751819789672319289920011033523044026418650515529084031754775286163358926609712626506433
c2 = 22289960513520782629306709529908652726794465066357062923684089176607114605563538085483920152508469429311012652149406853144200001391310165612163442404181970125704785325670969551080086517236489885046039799676581310781945432599048686184762485374030278657826206433571162451649808912276118945302558580745346371321
e3 = 57257245945110486431680573908783487217316546039634811903637650579658516537372808464426294780698320301497615457264001148504941375058983426920721566040576604013497311914160175024860226623138659970105781812246471618831032554729317463745699993647224910498474869868186318188994237457335796911524629938029123055027
n3 = 97233843381238063550322854422952777734101562842513647224354265328843953949189054347560960321126304504554067163501318212533606313039536188796999575130115659250566231010092273206623114900781284076452654791214088764465615154940874231056251107863895697778665275804663487113266180838319536762473697586368100928379
c3 = 56606672064789484727896188434430896229911224588055894584797861263107870392831242138537980507537270618683458635389444257040355313948352917061971042629958646854593628522401074068536976581232979947149230764268377747754284783531803366391759725774562719884482404532619163798580872386794273190532863916038929461465
'''
  • 这个就不赘述了，就是与推导的过程一样的，用我后面写的板子就可以一把梭了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
import gmpy2
import math
import time
from Crypto.Util.number import *

def know_phi_factor(n,phi):
    """
    已知phi分解n,仅限两个素数,n=pq
    参数n: 传入的是已知的n
    参数phi: 传入的是已知的phi
    返回值: (p,q)
    """
    b = phi - n - 1
    delta = b^2 - 4*n
    if delta < 0:
        return False
    p,q = var('p,q')
    eq1 = p*q == n
    eq2 = p^2 + (phi-n-1)*p+n == 0
    result = solve([eq1,eq2],p,q)
    p = int(result[0][0].rhs())
    q = int(result[0][1].rhs())
    if p*q == n:
        return (p,q)
    else:
        return False




def Common_Private_attack(n,e,debug):
    """
    参数1：n传入的是模数N构成的列表
    参数2：e传入的是模数N对应的公钥指数构成的列表
    参数3: 是否要调试这个程序
    """

    # 先对N进行排序操作,按照从小到大的顺序进行排序
    length = len(n)
    sort_n = n.copy()
    sort_n.sort()
    sort_e = [0] * len(e)
    
    if debug:
        print("[*]模数n排序前:",n)
        print("[*]模数n排序后:",sort_n)
        print()
        
    # 接下来根据排序的n对相应的公钥指数进行排序
    # 公钥指数就不是从小到大排序了,而是每个公钥指数要对应正确的模数
    for i in range(length):
        for j in range(length):
            if sort_n[i] == n[j]:
                sort_e[i] = e[j]
    if debug:
        print("[*]公钥指数排序前:",e)
        print("[*]公钥指数排序后:",sort_e)
        print()
        
    # 接下来计算 M = sqrt(N_max)
    M = gmpy2.iroot(sort_n[-1],2)[0]

    if debug:
        print("[*]计算得到M:",M)
        print()

    # 接下来开始造格,构成基矩阵
    base_matrix = Matrix(ZZ,len(n)+1,len(n)+1)
    base_matrix[0,0] = M
    for i in range(length):
        base_matrix[0,i+1] = sort_e[i]
        base_matrix[i+1,i+1] = -sort_n[i]
        
    if debug:
        print("[*]构造出来的基矩阵:")
        print(base_matrix)
        print()
        
    # 进行格基规约操作
    L = base_matrix.LLL()
    
    if debug:
        print("[*]规约后的基向量")
        print(L)
        print()

    # 由于最短向量可能不会出现在第一行,可能出现在后面几行
    # 接下来进行遍历这些向量,找到符合条件的最短向量
    for i in range(length+1):
        
        # 计算出对应的的d
        d = abs(L[i,0])//M
        
        # 接下来计算k,只计算一组,判断是否能分解成功
        if L[i,1] > 0:
            t = -L[i,1]
        else:
            t = L[i,1]
        
        k = (sort_e[0]*d - t)//sort_n[0]
        # 计算出k后再计算phi
        phi = (sort_e[0]*d-1)//k
        # 进行分解操作
        result = know_phi_factor(sort_n[0],phi)
        # 设置标志位,判断是否分解成功
        sign = 1
        if result == False:
            sign = 0

        # 标志位是1的话,将全部都分解掉
        if sign:
            p = []
            q = []
            p.append(result[0])
            q.append(result[1])
            for j in range(1,length):
                if L[i,j+1] > 0:
                    t = -L[i,j+1]
                else:
                    t = L[i,j+1]
                k = (sort_e[j]*d - t)//sort_n[j]
                phi = (sort_e[j]*d-1)//k
                result = know_phi_factor(sort_n[j],phi)
                p.append(result[0])
                q.append(result[1])
            if debug:
                print("分解成功")
                print("p列表如下")
                print(p)
                print("q列表如下")
                print(q)
                print("私钥d:d=",d)
                print("对应的n如下")
                print(sort_n)
                print("对应的e如下")
                print(sort_e)
                print()
            return (p,q,sort_n,sort_e,d)
        
        if debug:
            print(f"[*]第{i}行向量",L[i])
            print(f"[*]第{i}行向量对应的私钥指数候选d:",d)
            print(f"[*]第{i}行向量对应的候选值k:",k)
            print(f"[*]第{i}行向量对应的候选值phi:",phi)
            if sign:
                print(f"[*]第{i}行向量能分解出n")
            else:
                print(f"[*]第{i}行向量不能分解出n")
            print()
    return False
    

def example():
    # 设置debug:
    debug = False
    # 使用该脚本仅需要修改n和e:
    e0 = 
    n0 = 
    c0 = 
    e1 = 
    n1 = 
    c1 = 
    e2 = 
    n2 = 
    c2 = 
    e3 = 
    n3 = 
    c3 = 
    
    
    n = [n0,n1,n2,n3]
    e = [e0,e1,e2,e3]
    c = [c0,c1,c2,c3]
    if debug:
        print ("=== running algorithm ===")
        start_time = time.time()
        
    x = Common_Private_attack(n,e,debug)
    if x == False:
        print('[*]分解失败')
    else: 
        print('[*]分解成功')
        print('[*]对应p列表: p =',x[0])
        print('[*]对应q列表: q =',x[1])
        print('[*]对应n列表: n =',x[2])
        print('[*]对应公钥列表: e =',x[3])
        print('[*]对应公共私钥: d =',x[4])
        phi = (x[0][0]-1)*(x[0][0]-1)
        d = x[4]
        for i in c:
            m = pow(i,d,x[2][0])
            print(long_to_bytes(m))
    if debug:
        print("=== %s seconds ===" % (time.time() - start_time))
    
if __name__ == "__main__":
    example()
"""
b"\x0b\r\xd4\xd1\x97\xc7'\xe9\x81o`3\xb7<2D\xfd\xd7c\xbej1\x8c\x1f\x02y\xee\xbf\xd4\xfa\x1a*\xcb\xa9\xe7b\xcb\xfd\xd9\xf8i4\x1bA\xdd9u}\xc5\xf2\x9b{\xfb\x84\x1c|s1\xfd\x1a\xe0\x9b\t\xbch\xad\xcb\xcc\xfaTJsK\xfa\xc2R\xf4\xae\x1f(\xccG\x91_\x8c\xa4\x11z\x12l\x8c\x1f7\x1d1\x96m-\xd6\x94\x1d\xb2\xd1\xc2/\xbd\xcb\x9bx\x0e\x12\x0b\xeb5\xa5\xdf[<,-\xb9\x9e\xc8\xd85\x98\xc9\xaa"
b'\x13\x15h\x01\xb18\xe28n\xe0O\xec\xab\x87\x96\xdd\xb7\x95EXh\x97h\xe6\xfc\x96}\xe2\xcfO\x08\x058Q[\xd7+}*\xac\x83pd\xf1\xbd\xfaR\xc7\xd5\x13.0>\x05"\xcd\xdb7\xf25\xd5\xa1\x97\x1d\xd5\x85V:\x19\x0c\x147$\x8b\x93=\xaf\x01\xa5\x01\xf9\x0c\x1d\x06\xf4z\x02w\x13\xce\x15\xfeG\xd6\xe8;\xe06z\x88\\\xd7u\x81\xcc\xbb>\xf9\xac\xc4A;\xfa\xc6\xa9\x05+\x16\xd3D\xc3\x8a^gi\xdejN'
b'NSSCTF{12514adb-2c14-4777-96ff-90e95bc2b5cb}'
b'.u\xff\xea\xef\xdb\x0c\x8e\xc4}t\xe5|\x93\x9e\xd3\xc1\xc8\xa36\xa9H\x9c\xc2\xb7\xd0v>\x10\xfdJ\xea\xc3\xe1\xa3\xf0\x9fO\xbe\xe4\xc5\xcc\x8d\xcbB\x1fik\xbe\xd4\xfc}t\x8ak\x12\xc1\xcc\xa0\xb8\xb5\x01\xfc\xc8\xc4\x0b\xef<\xe5f8^p_%\x1d\xb5%\t\xa7s\x80!\x8bc\x0bG\xcf;MF\xf2\x15\xef\x07\x97\xdb~\x83\xfa\xec\x01G\x7f,\xef\xa9\xf9\xacb#\xf4M\xb5\xaaY\xcf\xc8\x9a\xa3\xb2Bvtf\x83\xff\x0e'
"""

共私钥攻击 板子

  • 自己写了一个板子：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
import gmpy2
import math
import time


def know_phi_factor(n,phi):
    """
    已知phi分解n,仅限两个素数,n=pq
    参数n: 传入的是已知的n
    参数phi: 传入的是已知的phi
    返回值: (p,q)
    """
    b = phi - n - 1
    delta = b^2 - 4*n
    if delta < 0:
        return False
    p,q = var('p,q')
    eq1 = p*q == n
    eq2 = p^2 + (phi-n-1)*p+n == 0
    result = solve([eq1,eq2],p,q)
    p = int(result[0][0].rhs())
    q = int(result[0][1].rhs())
    if p*q == n:
        return (p,q)
    else:
        return False




def Common_Private_attack(n,e,debug):
    """
    参数1：n传入的是模数N构成的列表
    参数2：e传入的是模数N对应的公钥指数构成的列表
    参数3: 是否要调试这个程序
    """

    # 先对N进行排序操作,按照从小到大的顺序进行排序
    length = len(n)
    sort_n = n.copy()
    sort_n.sort()
    sort_e = [0] * len(e)
    
    if debug:
        print("[*]模数n排序前:",n)
        print("[*]模数n排序后:",sort_n)
        print()
        
    # 接下来根据排序的n对相应的公钥指数进行排序
    # 公钥指数就不是从小到大排序了,而是每个公钥指数要对应正确的模数
    for i in range(length):
        for j in range(length):
            if sort_n[i] == n[j]:
                sort_e[i] = e[j]
    if debug:
        print("[*]公钥指数排序前:",e)
        print("[*]公钥指数排序后:",sort_e)
        print()
        
    # 接下来计算 M = sqrt(N_max)
    M = gmpy2.iroot(sort_n[-1],2)[0]

    if debug:
        print("[*]计算得到M:",M)
        print()

    # 接下来开始造格,构成基矩阵
    base_matrix = Matrix(ZZ,len(n)+1,len(n)+1)
    base_matrix[0,0] = M
    for i in range(length):
        base_matrix[0,i+1] = sort_e[i]
        base_matrix[i+1,i+1] = -sort_n[i]
        
    if debug:
        print("[*]构造出来的基矩阵:")
        print(base_matrix)
        print()
        
    # 进行格基规约操作
    L = base_matrix.LLL()
    
    if debug:
        print("[*]规约后的基向量")
        print(L)
        print()

    # 由于最短向量可能不会出现在第一行,可能出现在后面几行
    # 接下来进行遍历这些向量,找到符合条件的最短向量
    for i in range(length+1):
        
        # 计算出对应的的d
        d = abs(L[i,0])//M
        
        # 接下来计算k,只计算一组,判断是否能分解成功
        if L[i,1] > 0:
            t = -L[i,1]
        else:
            t = L[i,1]
        
        k = (sort_e[0]*d - t)//sort_n[0]
        # 计算出k后再计算phi
        phi = (sort_e[0]*d-1)//k
        # 进行分解操作
        result = know_phi_factor(sort_n[0],phi)
        # 设置标志位,判断是否分解成功
        sign = 1
        if result == False:
            sign = 0

        # 标志位是1的话,将全部都分解掉
        if sign:
            p = []
            q = []
            p.append(result[0])
            q.append(result[1])
            for j in range(1,length):
                if L[i,j+1] > 0:
                    t = -L[i,j+1]
                else:
                    t = L[i,j+1]
                k = (sort_e[j]*d - t)//sort_n[j]
                phi = (sort_e[j]*d-1)//k
                result = know_phi_factor(sort_n[j],phi)
                p.append(result[0])
                q.append(result[1])
            
            print("分解成功")
            print("p列表如下")
            print(p)
            print("q列表如下")
            print(q)
            print("私钥d:d=",d)
            print("对应的n如下")
            print(sort_n)
            print("对应的e如下")
            print(sort_e)
            print()
            return (p,q,sort_n,sort_e,d)
        	
        if debug:
            print(f"[*]第{i}行向量",L[i])
            print(f"[*]第{i}行向量对应的私钥指数候选d:",d)
            print(f"[*]第{i}行向量对应的候选值k:",k)
            print(f"[*]第{i}行向量对应的候选值phi:",phi)
            if sign:
                print(f"[*]第{i}行向量能分解出n")
            else:
                print(f"[*]第{i}行向量不能分解出n")
            print()
    return False
    

def example():
    # 设置debug:
    debug = True
    # 使用该脚本仅需要修改n和e:
    n = [2915050561,3863354647,3943138939]
    e = [587438623,2382816879,2401927159]
    if debug:
        print ("=== running algorithm ===")
        start_time = time.time()
        
    x = Common_Private_attack(n,e,debug)
    if x == False:
        print('[*]分解失败')
    else: 
        print('[*]分解成功')
        print('[*]对应p列表: p =',x[0])
        print('[*]对应q列表: q =',x[1])
        print('[*]对应n列表: n =',x[2])
        print('[*]对应公钥列表: e =',x[3])
        print('[*]对应公共私钥: d =',x[4])
    if debug:
        print("=== %s seconds ===" % (time.time() - start_time))
if __name__ == "__main__":
    example()

共私钥攻击 实际效果

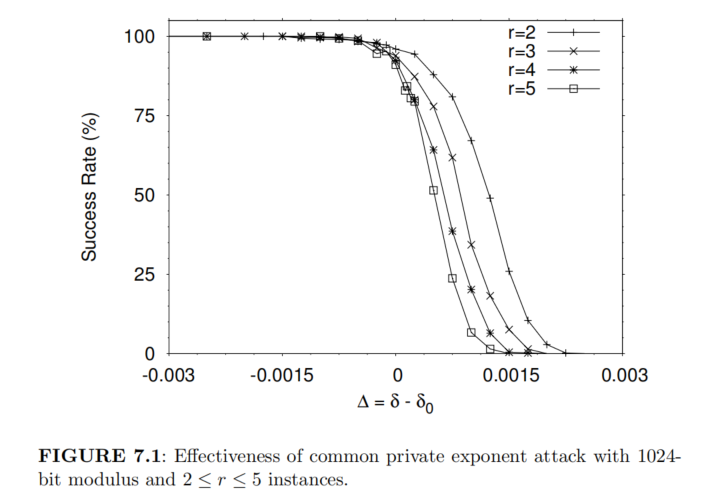
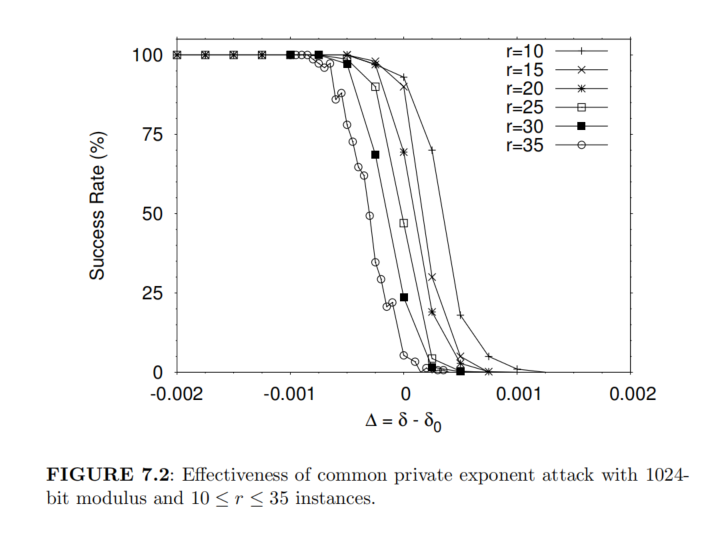
  • 共私钥攻击仅仅是启发式的，它的正确价值在于它在实践中的有效性。在图7.1中和7.2中，展示了这样一种攻击效率：在1024位模数的随机RSA实例中，多个不同模数共享同一个较小的私钥指数，其中参数范围为2≤r≤352≤r≤35，成功率以Δ=δ−δr\Delta=\delta-\delta_r为自变量给出，其中δ\delta表示私钥指数的大小，而δr=12−12(r+1)−logNr(6)\delta_r = \frac{1}{2}-\frac{1}{2(r+1)}-log_{N_r}(6)是攻击中给出的界限。
  • 当Δ<0\Delta<0时，对应于私钥指数小于δr\delta_r的情况；当Δ>0\Delta > 0时，则对应于私钥指数大于δr\delta_r的情况。图中的每一个数据点表示在若干次独立随机实例上重复实验后得到的平均成功率。
  • 对于每个数据点，实验次数r=2r=2时的1500次此时格基规约所花费的时间很短，到r=35r=35时的150次（此时规约时间显著增加）。
  • 从图7.1和图7.2的数据可以看出如下规律：
    • 在Δ≈0\Delta\approx 0之前，该攻击的效果非常理想，接近完美。
    • 一旦Δ≈0\Delta\approx 0，攻击的成功率便迅速下降，以及趋近于0。
    • 随着实例数量的增加（即rr的增大），当Δ\Delta接近或大于0时，攻击有效性的下降趋势显得更加明显
    • 与实例无关的是，在所有实验中，当Δ<−0.0025\Delta < -0.0025时，攻击均能够成功。
    • 基于这些实验结果，可以认为：格中的假设，对共私钥攻击所使用的格是成立的，并且该攻击在实践中使用1024位模数的多实例RSA具有良好效果。

image-20260213002235787

image-20260213002247368

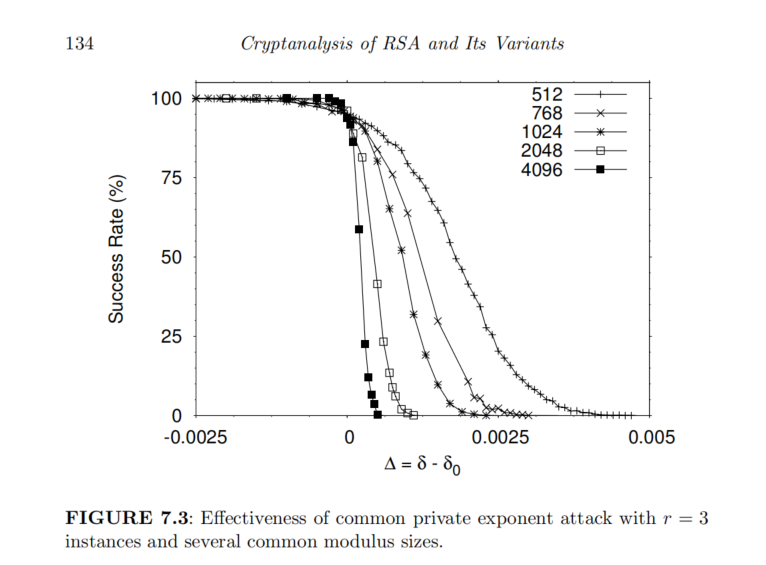
  • 下图7.3，我们展示了当三个RSA实例共享同一个较小的私钥指数即r=3r=3时，该攻击在不同模数位数下的有效性。
    • 从实验数据构成的图表可以看出，对于所考虑的每一种模数规模，该攻击都保持了较高的有效性。
    • 随着模数位数的增加，成功攻击与攻击失败之间的临界点切换变得更加陡峭，其形态似乎逐渐趋近于阶跃函数
    • 图中的每个数据点均表示在1500次实验中得到的平均攻击成功率，基于这些实验结果，可以明确的认为：对于模数位数介于512~4096位之间、且存在三个实例共享小私钥指数的RSA，该共私钥攻击在实践中有非常好的效果。

image-20260213002957459