• 这个比赛密码题难度比较简单，pwn题难度偏难，有涉及到SMM、UEFI、BootKit。可以花时间学一学这些如何PWN。不过先把密码复现了。

Crypto

the shortest crypto chal*

  • 自己想没想出来，看wp吧。

  • 题目附件：

1
2
3
4
5
6
7
8
from Crypto.Cipher import AES
from hashlib import md5
from secret import a,b,c,d, FLAG

assert a**4 + b**4 == c**4 + d**4 + 17 \
       and max(a,b,c,d) < 2e4 \
       and AES.new( f"{a*b*c*d}".zfill(16).encode() , AES.MODE_ECB).encrypt(FLAG).hex() == "41593455378fed8c3bd344827a193bde7ec2044a3f7a3ca6fb77448e9de55155"

  • 这题算是一个类似于小游戏，并且题目中已经给出max(a,b,c,d) < 2e4，这样其实就可以确定a,b,c,d < 20000，但是如果要单纯爆破的话还是不太行。
  • 我们不妨考虑一下对这个等式做因式分解，但是发现分解不出来什么东西：
1
2
3
4
5
6
PR.<a,b,c,d> = PolynomialRing(ZZ)
f = a^4 + b^4 - c^4 - d^4 -17
f.factor()
"""
(-1) * (-a^4 - b^4 + c^4 + d^4 + 17)
"""
  • 那接下来就要考虑其他东西了，接下来我们考虑这个式子：

$$
\begin{array}{l}
a^{4}-c^{4}+b^4 - d^{4} = 17\
(a^2+c^2)(a^{2}-c^{2})+(b^{2}+d^{2})(b^{2}-d^{2})=17\
(a^2+c^2)(a+c)(a-c)+(b^2+d^{2})(b+d)(b-d)=17
\end{array}
$$

  • 那么就有：

$$
\begin{array}{l}
a^4-c^4+b^{4}-d^4>0\
a^4-c^4>d^4-b^4\
a-c>d-b\
a+b>d+c
\end{array}
$$

  • 其实还可以确定以下两种可能：
    • 可能性1：$a-c>0$且$b-d<0$
    • 可能性2：$a-c < 0$且$b-d>0$
  • 继续推：

$$
\begin{array}{l}
a^4+b^4 ≥2a^2b^2\
c^4+d^4+17≥2a^2b^2
\end{array}
$$

  • 逆推过去：

$$
t = abcd
$$

too many primes

  • 题目附件如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from sympy import nextprime, randprime
from sympy.core.random import seed
from math import prod, gcd
from Crypto.Util.number import bytes_to_long
# from secret import phi_N, FLAG

p = randprime(2**127, 2**128)
N = 1
while N < 2**2048:
	N *= p
	p = nextprime(p)

assert gcd(phi_N, 65537) == 1

pt = bytes_to_long(FLAG)
ct = pow(pt, 65537, N)
print("N = ", N)
print("ct = ", ct)
# N =  34546497157207880069779144631831207265231460152307441189118439470134817451040294541962595051467936974790601780839436065863454184794926578999811185968827621504669046850175311261350438632559611677118618395111752688984295293397503841637367784035822653287838715174342087466343269494566788538464938933299114092019991832564114273938460700654437085781899023664719672163757553413657400329448277666114244272477880443449956274432819386599220473627937756892769036756739782458027074917177880632030971535617166334834428052274726261358463237730801653954955468059535321422372540832976374412080012294606011959366354423175476529937084540290714443009720519542526593306377
# ct =  32130352215164271133656346574994403191937804418876038099987899285740425918388836116548661879290345302496993945260385667068119439335225069147290926613613587179935141225832632053477195949276266017803704033127818390923119631817988517430076207710598936487746774260037498876812355794218544860496013734298330171440331211616461602762715807324092281416443801588831683678783343566735253424635251726943301306358608040892601269751843002396424155187122218294625157913902839943220894690617817051114073999655942113004066418001260441287880247349603218620539692362737971711719433735307458772641705989685797383263412327068222383880346012169152962953918108171850055943194

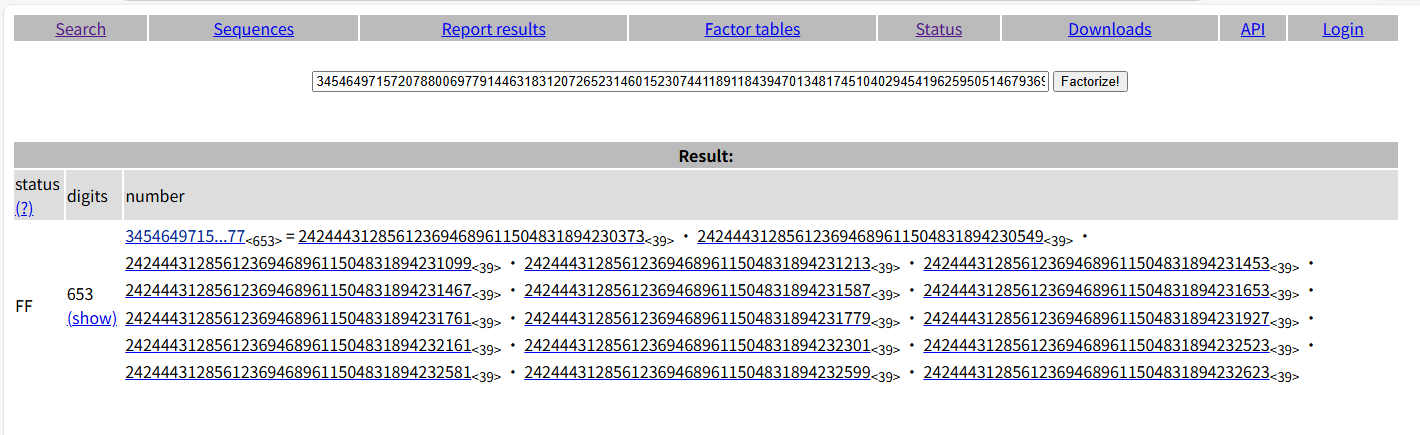
  • 这题是RSA变种之一，多素数RSA加密的分解N的题，这题可以直接factordb.com分解出来

image-20260215210303461

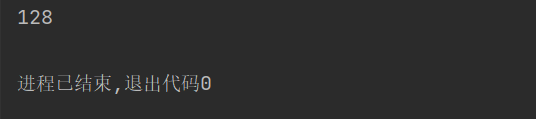
  • 这题还有一个方法，就是费马分解法，先确定到底有多少个128位的素数相乘，爆破一下，发现是17个素数相乘，因为开17次方后的结果就可以得到128字节的一个数。
1
2
a = gmpy2.iroot(N,17)[0]
print(int(a).bit_length())

image-20260215210455770

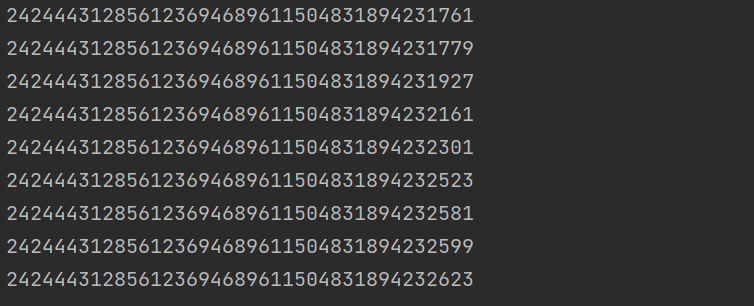
  • 此时只要利用费马分解的思想，就可以稍微爆破出大于N开17次方的素数，发现有9个素数已经被找到了

image-20260215210550114

1
2
3
4
5
6
7
8
9
10
11
12
N = 
a = gmpy2.iroot(N,17)[0]
p = []
while True:

    x = N % a
    if x == 0:
        p.append(int(a))
        print(p)
        N = N//a
    a = a + 1
  • 接下来就是用sympy库中的prevprime，求解出钱8个素数。就可以解密了。
  • exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import gmpy2
from sympy import nextprime, randprime, prevprime
from Crypto.Util.number import bytes_to_long, inverse , long_to_bytes
N = 
ct = 
e = 65537
a = gmpy2.iroot(N,17)[0]
p = [242444312856123694689611504831894231761, 242444312856123694689611504831894231779, 242444312856123694689611504831894231927, 242444312856123694689611504831894232161, 242444312856123694689611504831894232301, 242444312856123694689611504831894232523, 242444312856123694689611504831894232581, 242444312856123694689611504831894232599, 242444312856123694689611504831894232623]
q = p[0]
for i in range(17-len(p)):
    q = prevprime(q)
    p.append(q)

phi = 1
for i in p:
    phi = phi * (i-1)
d = inverse(e,phi)
m = pow(ct,d,N)
flag = long_to_bytes(m)
print(flag)
"""
b'uiuctf{D0nt_U5e_Cons3cUt1vE_PriMeS}'
"""

back to roots

  • 题目附件如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from random import randint
from decimal import Decimal, getcontext
from hashlib import md5

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad

from secret import FLAG

K = randint(10**10, 10**11)
print('K', K)
leak = int( str( Decimal(K).sqrt() ).split('.')[-1] )

print(f"leak = {leak}")
ct = AES.new(
	md5(f"{K}".encode()).digest(),
	AES.MODE_ECB
).encrypt(pad(FLAG, 16))

print(f"ct = {ct.hex()}")
"""
leak = 4336282047950153046404
ct = 7863c63a4bb2c782eb67f32928a1deceaee0259d096b192976615fba644558b2ef62e48740f7f28da587846a81697745
"""
  • 此题考察的就是Decimal这个东西，Decimal算是一个精度保存的东西。
    • 首先就是随机选取一个值K，然后对这个K值转换为Decimal精度存储。
    • 之后就是对精度存储的这个K值进行开根，开根后会保存小数点。
    • 而题目中的leak，泄露的就是开根后的小数点部分。
  • 经过测试，randint(10**10,10**11)开根后的整数范围大概在randint(10**5,10**6)的范围就行了。所以只需要爆破就行
  • 具体的exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from random import randint
from decimal import Decimal, getcontext
from hashlib import md5
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import tqdm
ct = '7863c63a4bb2c782eb67f32928a1deceaee0259d096b192976615fba644558b2ef62e48740f7f28da587846a81697745'
r = '0.4336282047950153046404'
s = Decimal(r)
for i in tqdm.tqdm(range(10^5,10^6),leave=True):
    k = str(int((Decimal(i)+s)^2))
    ci = AES.new(md5(k.encode()).digest(),AES.MODE_ECB)
    flag = ci.decrypt(bytes.fromhex(ct))
    if b'ctf' in flag:
        print(flag)
        
"""
b'uiuctf{SQu4Re_Ro0T5_AR3nT_R4nD0M}\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f\x0f'
"""

symmetric

  • 题目附件如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
from secret import FLAG

p, q, r, s = [getPrime(512) for _ in "1234"]

print(f"h1 = {p + q + r + s}")
print(f"h2 = {p**2 + q**2 + r**2 + s**2}")
print(f"h3 = {p**3 + q**3 + r**3 + s**3}")

N = p*q*r*s
print(f"N = {N}")
pt = bytes_to_long(FLAG)
ct = pow(pt, 65537, N)
print(f"ct = {ct}")

"""
h1 = 44626154099651354925697068610752642661842459492769931945027538340211738148995902544351457443643808803963130274930824732652561687395268828472477422919262224
h2 = 516671113554555861164166966331322883848052630063409185414998284127910160310316421085219788291486248715029393774584960034375836715001130337767354512063372620828300201147366138270597133744747341658011663632381219284289144790858167258162656417236910634201286428763727072739569460623482985066956478781223378673732
h3 = 6147718474663450187001867904227777991349731066494841442199681943204194617136760567222545181562592364728655444222576167723225771866335920325045525027985716792468801076590684892140052786942251780392395274059384743594570343510311801194684613435002073956759521242578078411431891501758484581445964234548107005826532945720412531638919892681259687552977883437895032963223761216846303917338652743754915155934118353066174102436448393348040719582422022713292561416343278608
N = 14184841414933523698606245433393907034474143715949896731683874356940146602876788990832087413915033843120975580859113356518777762025417525571528638829956003882418585702756644491932279294535883798799580861254646149745925137179207140600356428758736111639677698862407787386573263961111978517446397007747429416079059195916290615125084899002162504424765939524455434579218079962808920072946861658695379491917567048202142417165204141307476222251547098848515065051745905180788313450494477967398727631152936238366581978379130450660235139256967936160718128731512409111209840405772933034600016694225294481603355934917366484109057
ct = 720607330561370237459911161481490697044029472780348552630924063963226757984368356580217337982783395620115957442082471977614781910209933696251479615689667675958354681196823652299435457532944189300223816303315625302472302494905575910600277892375951366031061219173465155686586206246661009612156094695841741309002508535764511343569015518587247600796520847856011377777228749182958947015029731456117404560626347774985507275302882865400315045173501559082431672490227728580592379740508214726249635835834752208899970446910850569489282065524329936561486377823093465841715608716032843259935185417766702677708267102415636848129
"""
  • 此题还是一个多素数RSA的题型，这个题型还是分解模数类型的题型，但是这个题目中泄露的是：

$$
\begin{array}{l}
p+q+r+s=h_1\
p^2 + q^2 + r^2 + s^2=h_2\
p^3 + q^3 + r^3 + s^3=h_3
\end{array}
$$

  • 直接用sagemath解方程即可，因为算上h1、h2、h3、n恰好就是4个未知数，4个方程能求解出来。
  • exp如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
p,q,r,s = var('p,q,r,s')
h1 = 
h2 = 
h3 = 
N = 
ct = 
e = 65537
eq1 = p*q*r*s == N
eq2 = p+q+r+s == h1
eq3 = p^2 + q^2 + r^2 + s^2 == h2
eq4 = p^3 + q^3 + r^3 + s^3 == h3
result = solve([eq1,eq2,eq3,eq4],p,q,r,s)[0]
p = result[0].rhs()
q = result[1].rhs()
r = result[2].rhs()
s = result[3].rhs()
phi = (p-1)*(q-1)*(r-1)*(s-1)
d = inverse(e,phi)
m = pow(ct,d,N)
flag = long_to_bytes(int(m))
print(flag)
"""
b'uiuctf{5yMmeTRiC_P0lyS_FoRM_A_B4S15}'
"""

PWN