格理论初探
- 格理论在密码分析和破解这块是个好工具,而CTF又是偏向解题,在密码学这个方向中其实就是对加密过程和密文以及密钥进行密码分析,发现并破解其中潜在的漏洞。所以对于打CTF来说,格理论是不得不学的一个大方向,使用格能破解一些传统加密。
- 格理论除了在密码分析和破解这块起妙用之外,还基于格的几个困难问题设计了一些与格相关的加密(目前我还不知道加密的效率怎么样,有听别人说,但是自己没体会到。)
- 其实大二就很想入门格密码学,但是由于时间都花在
pwn上,有的时候不仅内耗,还比较浮躁,就导致效率比较低。不过现在大三感觉已经在密码学和pwn这两个方向上已经快突破我的平台期了。大二暑假的时候将初等数论学了个大概(还有指数与原根、连分数、超越数、丢番图,其实原本暑假还打算把抽象代数能学多少就学多少,可惜可惜)。目前有个这么打算高等代数和抽象代数学完,就来学代数数论和解析数论。
参考资料
-
对于格理论、格密码来说,国外的资料是一大堆的,国内的资料是真没多少。而国外资料又是
英文看一页都老半天了。所以在学习格之前,我就先做了点信息收集。 -
首先是王小云写的一篇论文:格密码学研究,这篇论文并不是学格相关的理论知识,当做看小说一样看一遍下来,对格的整个发展有一个比较清晰的脉络。还有就是该论文中引用比较多的论文,可以看看这些引用的论文。通过看该论文,可以大致了解一些格理论的一些专有名词,比如格的困难问题
CVP、SVP等,以及一些定理还有格与机器学习的交叉LWE问题。 -
目前找到的一本比较系统的写格理论与格密码的书籍了:
格理论与密码学 周福才,徐剑编著,这本数是中文的书籍,字还是可以看得比较顺畅的。 -
还有一本就是涵盖内容比较多的一本英文教材:
《COMPLEXITY OF LATTICE PROBLEMS A Cryptographic Perspective》Daniele Micciancio、Shafi Goldwasser著 -
国外还有一本书:
《AnIntroduction to Mathematical Cryptography》Jeffrey Hoffstein、Jill Pipher、Joseph H. Silverman -
接下来就是一些视频了,这个是英文视频:2012年BIU密码学冬令营-04-Basic Cryptanalysis(中文字幕)_哔哩哔哩_bilibili
-
这个是中文的一些教学视频:全同态加密理论: 格密码的数学基础
-
这个代数数论的视频也有讲一部分格,在第
125个视频中:经典代数数论2021 -
《数的几何引论》朱尧辰 -
参考博客:初识格 | DexterJie’Blog
格初步认识
格相关概念
- 这一部分主要简述一下通过阅读一些资料对格这个概念的一些初步认识。没啥图片都是文字。
- 格密码的发展大体分为两条主线:
- 一是从具有悠久历史的格经典数学问题的研究发展到近30多年来高维格困难问题的求解算法以及其计算复杂性理论研究
- 二是从使用格困难问题的求解算法分析非格公钥密码体制的安全性发展到基于格困难问题的密码体制的设计。
- 格的研究源于
1611年开普勒提出的如下猜想:在一个容器中堆放等半径的小球所能达到的最大密度为。 1840年前后,高斯引入了格的概念并证明了:在三维空间中堆球,如果所有的球心构成一个格,那么堆积密度所能达到知道最大值为。- 之后在过去的一个半世纪中,
Minkowski、Hermite、Bourgain、Hlawka、Kabatyansky、Levenstein、Lovasz、Mahler、Rogers等著名数学家系统地发展了一般几何体的格堆积与覆盖理论。在这一发展过程中,确定一个几何体的最大格堆积密度和最小格覆盖密度一直是这一个学科的核心问题。(对与格数学的这个发展过程全部都摘抄自王小云教授)。
首先来了解一下格的定义:格是中一类具有周期性结构的离散点的集合,严格地来说,格是m维欧式空间的个线性无关向量组的所有整系数线性组合即:
向量组称为格的一组基,同一个格可以用不同的格基表示,即存在使得,m称为格的维数,n称为格的秩。满足的格称为满秩的。通常研究都是研究满秩的格也就是
m=n这一情况。误区:对于格的定义来说,我们只规定了必须为整数,而向量中的数可以不是整数。而格点其实是格中的向量,由于基向量进行加加减减运算后还是一个向量,这个向量其实是可以用坐标表示的。其几何意义就是从
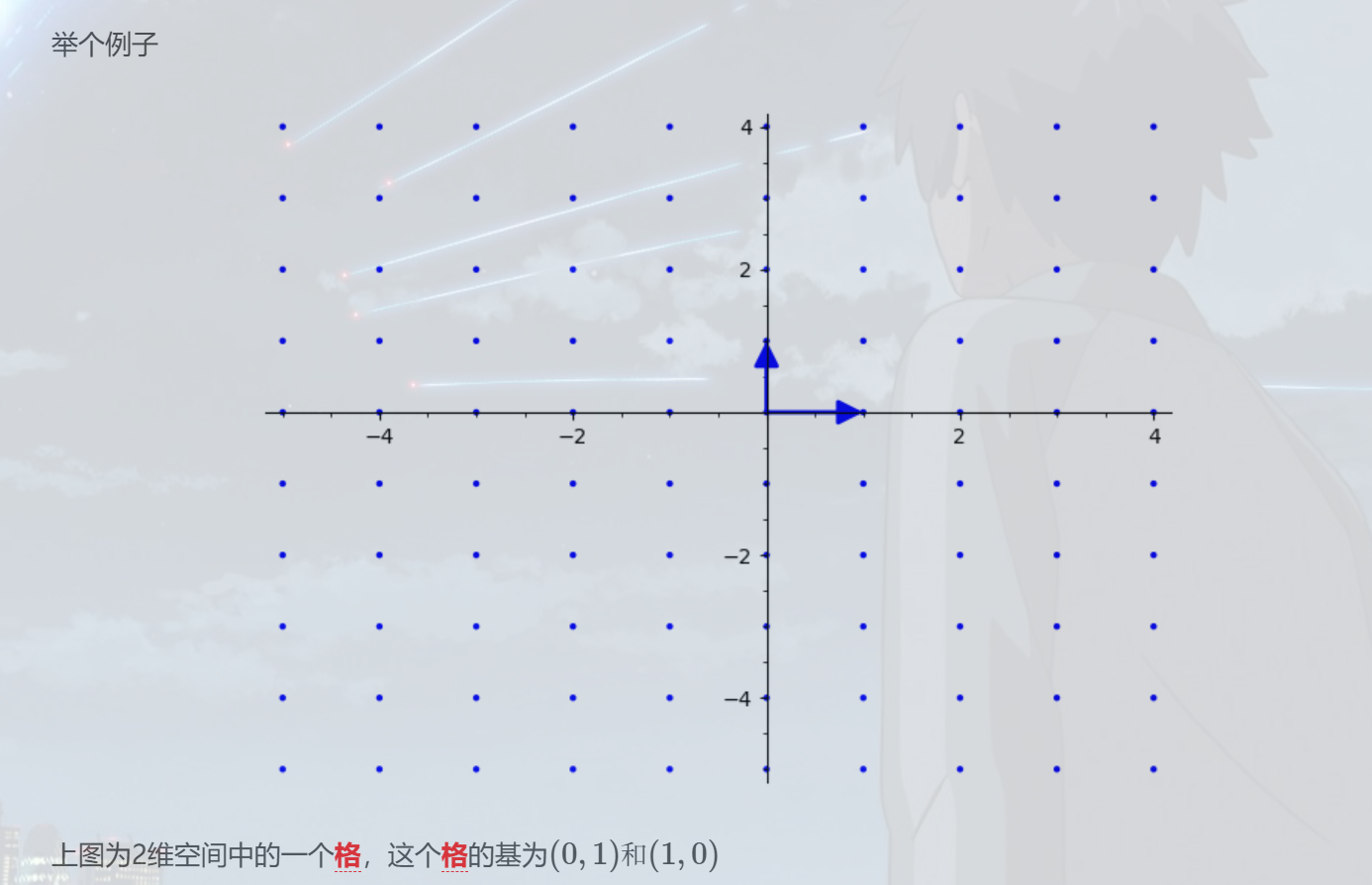
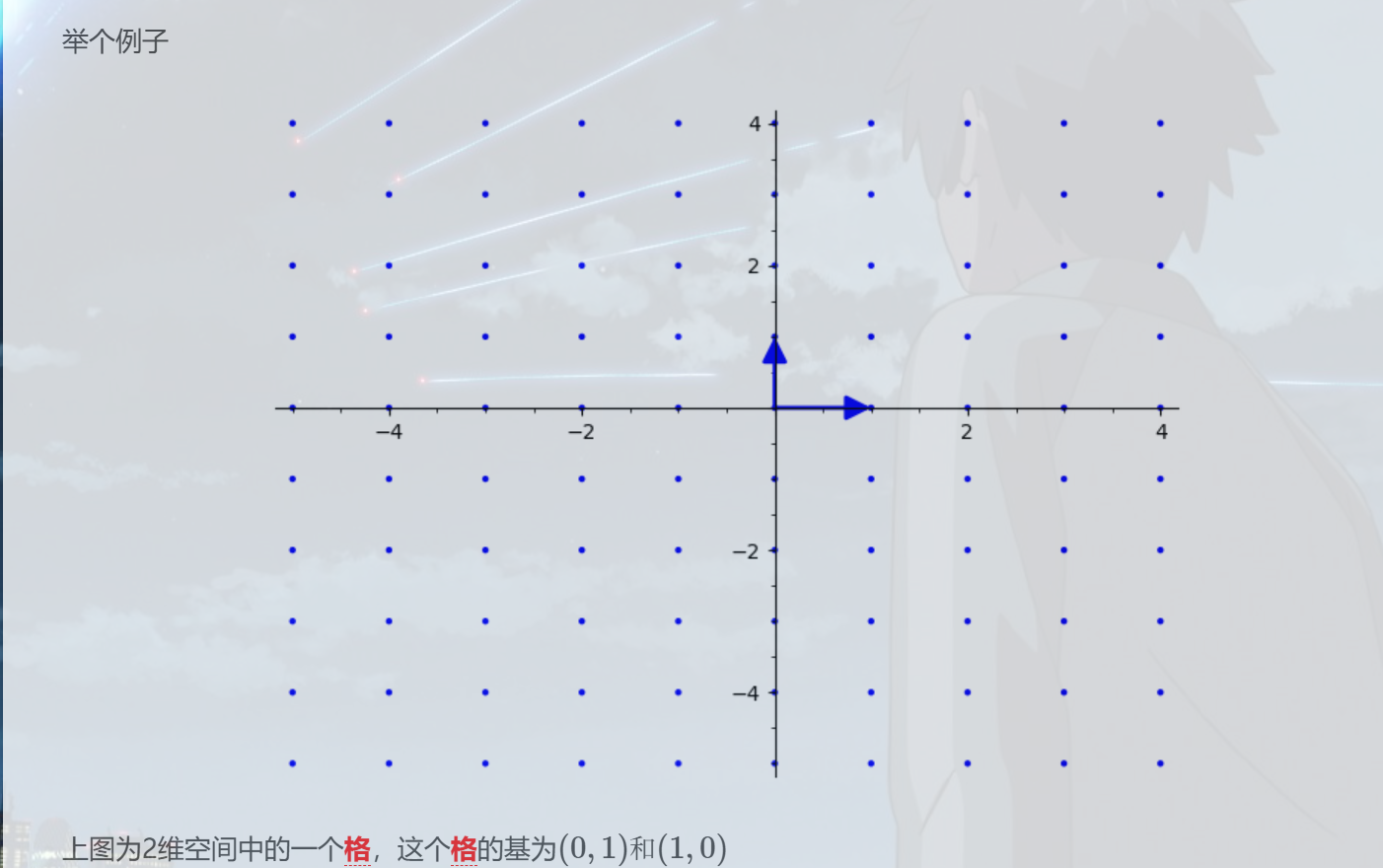
(0,0)通过这个向量指向坐标的一个点。所以格点其实是格向量对于格的定义来说,现在感觉还是很抽象,直接上图直接,对于格来说,其几何意义就是平面上、空间上离散而又规律的点。
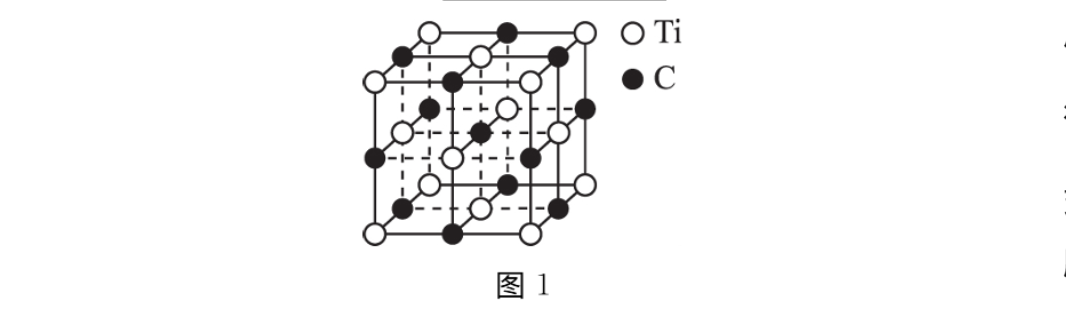
而在空间中,也是许许多多有规律的点,在高中化学物质结构中的一些晶体是由原子构成的,都是这么画的有固定,规律的原子排布。(这么一想量子计算机也是从原子等微观角度出发,格是从这些散点出发,二者好像似乎有点联系唉?)
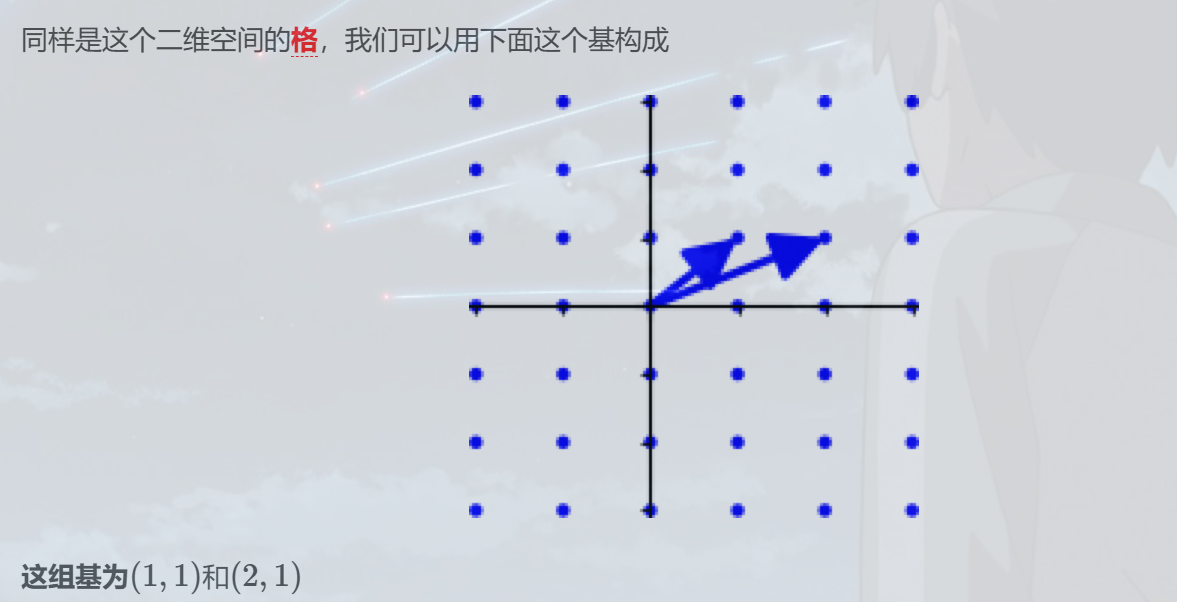
这里还需要注意:不同的格基,可能生成的是相同的格
注解1:从格的定义出发,如果认真学过线性代数就会发现,这个其实就是线性代数中向量空间基的表达方式。如果使用高中教材向量那一部分来说明的话那其实格的表达其实就相当于向量的一组基底表达。线性代数和高中所学的基底,线性代数的表达就不说了(大一线代没好好学都把时间花在学pwn那边了,所以现在回头再看高等代数。),而线代和高中所学的基底
x,y的取值范围都是在实数范围之内的,而格这个定义,说明向量前面的系数是整数。所以格才会是空间中离散的具有周期性的点的集合。注解2:从格的引入其实可以知道格与几何关系比较密切;从格的定义来说格又是由向量定义的,向量又与矩阵有关,所以格与线性代数、高等代数关系又非常密切;继续从格的定义来说,基底向量的系数都是整数又彻到整数了,那就和初等数论也扯上关系了。(不知道这算不算强行扯关系,按照自己的理解是这样的)。格与以上的数学分支与基础都有关系,那么绝对与抽象代数也很有关系的。
注解3:既然格与这么多数学分支有联系,那么这些数学分支中的某些定理都可以使用到格上。而从格的定义使用向量定义并且也可以使用矩阵表示,那么其实矩阵、向量、向量空间的一些性质都可以使用到格上。可以毫不客气地说学格之前先把线性代数学好或者高等代数学好。
通过对格的逐步了解,了解到了研究个一般研究满秩的格,这里还要做一点说明研究格的这一数学分支似乎被称为几何数论,数的几何引论,在2025.9.11找到了国内的一本书专门讲几何中的格,也就是传统意义上格用来研究的几何体堆叠问题《数的几何引论》朱尧辰
格的基本体(基胞):
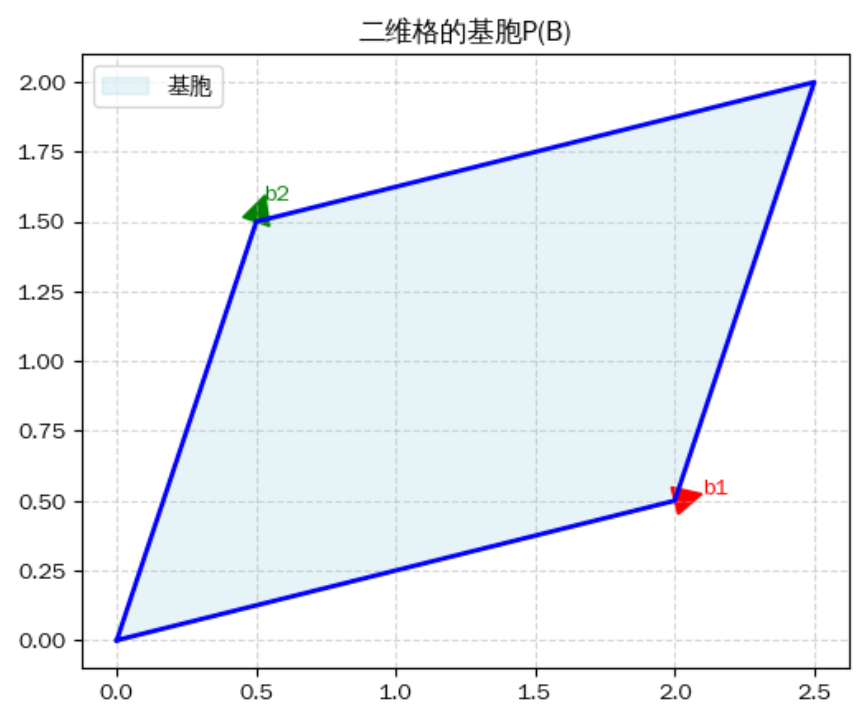
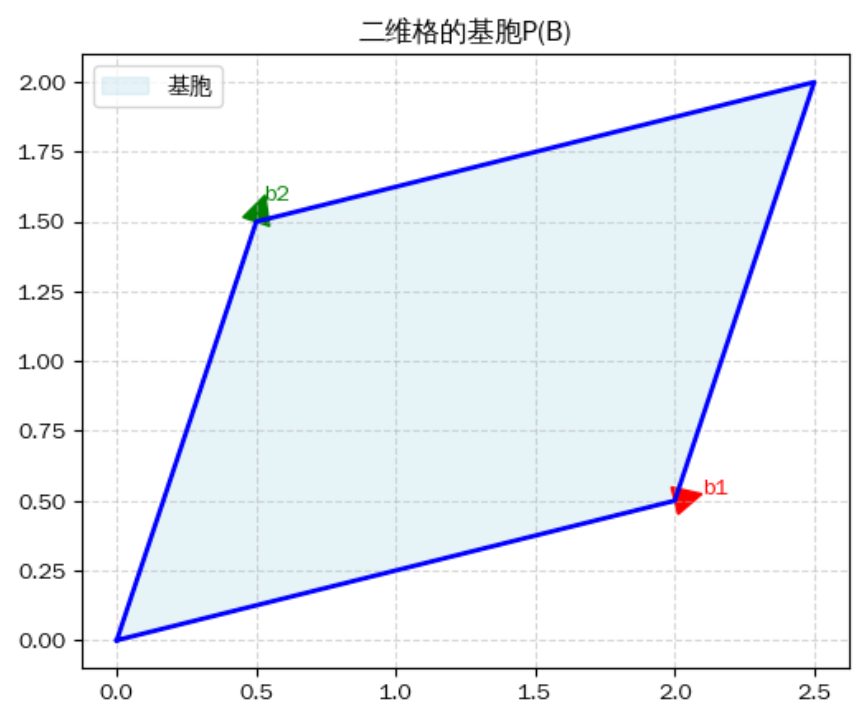
格的基本体是由格基向量生成、并作为在中代表每个同余类的一个原胞。若格由线性无关的基向量生成即,那么格的基本体则定义为:
误区:根据基胞的定义,是在
0~1任意取值的,这就说明,基胞是一个连续的区域,在二维上就是一个平面,在三维上其实就是一个立体图形。而格点或落在平面或者是立体图形的顶点上,并且图形内部是没有格点的。如图所示,基胞其实是平行四边形阴影那部分,而格是平行四边形的四个顶点。
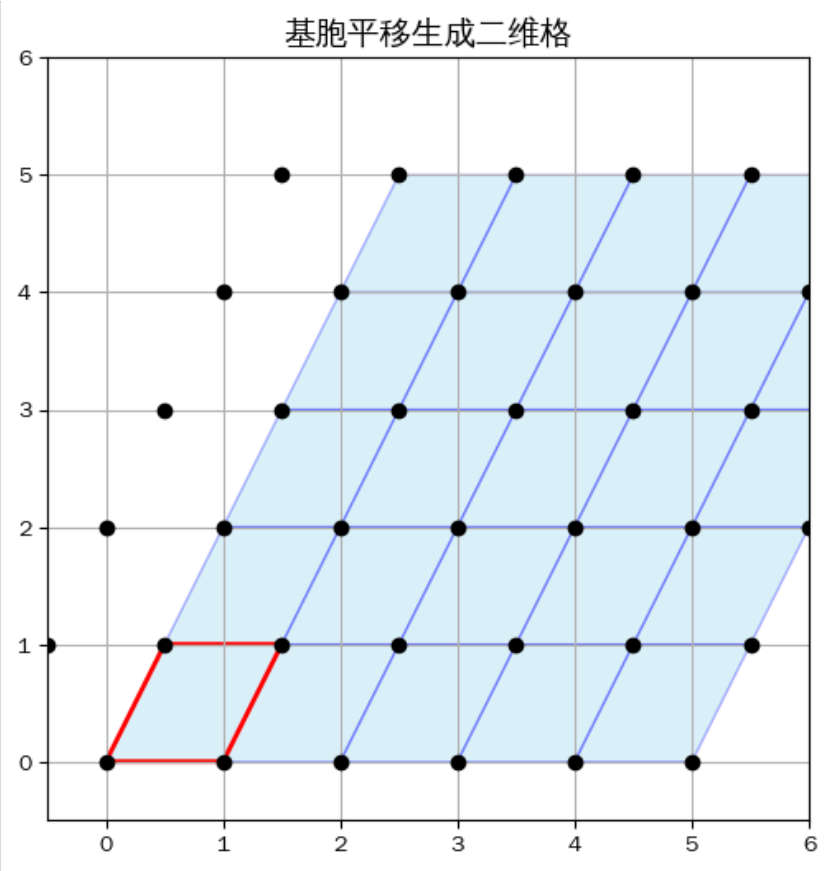
将基胞进行平移整数个单位长度,平行四边形的四个顶点也会被移动到不同的地方,从而构成格。
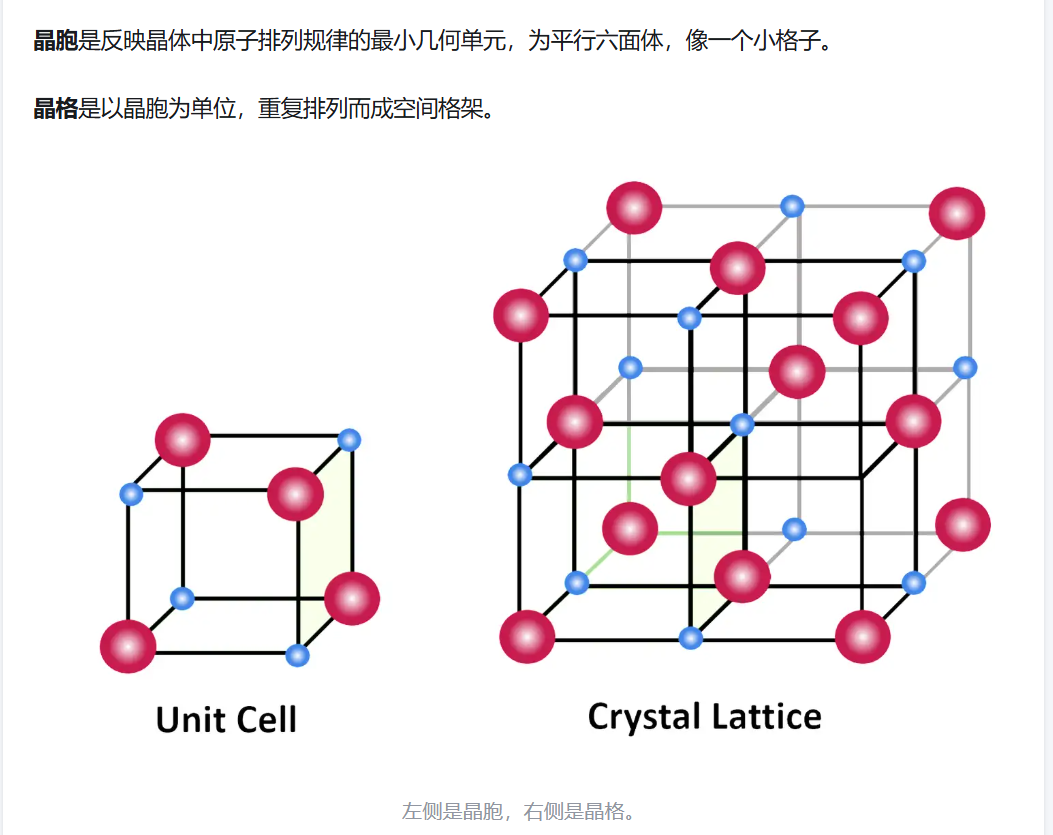
而到三维或者更高维的立体图形来说,其实可以用化学中物质结构进行类比。晶胞就相当于一个基胞,晶胞顶点上的原子就相当于格点,相同的基胞构成了晶格,而基胞平移会构成格。
由于研究的一般都是满秩格,而满秩格一般都会有行列式,接下来就需要介绍一下行列式对于格基本体来说的几何意义。
格的行列式的几何意义:
格的行列式的值定义为格基本体的有向面积或者说是有向体积。就比如下图,下图中,则的几何意义就是图中平行四边形的面积(但是带有正负号,具体正负要通过右手定则来判断。)
优质基与劣质基
- 给定一组基向量,它可以通过整数倍的加加减减,得到一个格。但是这个基有好坏之分的,如何定义这个基的好坏呢?通过研究就有如下评判基的好坏的标准:
一组基如果很容易能表示出格中所有的点,那么这组基就是优质基。
一组基如果表示出格中所有的点非常困难,那么这组基就是劣质基。
注解:由于格是由基的整数倍加加减减,而不是实数倍加加减减,这就导致了对于有些基来说,表示一个靠近原点的格点,都需要
10000000v+20000000u这么大的一个系数,也就是说有些格点非常难表示出来。
- 我们此时已经给优质基和劣质基下了一个定义,那么就我们就需要研究这两种基有什么特征(这样才能一看图片或者一把这一组基从图中画出来就能判断它是优质基还是劣质基了)。研究优质基和劣质基得到了如下特点:
劣质基具有的特点:
- 长度差异非常大:基向量有的长度非常长、有的长度又非常短
- 基向量夹角接近共线:基向量之间的夹角接近共线,可以是非常接近
0°,也可以是非常接近180°优质基具有的特点:
- 长度差异非常小:基向量的长度都大概差不多
- 基向量夹角接近正交:基向量之间的夹角接近
90°
- 给出一个图所示:
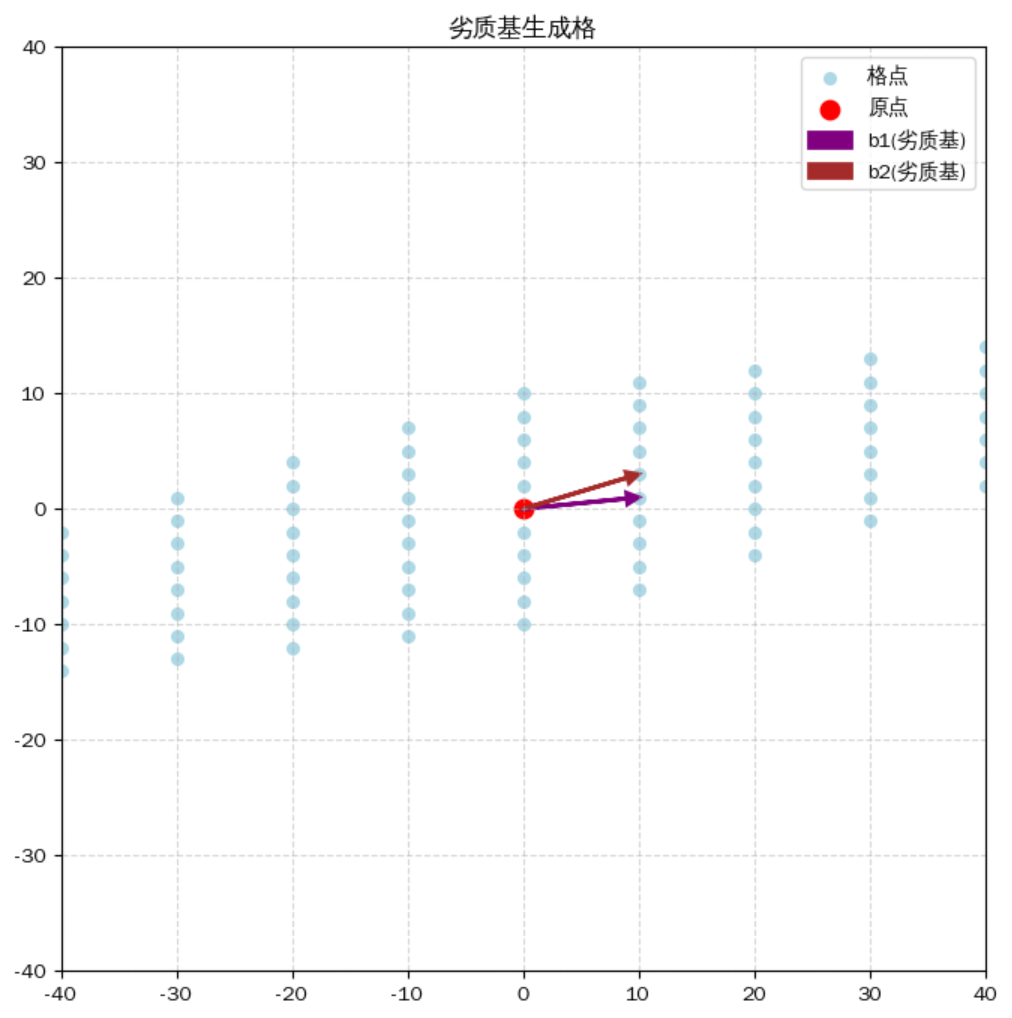
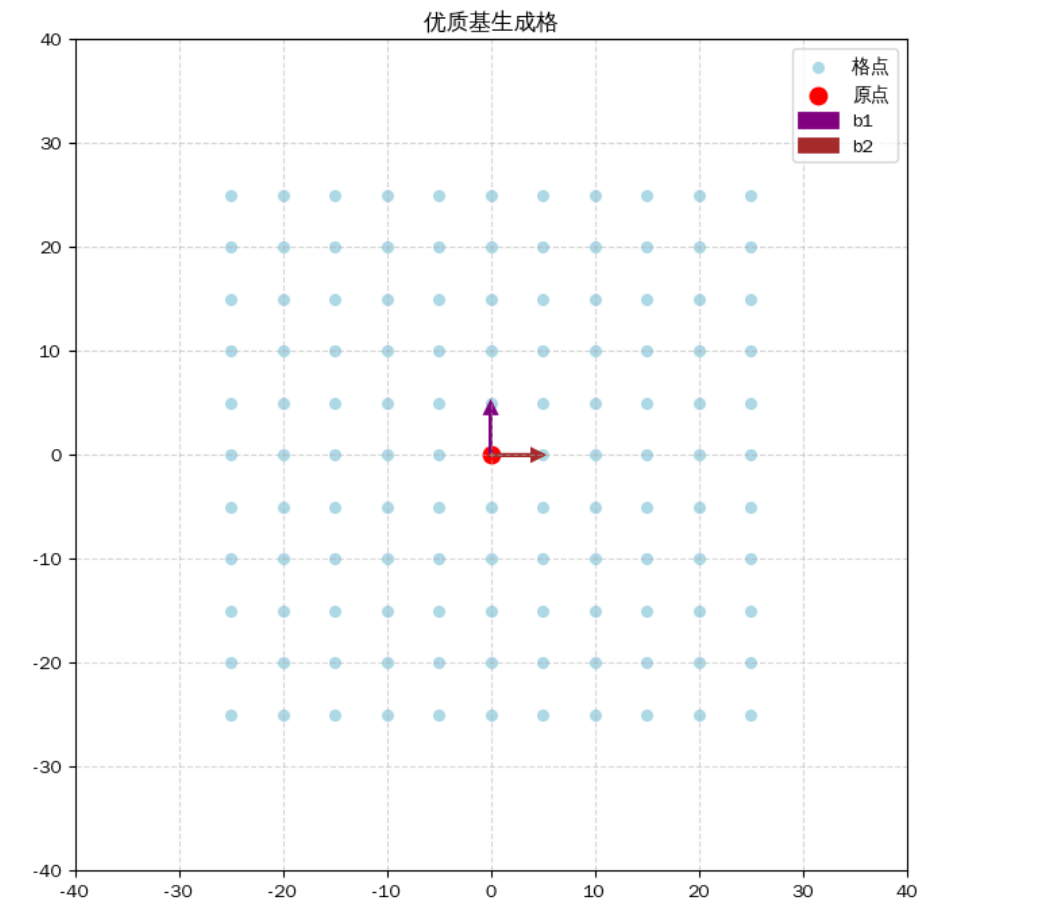
- 优质基生成的格,最典型的优质基其实就是正交向量
格基规约
- 格基规约其实又被称为格基减约,它的英文称为
Lattice Basis Reduction,这里就先简单了解一下格基规约的一个概念。
格基规约,都出现了
格基了,那么肯定是对表示格的基向量做的操作。由于之前已经有说明了,一个格可以使用不同的基表示。而基有优质基和劣质基之分。那么给定一个劣质基表示的格,其实可以通过某种方法将该格使用优质基表示。所以格基规约做了这么一件事情:将劣质基转换为优质基,并且俩个基表示的仍然是同一个格,这个操作就被称为格基规约。
注解:对于格基规约来说,目前有俩个比较著名的算法即:LLL算法 Lenstra–Lenstra–Lovász lattice basis reduction,BKZ算法 Block Korkine-Zolotarev lattice reduction
范数(距离)
- 范数其实就指的是距离,从初一开始接触绝对值,一直到学了勾股定理之后得到了求平面直角坐标系两点之间的距离的方法。这其实就是最经典的
欧几里得距离。对于后面所说的向量长度、距离等指的一般都是欧几里得距离
- 然后到高中一些奇奇怪怪的题,接触到了曼哈顿距离:
- 到了大学,在学习线性代数或者高等代数的时候,给距离取了一个新的名称
范数英文名称为norm,并且给距离下了一个比较统一的定义:
- 对于曼哈顿距离,其实就是
p=1的情况:
- 对于欧几里得距离
欧几里得范数,其实就是p=2的情况:
- 还有一种极限的情况如公式如下所示:
格与群、线性空间
首选来回顾一些格的定义,再介绍一下关于格的另一个定义:
-
定义1:格是中一类具有周期性结构的离散点的集合,严格地来说,格是m维欧式空间的个线性无关向量组的所有整系数线性组合。
-
定义2:格是上的一个离散子群。
从定义中我们可以看出,格这个东西是一个子群,并且与线性空间关系比较大(但是格不是线性空间这一代数结构)所以我们研究线性空间在一定程度上还是对格的学习有帮助的,我们研究抽象的子群的结论也可以用在研究格上。
更正:格并不满足线性空间这个代数结构,之前对格的理解有误,但是它与线性空间有关系
格的基本问题
最短向量问题(SVP)
最短向量问题
Short Vector Problem,SVP:给定格,找一个非零格向量,满足对任意非零向量,有。注解1:是给定一个格找它的最短向量,而不是给定一组基向量找它的最短向量,只不过我们使用一组基向量来描述整个格。
注解2:最短向量问题所描述的找一个
非零格向量,这个向量有特地说明是格向量(格向量其实就是用基表示出来的,在图中其实就是格点)。也就是说,我们需要寻找的就是给定格中的一个点(也就是格向量),使得对于其他格的向量来说满足。注解3:有时候最短向量不唯一,可能有多个。但是最短向量是成对出现的,因为如果找到了一个最短向量,那么它的相反向量其实也是一个最短向量。(如果在具体学习之前有做过比较格密码题目,就会发现有的题格基规约后向量坐标是负数,而正常来说我们解密后的值应该是正数,其实就是因为最短向量一般成对出现)
注解4:对于一组优质基,该基向量中的其中一个向量很可能就是一个最短向量。对于一组劣质基,该基向量中的一个向量大概率都不是最短向量
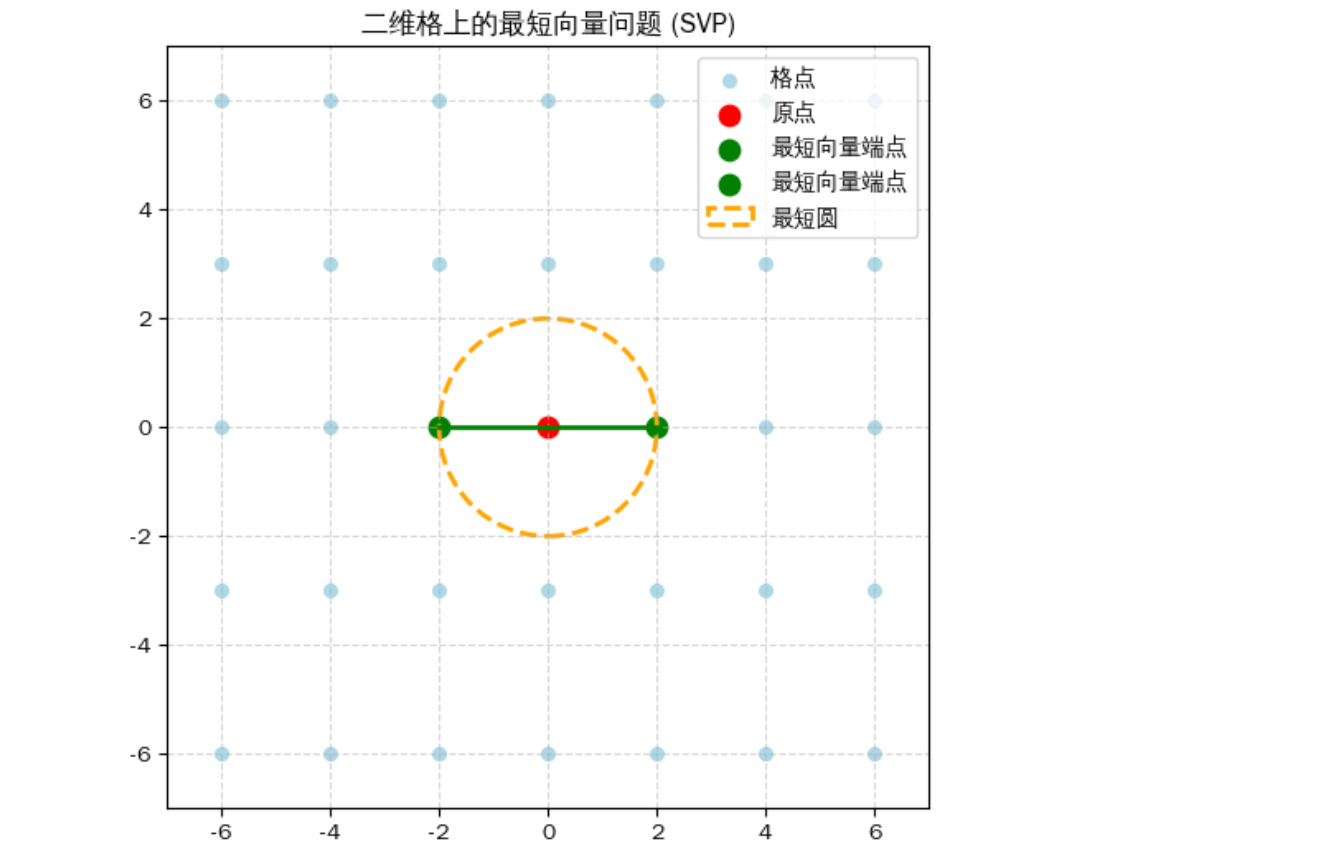
几何理解:这里直接给出二维的平面图来说明,SVP在二维上可以使用几何来理解。其实就是找到一个格点,以该格点与原点的距离为半径,以原点为圆心,画出一个圆。这个圆满足如下两个条件:
- 该圆的内部除了原点外,不能有其他格点
- 格点要么在该圆的圆外,要么在该圆的圆上,而在圆上的点其实就是我们要找的最短向量。
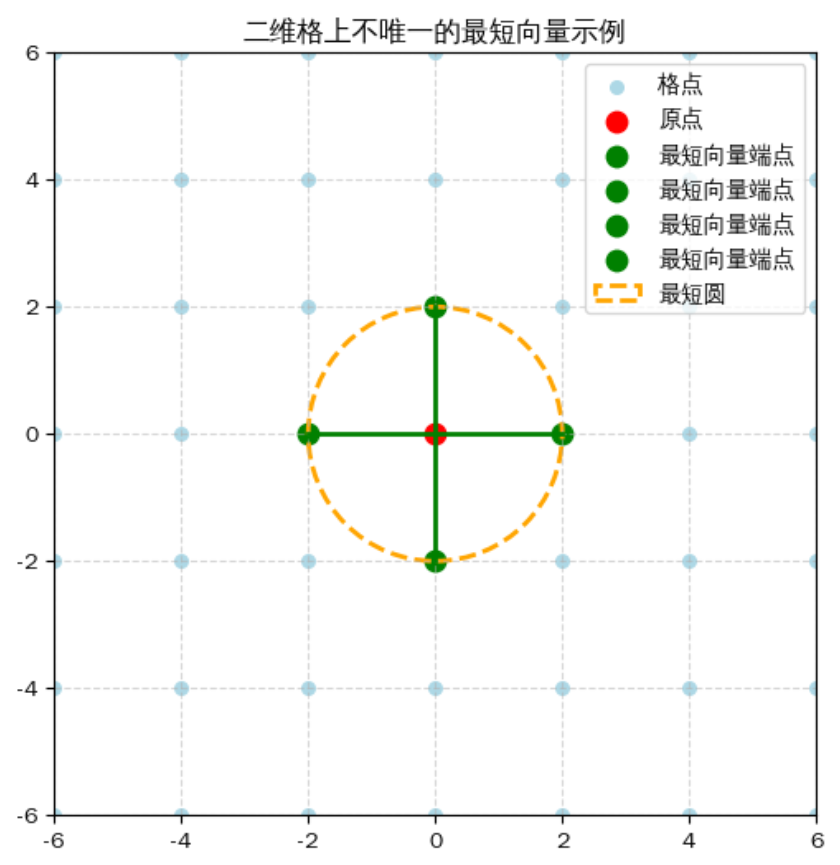
有的时候一个格的最短向量并不唯一,在图中一般最短向量都是关于x轴或者关于y轴对称的。
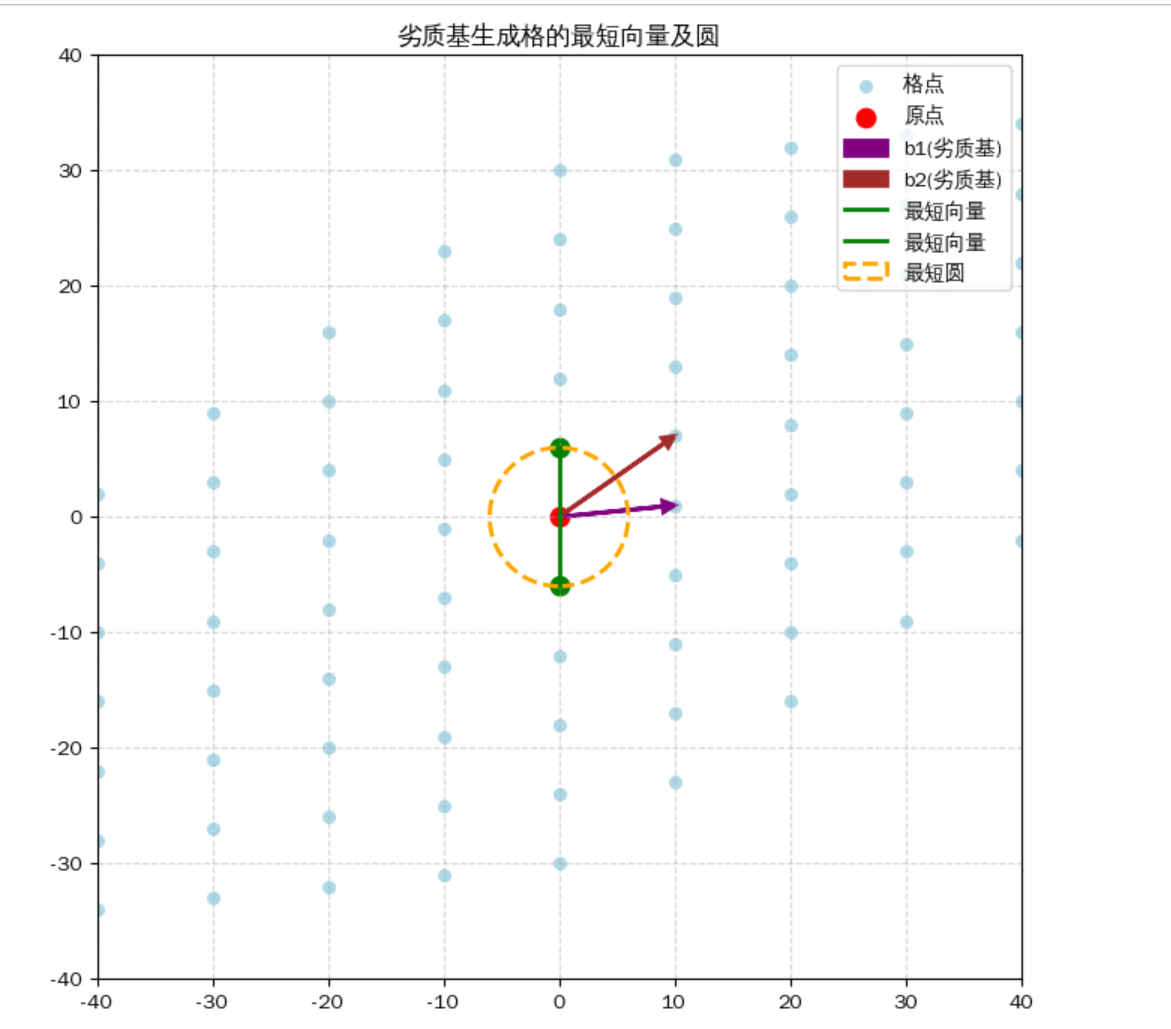
- 下面这个是劣质基寻找最短向量的一个例图
类比:个人感觉找最短向量问题有点和寻找模意义下的指数有点像。(好像更准确的来说是寻找模意义下给定一个底数,求这个底数的模幂运算的阶?)
最近向量问题(CVP)
最近向量问题
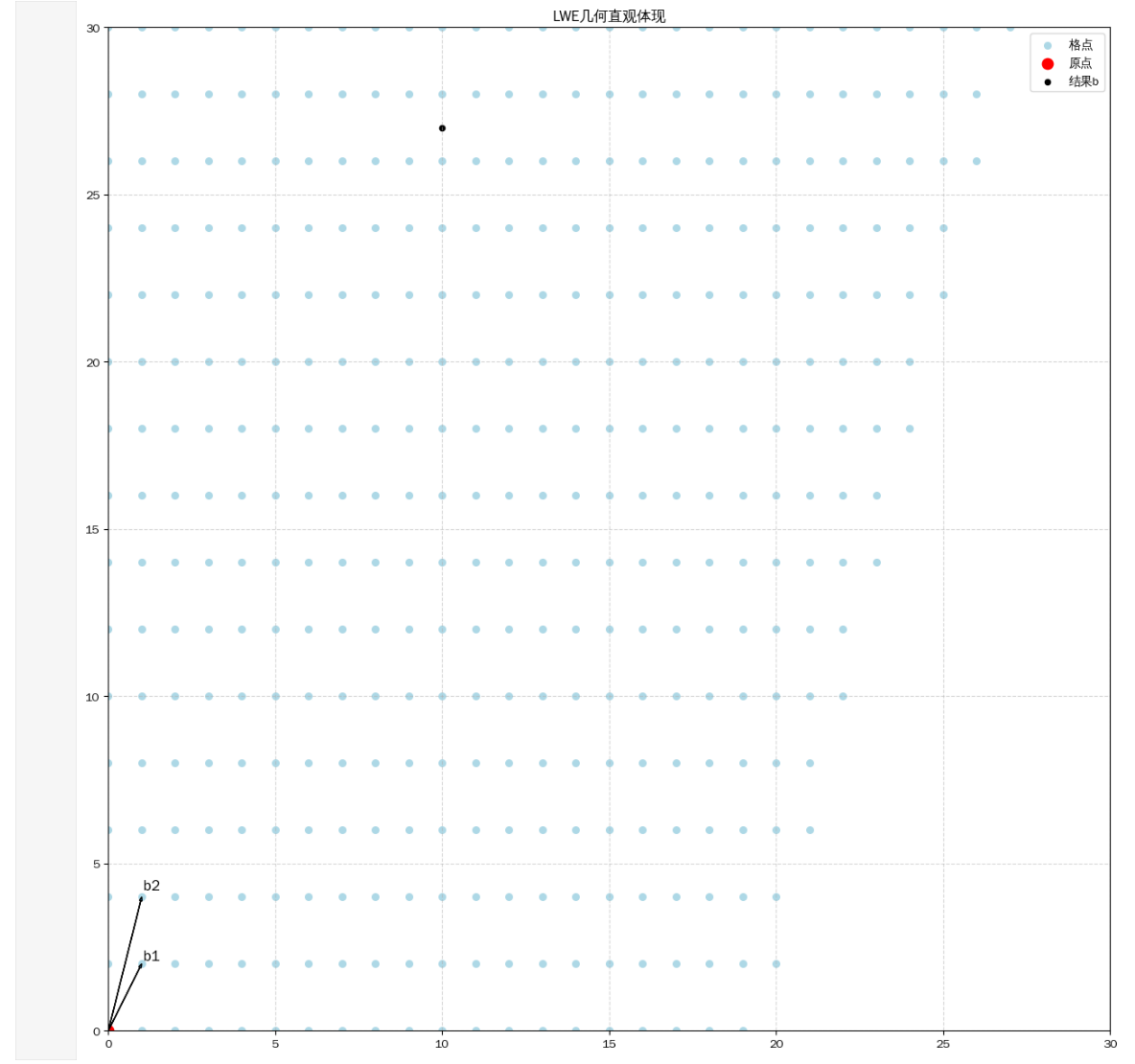
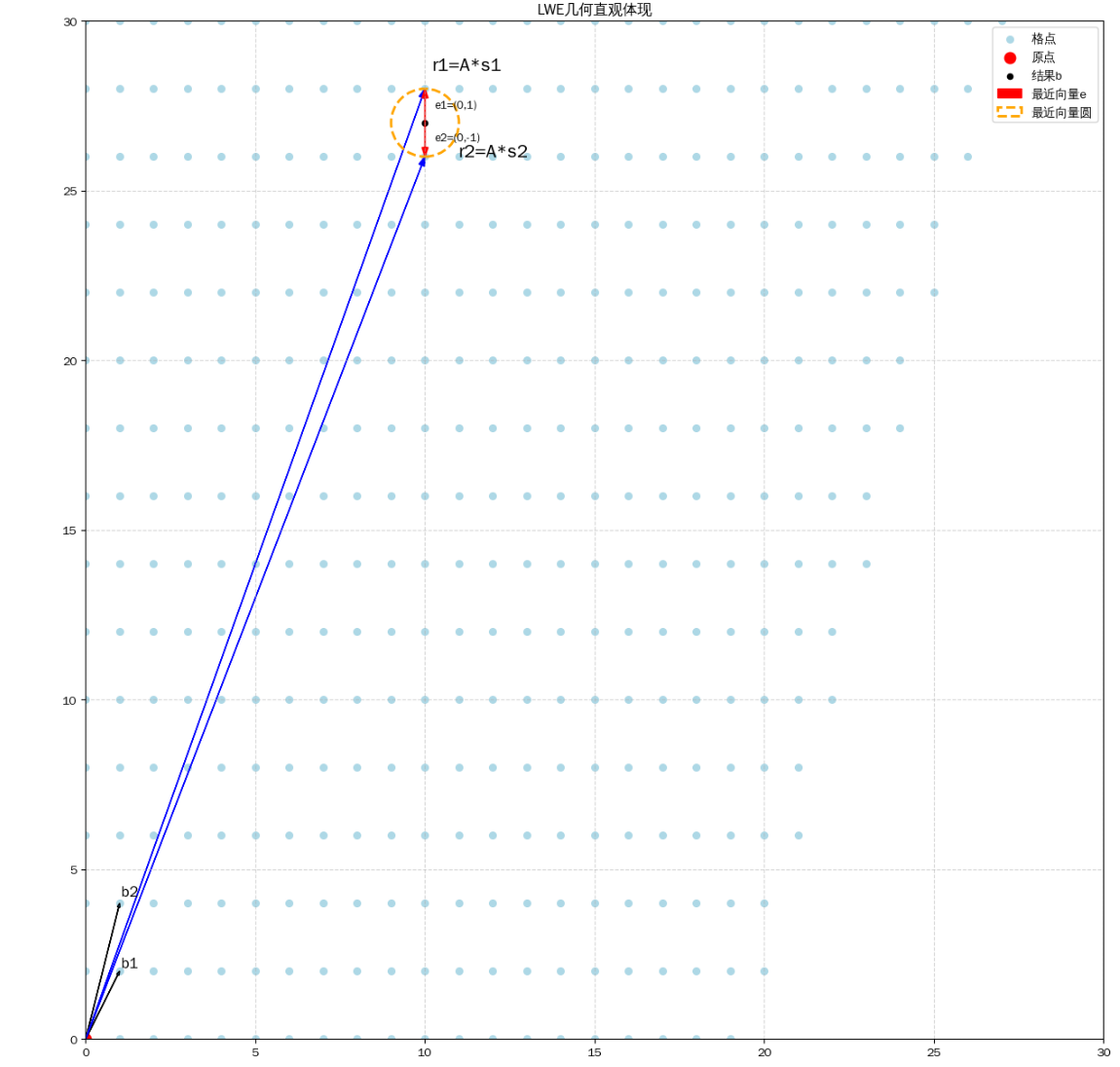
The Closest Vector Problem,CVP:给定格以及一个不在格点上的向量,找一个向量,使得最小。如下图所示(这里偷点小懒把学习LWE问题的最短向量图片直接拿过来用了):
Hermite定理
- 这里主要介绍一下该定理,对应这个定理来说有了前面的知识铺垫应该会比较好理解。对于其他格的定理还有:闵可夫斯基第一定理、界定最短向量长度、闵可夫斯基第二定理、Blichfeldt定理
Hermite定理:
每一个n维的格,都包含一个非零向量,该向量满足
注解1:Hermite定理说明了格中最短向量的一个上界,如果我们遍历到格上的一个向量,如果这个向量可以直接得到这个向量一定不是最短向量。
注解2:Hermite定理缩小了SVP问题遍历格点的范围。
正交基与斯密特正交化
这部分不是讲格的向量,而是讲实数上的向量
正交基
正交基:
对于向量空间的一个基,任意两个不同向量之间的内积为零:,则我们称这个基为正交基
单位正交基
对于一个正交基来说,所有基向量,那么就称该正交基为单位正交基
注解:对于正交基来说,在几何空间中直观的体现就是向量之间两两相互垂直。可以想到高中学的单位正交基。
线性空间中的基本来就是可以用来表示该空间中的任意一个元素,但是还不够好,所以我们就引入了正交基和单位正交基来表示空间中的任意一个元素。使用正交基和单位正交基表示空间中的任意一个元素有如下好处:
以三维几何空间为例子,向量这个是我们在学空间向量中非常熟悉的基底。并且有一个向量,
处理两向量点乘:
- 对于使用正交基表示的向量来说,在计算两向量的点乘时,不需要再花时间计算这样两个不同基向量点乘,因为结果都是0
- 对于使用单位正交基表示的向量来说,在计算两向量点乘时,还可以不需要先计算的值,直接使用对应坐标相乘就行。
总结:所以引入正交基是为了更方便后续的定量计算等,也会提高某些算法的效率。(就像劣质基转换为优质基一样,这种简化的思想在后续解决CVP问题的
baibai算法也有遇到,baibai算法输入优质基可以得到比较精确的最短向量结果)
斯密特正交化
知道了正交基的重要性之后,那就需要研究给定一组任意的一个基,能不能通过一些计算将这个基转换为正交基,这就出现了斯密特正交化。
斯密特正交化:
给定一个基(可能是正交基,也可能不是正交基),将该基转化成一个正交基。如果需要转换成单位正交基,还需要对该正交基进行归一化处理。(目前还没太理解斯密特正交化的过程,等高代学到那边再使用图片来描述一下这个过程,先鸽一下。)
下面就给出
crypto_hack上关于斯密特正交化的伪代码:
- 这里也附上我自己写的斯密特正交化的代码:
1 | def vec_multi(u1:list,v1:list): |
格相关算法
- 提起格相关算法,很多人只知道
LLL算法和BKZ算法这两个算法是格基规约算法,其实他们是基础算法(是解决SVP、CVP问题首先要做的准备),其实格基规约算法也可以近似求解SVP问题。 - 对于解决格中困难问题的算法,为了提高计算效率以及准确性,很多算法都是将优质基作为算法的输入。所以我们在调用算法解决格中困难问题时,我们先要使用格基规约算法将劣质基转换成优质基。将优质基作为相关算法的输入,这样才能提高算法的效率。举一个例子:假设我们要使用
Babai 的 nearest-plane 算法,我们先要使用LLL算法将劣质基转换成优质基,再将优质基作为nearest-plane 算法的输入。去求解问题,求出的解虽然不是精确解,当确是良好近似解。 - 这里我们只是初步学习格相关算法,所以只简单学习两个格相关的算法
LLL算法和Baibai算法。 - 所以我将格相关算法做一个分类,该分类如下图所示:
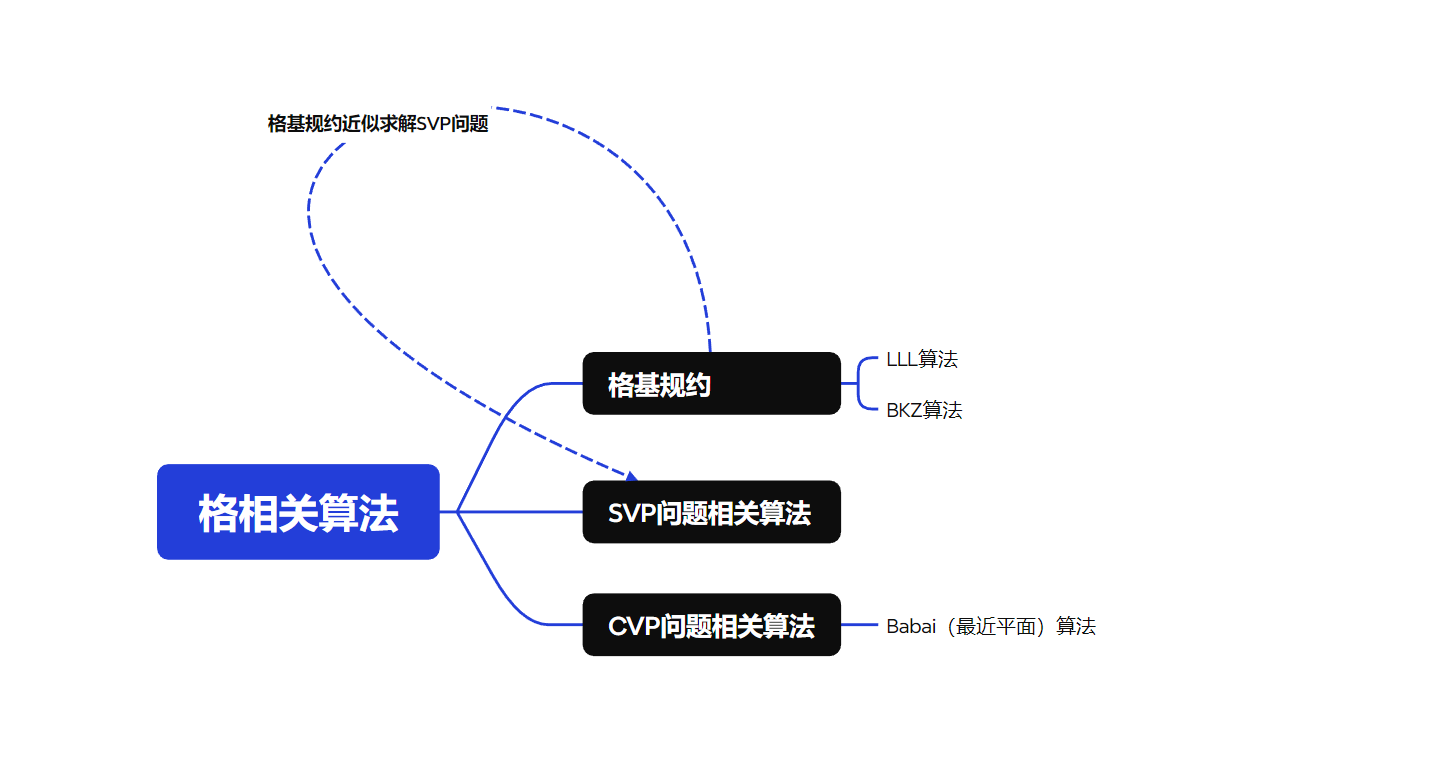
高斯规约算法
- 高斯算法其实可以精确求得二维格上的最短向量,该算法其实是
LLL算法的特殊情况(即LLL算法在二维格上的体现),为了学习LLL算法,先从其特殊情况进行引入。 - 在理解高斯规约算法的时候可以类比欧几里得算法求解最大公约数:
- 欧几里得算法使用辗转相除法,当余数是
0时对应的这个除数就是最大公约数。 - 高斯规约算法使用类似思想,当一个向量在另一个向量上的投影为
0或者四舍五入后为0,基本上满足格基规约的要求。
- 欧几里得算法使用辗转相除法,当余数是
CryptoHack – Lattices challenges
高斯算法的伪代码如下,该伪代码来源于
Jeffrey Hoffstein、Jill Pipher、Joseph H. Silverman写的这本《An Introduction to Mathematical Cryptography》
- 这里也直接贴上高斯规约算法使用Python实现的代码:
1 | def vec_multi(u1:list,v1:list): |
LLL算法
-
其实
高斯规约算法就是LLL算法的一种特殊情况,也就是在维度d=2的这么一个情况。LLL算法将高斯算法拓展到了n维格空间中。 -
LLL算法这个算法的命名其实就是发明它的三个科学家的人名首字母,也就是Arjen Lenstra、Hendrik Willem Lenstra、László Lovász,他们三个共同发表了一篇名为《Lenstra–Lenstra–Lovász: Factoring polynomials with rational coefficients》的论文。 -
具体的论文链接如下:art.pdf
Baibai算法
Baibai算法是应用于解决CVP问题的。该算法是数学家László Babai提出的。- 该算法是在这篇论文中有详细的说明:
《On Lovász’ lattice reduction and the nearest lattice point problem》
格密码相关问题
小整数解问题(SIS问题)
容错学习(LWE问题)
隐藏数问题(HNP)
NTRU问题
近似公约数问题(AGCD)
子集和问题(SSP)
隐藏子集和问题(HSSP)
其余格的问题
r-近似最短向量问题(r-SVP)
逐次最小长度问题(SMP)
最短线性无关向量问题(SIVP)
唯一最短向量问题(uSVP-r)
有界距离解码问题(BDD-r)
判断版本r-近似最短问题(GapSVP-r)
有限距离解码问题(BDD)
BDD英文全称为
Bounded Distance Decoding